1.插入排序
1.1 基本思想
直接插入排序是一种简单的插入排序法，其基本思想是：
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列 。
/**
* 时间复杂度：
* 最好情况：数据完全有序的时候 1 2 3 4 5 ：O(N)
* 最坏情况：数据完全逆序的时候 5 4 3 2 1 ：O(N^2)
* 结论：当所给的数据 越有序 排序 越快。
* 场景：现在有一组基本有序的数据，那么你用哪个排序好点？
*
* 空间复杂度：O(1)
* 稳定性：稳定的排序
* 一个本身就是稳定的排序 是可以实现为不稳定的排序的
* 但是相反 一个本身就不稳定的排序 是不可能实现为稳定的排序的
* @param array
*/
public static void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int tmp = array[i];
int j = i-1;
for (; j >= 0 ; j--) {
if(array[j] > tmp) {
array[j+1] = array[j];
}else {
//array[j+1] = tmp;
break;
}
}
array[j+1] = tmp;
}
}2.希尔排序（缩小增量排序）
希尔排序法又称缩小增量法。希尔排序法的基本思想是：
先选定一个整数，把待排序文件中所有记录分成多个组，
所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，取，重复上述分组和排序的工作。当到达
=1
时，所有记录在统一组内排好序
。
轮着进行插入排序
希尔排序的特性总结：1. 希尔排序是对直接插入排序的优化。2. 当 gap > 1 时都是预排序，目的是让数组更接近于有序。当 gap == 1 时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。3. 希尔排序的时间复杂度不好计算，因为 gap 的取值方法很多，导致很难去计算，因此在好些树中给出的希尔排 序的时间复杂度都不固定。4. 稳定性：不稳定
/**
* 时间复杂度：
* n^1.3 - n^1.5
* 复杂度：O(1)
*
* 稳定性：不稳定的排序
* @param array
*/
public static void shellSort(int[] array) {
int gap = array.length;
while (gap > 1) {
gap /= 2;
shell(array,gap);
}
//shell(array,gap);
}
//这一部分就是插入排序，只是1换为gap
private static void shell(int[] array,int gap) {
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i-gap;
for (; j >= 0 ; j-=gap) {
if(array[j] > tmp) {
array[j+gap] = array[j];
}else {
break;
}
}
array[j+gap] = tmp;
}
}3.选择排序
3.1 基本思想
每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完 。
3.1.1 直接选择排序
/**
* 选择排序：
* 时间复杂度：不管最好还是最坏 都是O(n^2)
* 空间复杂度：O(1)
* 稳定性：不稳定的排序
* @param array
*/
public static void selectSort(int[] array) {
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i+1; j < array.length; j++) {
if(array[j] < array[minIndex]) {
minIndex = j;
}
}
swap(array,minIndex,i);
}
}
private static void swap(int[] array,int i,int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}public static void selectSort2(int[] array) {
int left = 0;
int right = array.length-1;
while (left < right) {
int minIndex = left;
int maxIndex = left;
for (int i = left+1; i <= right ; i++) {
if(array[i] < array[minIndex]) {
minIndex = i;
}
if(array[i] > array[maxIndex]) {
maxIndex = i;
}
}
swap(array,left,minIndex);
//最大值刚好 在最小值的位置 已经交换到了minIndex
if(maxIndex == left) {
maxIndex = minIndex;
}
swap(array,right,maxIndex);
left++;
right--;
}//最大值刚好 在最小值的位置 已经交换到了minIndex
3.1.2 堆排序
1.堆排序
堆排序即利用堆的思想来进行排序，总共分为两个步骤：
1. 建堆
升序：建大堆
降序：建小堆
2. 利用堆删除思想来进行排序
建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。
1.调整为大根堆
2.让第一个元素 和 最后一个未排序的元素进行交换
public void heapSort() {
int end = usedSize-1;
while (end > 0) {
swap(0,end);
shiftDown(0,end);
end--;
}
}/**
* 时间复杂度：
* O(n*logN) N^1.3 -->
* 空间复杂度：O(1)
* 稳定性：不稳定的
* 数据量非常 大的时候 堆排 一定比希尔快
* @param array
*/
public static void heapSort(int[] array) {
createBigHeap(array);
int end = array.length-1;
while (end > 0) {
swap(array,0,end);
siftDown(array,0,end);
end--;
}
}
private static void createBigHeap(int[] array) {
for (int parent = (array.length-1-1)/2; parent >= 0 ; parent--) {
siftDown(array,parent,array.length);
}
}
private static void siftDown(int[] array,int parent,int end) {
int child = 2*parent+1;
while (child < end) {
if(child + 1 < end && array[child] < array[child+1]) {
child++;
}
if(array[child] > array[parent]) {
swap(array,child,parent);
parent = child;
child = 2*parent+1;
}else {
break;
}
}
}4.交换排序
4.1 冒泡排序
【
冒泡排序的特性总结
】
1.
冒泡排序是一种非常容易理解的排序
2.
时间复杂度：
O(N^2)
3.
空间复杂度：
O(1)
4.
稳定性：稳定
/**
* 冒泡排序：
* 时间复杂度： o(n^2) 如果加了优化 最好情况O(N)
* 空间复杂度：O(1)
* 稳定性：稳定的排序
* @param array
*/
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length-1; i++) {
boolean flg = false;
for (int j = 0; j < array.length-1-i; j++) {
if(array[j] > array[j+1]) {
swap(array,j,j+1);
flg = true;
}
}
if(!flg) {
return;
}
}
}4.2 快速排序
4.2.1 Hoare法
快速排序是
Hoare
于
1962
年提出的一种二叉树结构的交换排序方法，其基本思想为：
任取待排序元素序列中的某元
素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有
元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止
。
找基准
//二叉树递归的过程
/** * 时间复杂度： * 最好情况: * O(N*logN) 满二叉树/完全二叉树 * 最坏情况: * O(N^2) 单分支的树 * 空间复杂度： * 最好情况: * O(logN) 满二叉树/完全二叉树 * 最坏情况: * O(N) 单 分支的树 * 稳定性：不稳定 * @param array */ public static void quickSort(int[] array) { quick(array,0,array.length-1); } private static void quick(int[] array,int start,int end) { if(start >= end) return;//左边是一个节点 或者 连一个节点都没有 if(end - start + 1 <= 7) { //插入排序 insertSortRange(array,start,end); return; } //三数取中 int index = midOfThree(array,start,end); swap(array,index, start);//此时交换完成之后 一定能过保证start下标 是中间大的数字 int pivot = partition(array,start,end); quick(array,start,pivot-1); quick(array,pivot+1,end); } private static int partitionHoare(int[] array,int left,int right) { int key = array[left]; int i = left; while (left < right) { while (left < right && array[right] >= key) {//这里为什么要取等号 right--; } //right 下标一定是 比key小的数据 while (left < right && array[left] <= key) {//这里为什么要取等号 left++; } //left 下标一定是 比key大的数据 swap(array,left,right); } //相遇的位置 和 i 位置进行交换 swap(array,left,i); return left; }//必须要right先走
4.2.2 挖坑法
private static int partition(int[] array,int left,int right) {
int key = array[left];
while (left < right) {
while (left < right && array[right] >= key) {//这里为什么要取等号
right--;
}
//right 下标一定是 比key小的数据
array[left] = array[right];
while (left < right && array[left] <= key) {//这里为什么要取等号
left++;
}
//left 下标一定是 比key大的数据
array[right] = array[left];
}
array[left] = key;
return left;
}4.2.3 前后指针
/**
* 时间复杂度：
* 最好情况:
* O(N*logN) 满二叉树/完全二叉树
* 最坏情况:
* O(N^2) 单分支的树
* 空间复杂度：
* 最好情况:
* O(logN) 满二叉树/完全二叉树
* 最坏情况:
* O(N) 单 分支的树
* 稳定性：不稳定
* @param array
*/
public static void quickSort(int[] array) {
quick(array,0,array.length-1);
}
private static void quick(int[] array,int start,int end) {
if(start >= end) return;//左边是一个节点 或者 连一个节点都没有
if(end - start + 1 <= 7) {
//插入排序
insertSortRange(array,start,end);
return;
}
//三数取中
int index = midOfThree(array,start,end);
swap(array,index, start);//此时交换完成之后 一定能过保证start下标 是中间大的数字
int pivot = partition(array,start,end);
quick(array,start,pivot-1);
quick(array,pivot+1,end);
}
private static void insertSortRange(int[] array,int begin,int end) {
for (int i = begin+1; i <= end; i++) {
int tmp = array[i];
int j = i-1;
for (; j >= begin ; j--) {
if(array[j] > tmp) {
array[j+1] = array[j];
}else {
break;
}
}
array[j+1] = tmp;
}
}
private static int midOfThree(int[] array, int left, int right) {
int mid = (left+right) / 2;
if(array[left] < array[right]) {
if(array[mid] < array[left]) {
return left;
}else if(array[mid] > array[right]) {
return right;
}else {
return mid;
}
}else {
if(array[mid] > array[left]) {
return left;
}else if(array[mid] < array[right]) {
return right;
}else {
return mid;
}
}
}
private static int partitionHoare(int[] array,int left,int right) {
int key = array[left];
int i = left;
while (left < right) {
while (left < right && array[right] >= key) {//这里为什么要取等号
right--;
}
//right 下标一定是 比key小的数据
while (left < right && array[left] <= key) {//这里为什么要取等号
left++;
}
//left 下标一定是 比key大的数据
swap(array,left,right);
}
//相遇的位置 和 i 位置进行交换
swap(array,left,i);
return left;
}
private static int partition(int[] array,int left,int right) {
int key = array[left];
while (left < right) {
while (left < right && array[right] >= key) {//这里为什么要取等号
right--;
}
//right 下标一定是 比key小的数据
array[left] = array[right];
while (left < right && array[left] <= key) {//这里为什么要取等号
left++;
}
//left 下标一定是 比key大的数据
array[right] = array[left];
}
array[left] = key;
return left;
}
private static int partition3(int[] array, int left, int right) {
int prev = left ;
int cur = left+1;
while (cur <= right) {
if(array[cur] < array[left] && array[++prev] != array[cur]) {
swap(array,cur,prev);
}
cur++;
}
swap(array,prev,left);
return prev;
}
public static void quickSortNor(int[] array) {
Stack<Integer> stack = new Stack<>();
int left = 0;
int right = array.length-1;
int piovt = partition(array,left,right);
if(piovt - 1 > left) {
stack.push(left);
stack.push(piovt-1);
}
if(piovt + 1 < right) {
stack.push(piovt+1);
stack.push(right);
}
while (!stack.isEmpty()) {
right = stack.pop();
left = stack.pop();
piovt = partition(array,left,right);
if(piovt - 1 > left) {
stack.push(left);
stack.push(piovt-1);
}
if(piovt + 1 < right) {
stack.push(piovt+1);
stack.push(right);
}
}
}5.归并排序
5.1 基本思想
归并排序（MERGE-SORT
）是建立在归并操作上的一种有效的排序算法
,
该算法是采用分治法（
Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤：
/**
* 时间复杂度： 0(N*logN)
* 空间复杂度：O(n)
* 稳定性: 稳定
* 插入排序 冒泡 归并
* @param array
*/
public static void mergeSort(int[] array) {
mergeSortFunc(array,0,array.length-1);
}
private static void mergeSortFunc(int[] array,int left,int right) {
if(left >= right) return;
int mid = (left+right) / 2;
mergeSortFunc(array,left,mid);
mergeSortFunc(array,mid+1,right);
merge(array,left,right,mid);
}
private static void merge(int[] array, int left, int right, int mid) {
int s1 = left;
int s2 = mid+1;
int[] tmpArr = new int[right-left+1];
int k = 0;
//证明两个区间 都同时有数据的
while (s1 <= mid && s2 <= right) {
if(array[s2] <= array[s1]) {
tmpArr[k++] = array[s2++];
}else {
tmpArr[k++] = array[s1++];
}
}
while (s1 <= mid) {
tmpArr[k++] = array[s1++];
}
while (s2 <= right) {
tmpArr[k++] = array[s2++];
}
//tmpArr 里面一定是这个区间内有序的数据了
for (int i = 0; i < tmpArr.length; i++) {
array[i+left] = tmpArr[i];
}
}
public static void mergeSortNor(int[] array) {
int gap = 1;
while (gap < array.length) {
for (int i = 0; i < array.length; i += 2*gap) {
int left = i;
int mid =left+gap-1;
int right = mid+gap;
if(mid >= array.length) {
mid = array.length-1;
}
if(right >= array.length) {
right = array.length-1;
}
merge(array,left,right,mid);
}
gap *= 2;
}
}5.2 归并排序总结
1. 归并的缺点在于需要
O(N)
的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。
2.
时间复杂度：
O(N*logN)
3.
空间复杂度：
O(N)
4.
稳定性：稳定
6.其他非基于比较排序
6.1 基数排序
1.10 基数排序 | 菜鸟教程
6.2 桶排序
【排序】图解桶排序_桶排序图解-CSDN博客
6.3 计数排序
/**
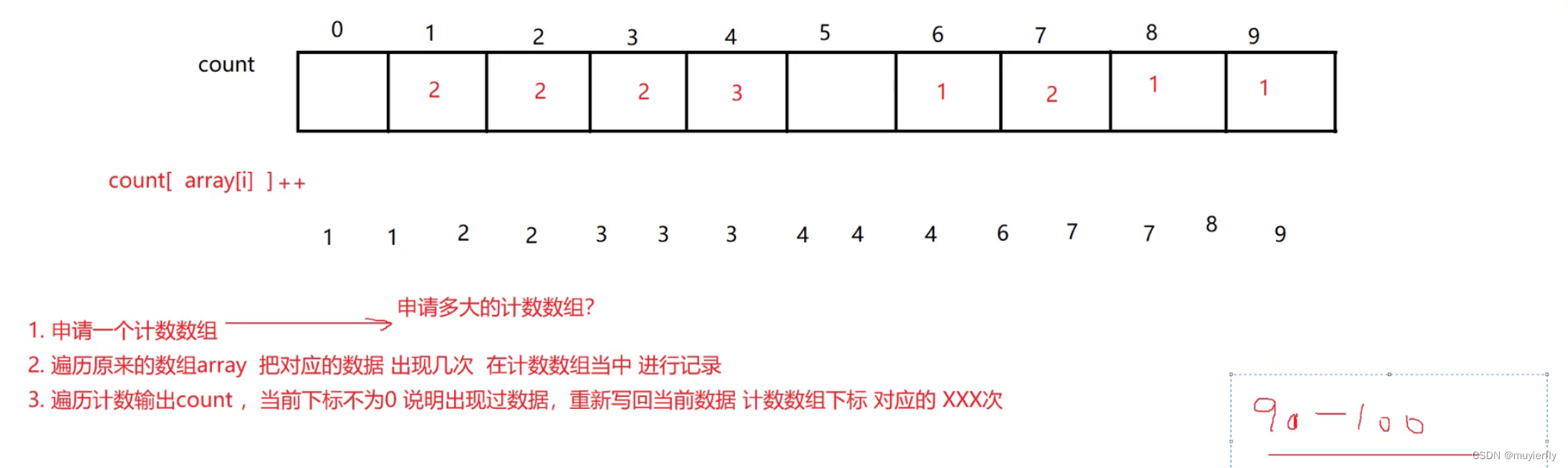
* 时间复杂度：
* O(N+范围)
* 空间复杂度：O(范围)
* 稳定性：
*
* 计数排序 和 你给定的 范围有关系
* @param array
*/
public static void countSort(int[] array) {
int minVal = array[0];
int maxVal = array[0];
//1、求当前数组的最大值 和 最小值
for (int i = 1; i < array.length; i++) {
if(array[i] < minVal) {
minVal = array[i];
}
if(array[i] > maxVal) {
maxVal = array[i];
}
}
//2.跟进最大值 和 最小值 来确定数组的大小
int[] count = new int[maxVal-minVal+1];
//3、遍历原来的数组 开始计数
for (int i = 0; i < array.length; i++) {
count[array[i]-minVal]++;
}
//4、遍历计数cout 把 当前元素 写回 array
int index = 0;//重新表示array数组的下标
for (int i = 0; i < count.length; i++) {
while (count[i] > 0) {
array[index] = i+minVal;
index++;
count[i]--;
}
}
}
