栈与递归的实现

1. 栈的概念及结构

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。

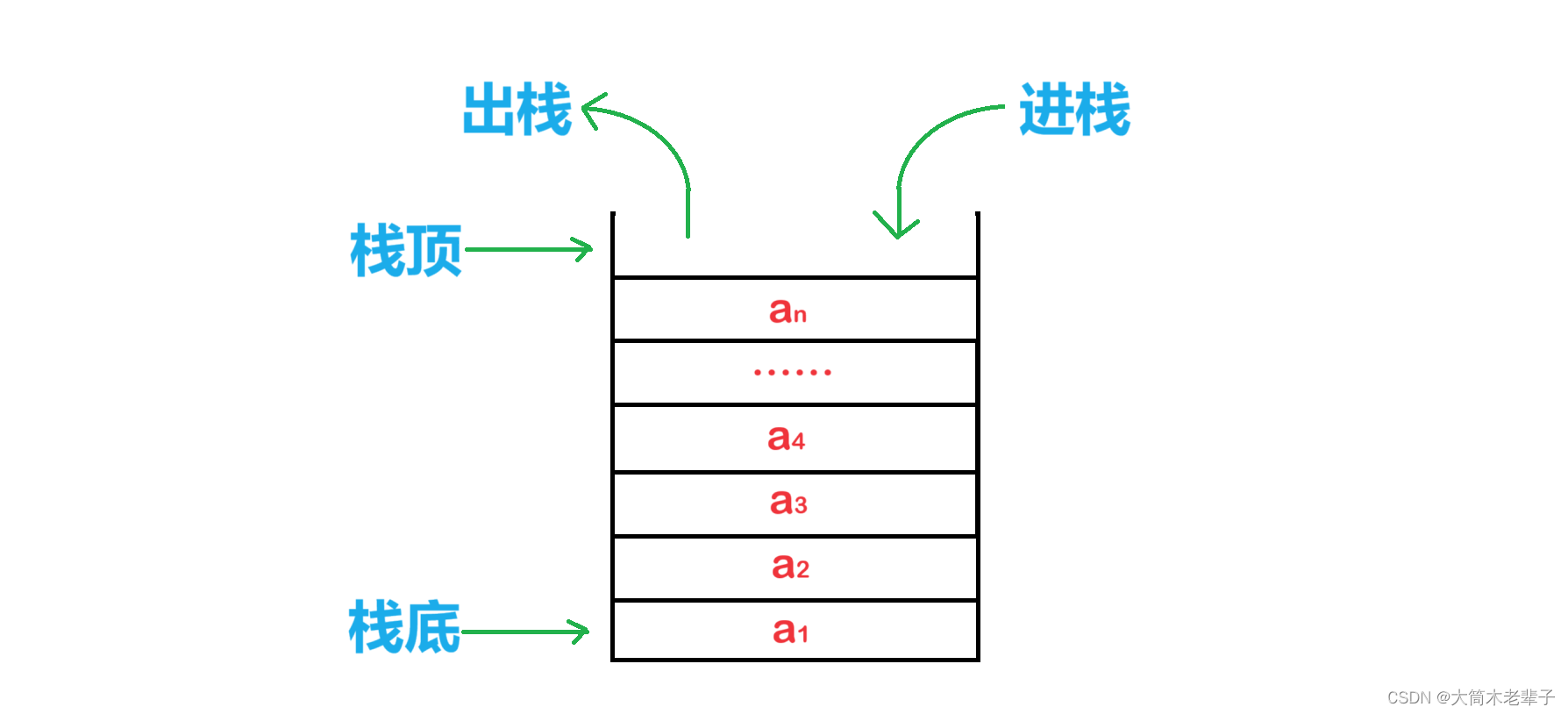
进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。

栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则，因此栈又被称作后进先出的线性表。

压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。

出栈：栈的删除操作叫做出栈。出数据也在栈顶。

根据上述定义，每次进栈的元素都被放在原栈顶元素之上而成为新的栈顶，而每次出栈的总是当前栈中“最新”的元素，即最后进栈的元素。

在下面栈的结构示意图中，元素是以a1，a2，a3，……，an的顺序进栈的，而出栈的次序却是an，……，a3，a2，a1。

在日常生活中也可以见到很多后进先出的例子，例如：

手枪子弹夹中的子弹，铁路调度站以及函数栈帧的创建与销毁等……

栈的基本操作除了进栈（栈顶插入），出栈（删除栈顶元素）外，还有建立栈（栈的初始化），判空，获取栈中数据个数以及取栈顶元素等。

2. 栈的实现

栈作为一种特殊的线性表，在计算机中主要有两种基本的存储结构：顺序存储结构和链式存储结构。

采用顺序存储结构的栈简称顺序栈，采用链式存储结构的栈简称为链栈。

相比之下，顺序栈要比链栈更优，因为顺序栈在尾上插入数据的代价较小。

结构与接口函数定义

typedef int STDataType;

typedef struct Stack
{
	STDataType* data;
	int top;
	int capacity;
}Stack;

//初始化
void STInit(Stack* pst);
//销毁
void STDestroy(Stack* pst);
//插入
void STPush(Stack* pst, STDataType x);
//删除
void STPop(Stack* pst);
//获取栈顶数据
STDataType STTop(Stack* pst);
//判断是否为空
bool STEmpty(Stack* pst);
//剩余数据个数
int STSize(Stack* pst);

接口函数的实现

void CheckCapacity(Stack* pst)
{
	assert(pst);
	if (pst->top == pst->capacity)
	{
		int newcapacity = (pst->capacity == 0) ? 4 : (pst->capacity * 2);
		STDataType* tmp = (STDataType*)realloc(pst->data, sizeof(STDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}

		pst->data = tmp;
		pst->capacity = newcapacity;
	}
}

//初始化
void STInit(Stack* pst)
{
	assert(pst);
	pst->data = NULL;
	//top指向栈顶数据的下一个位置
	pst->top = 0;
	pst->capacity = 0;
}

//销毁
void STDestroy(Stack* pst)
{
	assert(pst);
	free(pst->data);
	pst->capacity = 0;
	pst->top = 0;
}

//插入
void STPush(Stack* pst, STDataType x)
{
	assert(pst);
	CheckCapacity(pst);
	pst->data[pst->top++] = x;
}

//删除
void STPop(Stack* pst)
{
	assert(pst);
	if(pst->top > 0)
	pst->top--;
}

//获取栈顶数据
STDataType STTop(Stack* pst)
{
	assert(pst);
	assert(!STEmpty(pst));

	return pst->data[pst->top - 1];
}

//判断是否为空
bool STEmpty(Stack* pst)
{
	assert(pst);
	return pst->top == 0;
}

//剩余数据个数
int STSize(Stack* pst)
{
	assert(pst);
	return pst->top;
}

3. 栈与递归的实现

前面提到，函数栈帧的创建与销毁过程也是以栈这一数据结构为基础的。

而将函数栈帧的创建与销毁利用到极致的便是递归这一解决问题的手段。

递归算法就是在算法中直接或间接调用算法本身的算法。

如果一个函数在其定义体内直接调用自己，则称为直接递归函数；如果一个函数经过一系列的中间调用语句，通过其他函数间接调用自己，则称为间接递归函数。

使用递归算法有以下两个前提：

1. 原问题可以层层分解为类似的子问题，且子问题比原问题的规模小。

2. 规模最小的子问题具有直接解。

设计递归算法的原则是用自身的简单情况来定义自身，方法如下：

1. 寻找分解方法：将原为你转化为子问题求解。例如，n! = n(n-1)!

2. 设计递归出口：根据规模最小的子问题确定递归终止条件。例如，求解n!，当n = 1时，n! = 1。

有许多问题利用递归来解决会十分简单，如快速排序，汉诺塔问题，图的深度优先搜索等。

其递归算法比迭代算法在逻辑上更简明。

可以看出，递归既是强有力的数学方法，也是程序设计中一个很有用的工具。

递归算法具有以下两个特征：

1. 递归算法是一种分而治之，把复杂问题分解为简单问题的问题求解方法，对求解某些复杂问题，递归分析方法是有效的。

2. 递归算法的效率较低。

为此，在求解某些问题时，希望用递归算法分析问题，用非递归算法求解具体问题。

栈非常重要的一个应用就是在程序设计语言中用来实现递归。

3.1 消除递归的原因

（1）有利于提高算法的时空性能，因为递归执行时需要操作系统提供隐式栈来实现递归，所以效率较低。

（2）无应用递归语句的语言设施环境条件，有些计算机语言不支持递归功能，如FORTRAN语言中无递归机制。

（3）递归算法中频繁的函数调用不利于调试与观察。

3.2 递归过程的实现

递归进层(i→i+1层)时系统需要做三件事：

（1）保留本层参数与返回地址。

（2）为被调用函数的局部变量分配存储区,给下层参数赋值。

（3）将程序转移到被调用函数的入口。

而从被调用函数返回调用函数之前,递归退层(i←i+1层)时系统也应完成三件事：

（1）保存被调用函数的计算结果。

（2）释放被调用函数的数据区,恢复上层参数。

（3）依照被调用函数保存的返回地址,将控制转移回调用函数。

当递归函数调用时，应按照“后调用先返回”的原则处理调用过程，因此上述函数之间的信息传递和控制转移必须通过栈来实现。

系统将整个程序运行时所需的数据空间安排在一个栈中，每当调用一个函数时，就为它在栈顶分配一个存储区，而每当从一个函数退出时，就释放它的存储区。

显然，当前正在运行的函数的数据区必在栈顶。

一个递归函数的运行过程中，调用函数和被调用函数是同一个函数，因此,与每次调用相关的一个重要概念就是递归函数运行的“层次”。

假设调用该递归函数的主函数为第0层，则从主函数调用递归函数为进入第1层……从第i层递归调用该函数为进入其“下一层”，即第i+1层；反之，退出第i层递归应返回至其“上一层”，即第i -1层。

为了保证递归函数正确执行，系统需设立一个递归工作栈，作为整个递归函数运行期间使月用的数据存储区。

每层递归所需信息构成一个工作记录，其中包括所有实在参数，所有局部变量以及上一层返回地址。

每进入一层递归，就产生一个新的工作记录压入栈顶；每退出一层递归,就从栈顶弹出一个工作记录。

因此当前执行层的工作记录必为递归工作栈栈顶的工作记录，该记录称为内活动记录，指示活动记录的栈顶指针称为当前环境指针。

由于递归工作栈是由系统来管理的，无须页用户操心，所以用递归法编制程序非常方便。

在理解了递归的机制之后，我们就可以尝试将一些递归算法改写为非递归算法。

接下来，我们以二叉树的遍历算法为例。

3.3 二叉树的遍历算法

3.3.1 递归算法

先序遍历：

//先序遍历的递归算法
void PreOrder1(BTNode* b)
{
    if(b == NULL)
    return;

    //访问根结点
    printf("%d ", b->_data);
    //访问左子树
    PreOrder1(b->_left);
    //访问右子树
    PreOrder1(b->_right);
}

中序遍历：

//中序遍历的递归算法
void MidOrder1(BTNode* b)
{
    if(b == NULL)
    return;

    //访问左子树
    MidOrder1(b->_left);
    //访问根结点
    printf("%d ", b->_data);
    //访问右子树
    MidOrder1(b->_right);
}

后序遍历：

//后序遍历的递归算法
void AftOrder1(BTNode* b)
{
    if(b == NULL)
    return;

    //访问左子树
    AftOrder1(b->_left);
    //访问右子树
    AftOrder1(b->_right);
    //访问根结点
    printf("%d ", b->_data);
}

3.3.2 非递归算法

先序遍历：

//先序遍历的非递归算法1
void PreOrder2(BTNode* b)
{
    Stack st;
    STInit(&st);
    BTNode* p = b;
    if(b != NULL)
    {
        STPush(&st, p);//根结点入栈
        while(!STEmpty(&st))
        {
            p = STTop(&st);
            printf("%d ", p->_data);
            STPop(&st);

            if(p->_right != NULL)
            STPush(&st, p->_right);
            if(p->_left != NULL)
            STPush(&st, p->_left);
        }
    }
    STDestroy(&st);
}

//先序遍历的非递归算法2
void PreOrder3(BTNode* b)
{
    Stack st;
    STInit(&st);
    BTNode* p = b;
    while(!STEmpty(&st) || p != NULL)
    {
        //访问根结点并依次访问左孩子
        while(p != NULL)
        {
            STPush(&st, p);
            printf("%d ", p->_data);
            p = p->_left;
        }
        //退回上一层，找右孩子
        if(!STEmpty(&st))
        {
            p = STTop(&st);
            STPop(&st);
            p = p->_right;
        }
    }
    
    STDestroy(&st);
}

中序遍历：

//中序遍历的非递归算法
void MidOrder2(BTNode* b)
{
    Stack st;
    STInit(&st);
    BTNode* p = b;
    while(!STEmpty(&st) || p != NULL)
    {
        //将p及左孩子依次入栈
        while(p != NULL)
        {
            STPush(&st, p);
            p = p->_left;
        }
        //退回上一层并访问根结点，找右孩子
        if(!STEmpty(&st))
        {
            p = STTop(&st);
            STPop(&st);
            printf("%d ", p->_data);
            p = p->_right;
        }
    }
    STDestroy(&st);
}

后序遍历：

//后序遍历的非递归算法
void AftOrder2(BTNode* b)
{
    Stack st;
    STInit(&st);
    BTNode* p = b;
    BTNode* asked = NULL;//指向刚刚访问过的结点
    bool flag = true;//为真表示正在处理栈顶结点
    do
    {
        //p及左孩子依次进栈
        while(p != NULL)
        {
            STPush(&st, p);
            p = p->_left;
        }
        asked = NULL;
        flag = true;

        while(!STEmpty(&st) && flag)
        {
            p = STTop(&st);
            if(p->_right == asked)//右孩子刚被访问过或者为空
            {
                printf("%d ", p->_data);
                STPop(&st);
                asked = p;
            }
            else
            {
                p = p->_right;
                flag = false;
            }
        }
    } while (!STEmpty(&st));
    
    STDestroy(&st);
}

3.3.3 先序遍历的非递归算法解读

先序遍历2与中序遍历类似，只是访问的时机不同，而后序遍历的非递归算法较为麻烦，这里不做过多解释。

先序遍历1：

//先序遍历的非递归算法1
void PreOrder2(BTNode* b)
{
    Stack st;
    STInit(&st);
    BTNode* p = b;
    if(b != NULL)
    {
        STPush(&st, p);//根结点入栈
        while(!STEmpty(&st))
        {
            p = STTop(&st);
            //访问
            printf("%d ", p->_data);
            STPop(&st);

            if(p->_right != NULL)
            STPush(&st, p->_right);
            if(p->_left != NULL)
            STPush(&st, p->_left);
        }
    }
    STDestroy(&st);
}

当b不为空时，我们首先让根结点入栈。

每次循环，我们都先访问根结点（当前栈顶元素），然后将右孩子与左孩子分别入栈（后进先出，要先访问左子树就要先入右孩子）。

该种算法的思路与递归算法十分类似，然而，解决问题的路径却不相同。

在递归算法中，左子树被全部访问完之后，负责访问右子树的函数才会入栈；而在非递归的算法中，由于语言的限制，我们必须在一次循环中就将左右孩子都入栈，但是依靠栈后进先出的特点，我们可以通过先入右孩子再入左孩子的方式来保证左孩子一定比右孩子先入栈。

这样的思路并不对所有情况成立，比如，这样的思路就很难解决中序遍历。

为此，我们用适用于先序遍历和中序遍历的思路写了先序遍历2算法。

先序遍历2：

//先序遍历的非递归算法2
void PreOrder3(BTNode* b)
{
    Stack st;
    STInit(&st);
    BTNode* p = b;
    while(!STEmpty(&st) || p != NULL)
    {
        //访问根结点并依次访问左孩子
        while(p != NULL)
        {
            STPush(&st, p);
            //访问
            printf("%d ", p->_data);
            p = p->_left;
        }
        //退回上一层，找右孩子
        if(!STEmpty(&st))
        {
            p = STTop(&st);
            STPop(&st);
            p = p->_right;
        }
    }
    
    STDestroy(&st);
}

这种算法的思路就是模拟函数调用的顺序来访问结点。

首先将左孩子（包括根结点）依次入栈并访问，遇到某结点左子树为空，则通过退回上一层（出栈）的方式找到该结点，并将访问的方向转到其右子树。

这种思路解决问题的路径就与递归算法完全一样，若要进行中序遍历，只需要改变访问的时机，具体参考上一模块的有关代码。