用Rust打印杨辉三角

news2024/11/28 9:27:27

一、杨辉三角是什么？

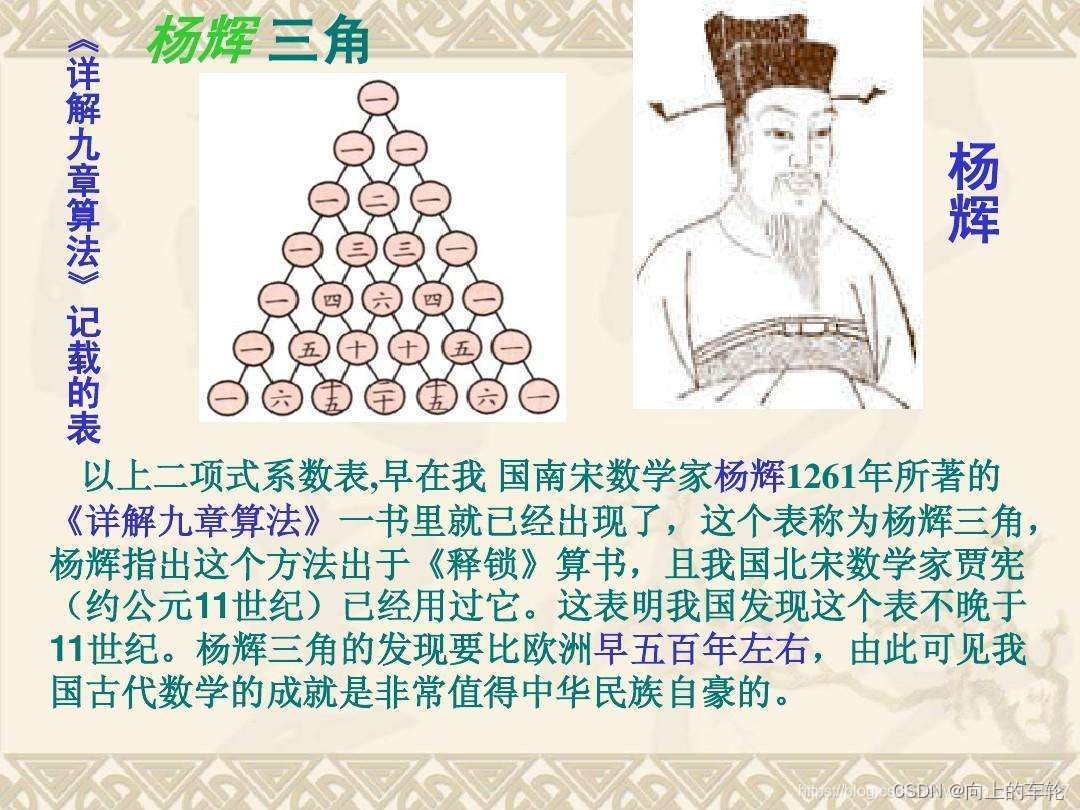
杨辉三角是一个著名的数学图形，它展示了二项式系数的排列方式。

杨辉三角是一种将二项式系数以三角形阵列排列的数学图形，具有丰富的历史和数学意义。

杨辉三角的历史起源可以追溯到中国南宋时期，由数学家杨辉在其1261年的著作《详解九章算法》中提出。它在欧洲被称为帕斯卡三角，因为法国数学家布莱士·帕斯卡在1654年独立发现了同样的规律，比杨辉晚了393年。这个三角形不仅在数学史上有着重要地位，而且其简洁的形式和内在的数学规律使其成为教育和研究的重要工具。

杨辉三角的基本性质包括：

边界数为1：每行的第一个和最后一个数字总是1。
对称性：它是一个对称的三角形，从中心线可以看出二项式系数的对称性。
线性规律：每行的数字等于它正上方两数字之和。

此外，杨辉三角与以下数学概念有紧密联系：

二项式定理：杨辉三角的每一行对应于二项式的展开系数，即(a+b)^n的各项系数。
组合数学：杨辉三角中的每个数字也可以被理解为组合数C(n, k)，表示从n个不同元素中选出k个元素的组合方式的数量。
数论：在杨辉三角中，还隐藏着许多关于质数和它们的倍数的有趣模式和规律。

总的来说，杨辉三角不仅是中学数学课程的一部分，也被编程专家用于算法设计和问题求解。它的简单外形和复杂的内在规律使得杨辉三角继续吸引着从中学生到专业数学家的广泛关注。

二、用Rust打印杨辉三角

在Rust语言中，我们可以使用嵌套循环和向量来实现打印一个杨辉三角的功能。

是什么：杨辉三角是一个以二项式系数为基础的三角形排列，每一行的数字都是上一行相邻两个数字之和。例如，第一行为1，第二行为1 1，第三行为1 2 1，以此类推。
为什么：杨辉三角在数学中有着广泛的应用，例如计算二项式展开、组合数等。通过编程实现杨辉三角的打印，可以帮助我们更好地理解其规律和性质。
怎么办：在Rust中，我们可以使用以下步骤实现打印一个杨辉三角的功能：

a. 首先，我们需要创建一个向量来存储每一行的数据。
b. 然后，使用嵌套循环来计算每一行的数据。外层循环控制行数，内层循环控制每一行的元素。
c. 在内层循环中，我们需要判断当前元素是否为第一个或最后一个元素，如果是，则将其设置为1；否则，将其设置为上一行相邻两个元素之和。
d. 最后，将每一行的数据打印出来。

fn main() {
    let n = 10; // 设置杨辉三角的行数
    let mut triangle = vec![vec![1; n]; n]; // 初始化一个n行的向量，每行元素都为1

    for i in 1..n {
        for j in 1..i {
            triangle[i][j] = triangle[i - 1][j - 1] + triangle[i - 1][j]; // 计算当前元素
        }
    }

    for row in &triangle {
        for num in row {
            print!("{:<5}", num); // 打印每一行，每个元素占5个字符宽度
        }
        println!();
    }
}

1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 2 1 1 1 1 1 1 1 1
1 3 3 1 1 1 1 1 1 1
1 4 6 4 1 1 1 1 1 1
1 5 10 10 5 1 1 1 1 1
1 6 15 20 15 6 1 1 1 1
1 7 21 35 35 21 7 1 1 1
1 8 28 56 70 56 28 8 1 1
1 9 36 84 126 126 84 36 9 1

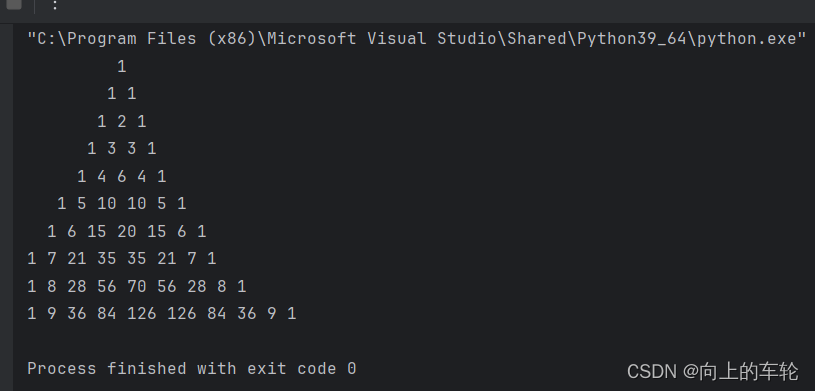
三、用Python打印杨辉三角

def generate_pascals_triangle(num_rows):
    triangle = []

    for row in range(num_rows):
        new_row = [1] * (row + 1)
        for i in range(1, row):
            new_row[i] = triangle[row - 1][i - 1] + triangle[row - 1][i]
        triangle.append(new_row)

    return triangle

def print_pascals_triangle(triangle):
    for row in triangle:
        print(" ".join(str(num) for num in row).center(len(triangle[-1]) * 2))

num_rows = 10
triangle = generate_pascals_triangle(num_rows)
print_pascals_triangle(triangle)