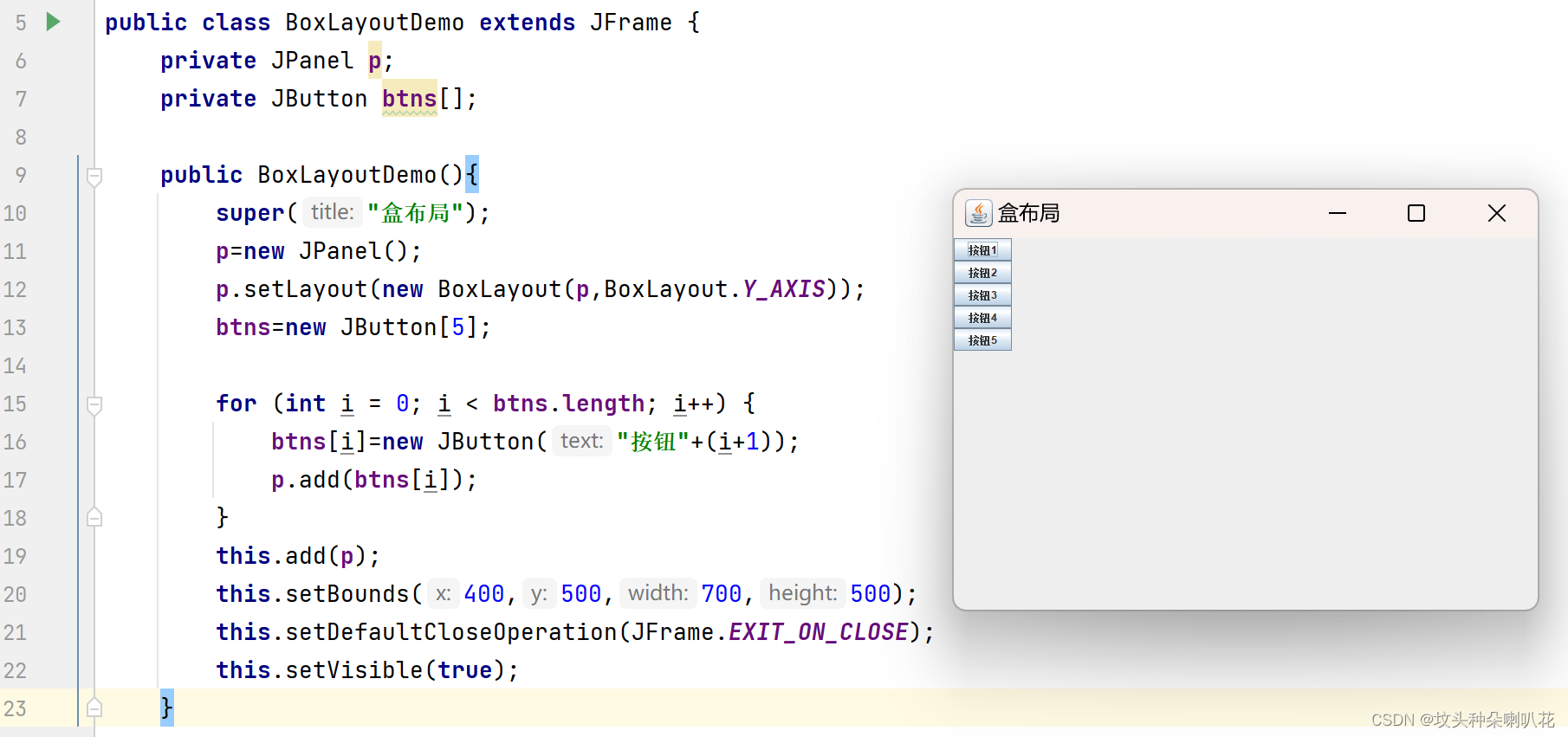
1 下载
Node.js — Run JavaScript Everywhere
LTS -- long-term support,长期维护版本
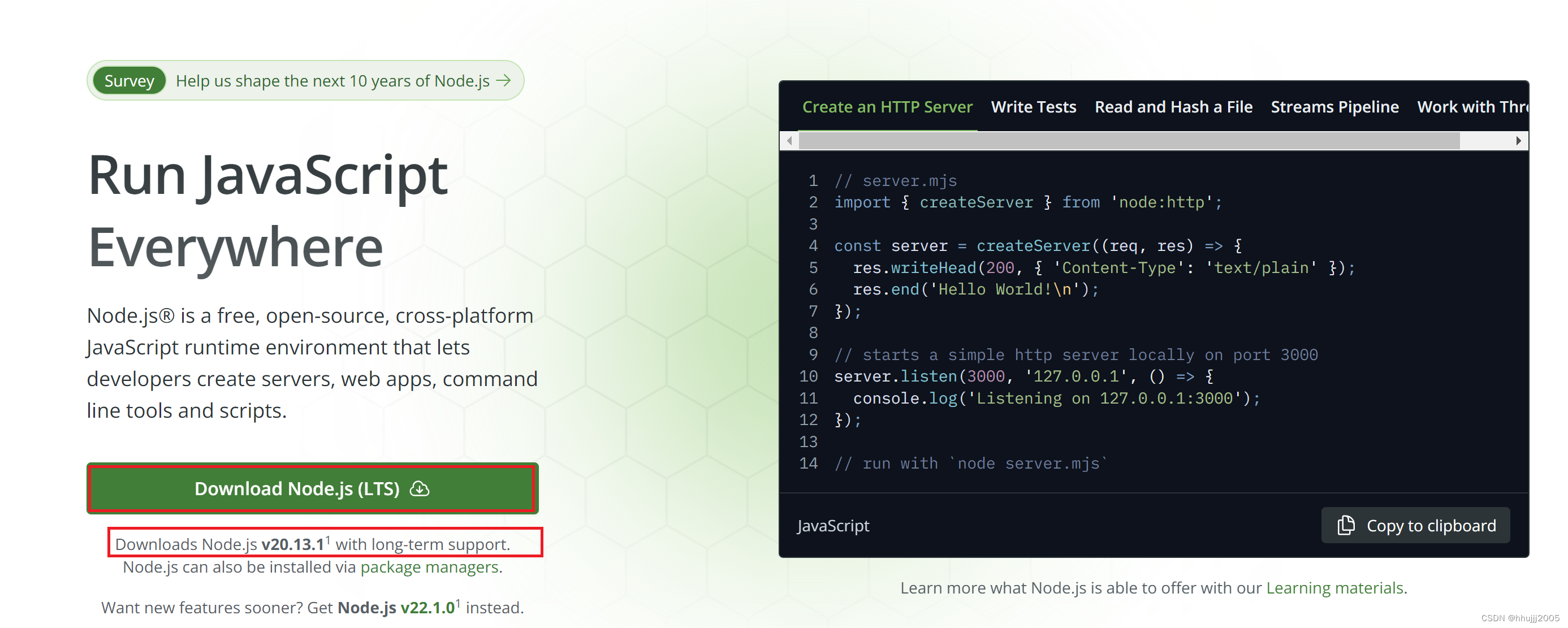
如果要下载其他版本在download里选择下载

2 安装
一路点击next,默认安装路径C:\Program Files\nodejs
3 环境变量配置
1)Path环境变量增加nodejs安装路径

2)验证是否安装成功
打开命令提示符,输入node -v和npm -v

4 配置组件和缓存目录
1)新建目录

2)设置参数prefix和cache
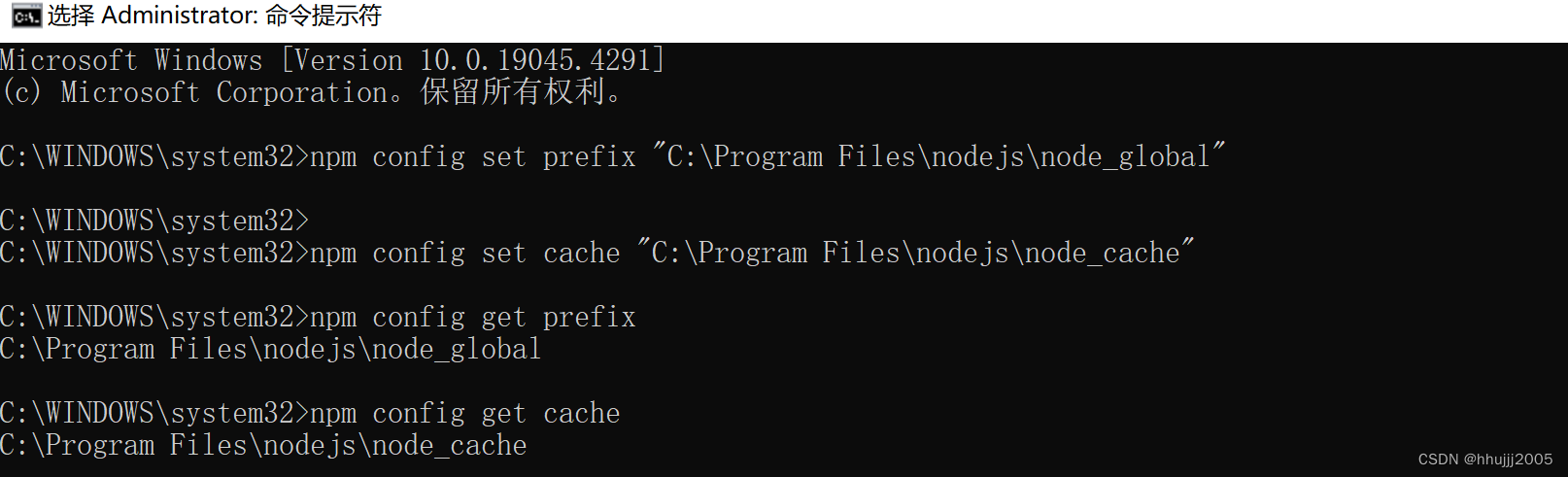
5 设置淘宝镜像
npm(Node Package Manager)是Node.js下的主流套件管理程式
npm和cnpm:国外的npm源在国内访问速度较慢,所以cnpm镜像源可以提供更快的下载速度
// 查询npm镜像
npm config get registry
// 设置淘宝镜像
// 旧
npm config set registry https://registry.npm.taobao.org/
// 新
npm config set registry https://registry.npmmirror.com
// 更换回原来的npm镜像
npm config set registry https://registry.npmjs.org
// 安装cnpm
npm install -g cnpm
// 查看是否安装成功
cnpm -vcnpm安装成功

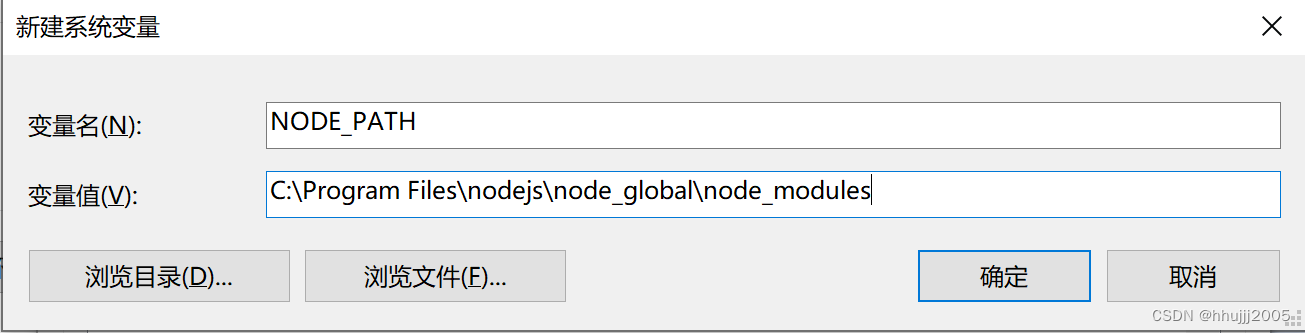
6 设置NODE_PATH环境变量(暂时可以不设置)
1)nodejs中的全局安装和局部安装:实习打怪之路:nodejs中的npm全局安装和局部安装的意思,npm中的全局安装和局部安装的区别_npm全局安装和局部安装有什么分别-CSDN博客
2)NODE_PATH
NODE_PATH是nodejs中用来寻找模块所提供的路径注册环境变量,并且用;分割多个不同的目录。
加载时机
NODE_PATH中的路径被遍历是发生在从项目的根位置递归搜寻 node_modules 目录,直到文件系统根目录的 node_modules,如果还没有查找到指定模块的话,就会去 NODE_PATH中注册的路径中查找。