【勘误】一个错误的快速排序实现

文章目录

- 问题一：不一致
- - 算法描述部分给出的分划实现
  - 完整程序部分给出的分划实现
- 问题二：不正确
- 问题三：把循环条件改为 `i <= j` 程序还是不正确
- 正确的实现
- 总结

从 $10$ 年前我开始学 C 语言时我就认为快速排序并不是个简单的算法。相比于归并排序，快速排序，具有非常多的容易出错的实现细节。稍有不慎就可能写出时间复杂度不对甚至不具有正确性的算法。

最近读到一本名为《C++面向对象程序设计》的书，机械工业出版社出版，ISBN 为 9787111656708，版次为 $2020$ 年 $6$ 月第 $1$ 版第 $1$ 次印刷。经过细致地分析，我发现该书第 17.2.1 节给出的快速排序算法有明显错误，在此发表勘误。

追根溯源，我在该书英文版《C++ Programming: An Object-Oriented Approach》中也发现了同样的问题，英文版 ISBN 为 9780073523385。

问题一：不一致

该书在算法描述中给出的分划代码实现与完整程序实现中给出的实现不一致，这种不一致导致完整程序中给出的代码明显不能应对被排序数组中存在重复元素的情况。

算法描述部分给出的分划实现

分划实现

完整程序部分给出的分划实现

在这里插入图片描述

我们可以看到，在完整程序代码第 $59$ 行以及第 $66$ 行后，相比于算法描述部分的代码缺少了语句 j-- 以及 i++。倘若调用函数 partition 时，arr[i] 与 arr[j] 在初始时具有相同的值，则程序将陷入死循环。

有人可能会质疑，该算法在数组中元素个数互不相同时是否能够正确地得到排序结果，从而猜想原作者只是想编写一个仅适用于不存在重复元素的数组排序的程序。但下文中我们可以证明，即使原始数组中不存在任何重复元素，我们同样可以构造出一个让该程序无法得出正确结果的反例。

问题二：不正确

即使我们按照算法描述中的部分修改了最终的完整程序，该程序仍然不具有正确性，即存在一个数组使得该程序无法正确地将该数组递增排序。下文中给出的代码出了输入输入的方式外，其余部分均与书中提供的算法一致。

#include <iostream>
using namespace std;

void swap(int& x, int& y);
void print(int arr[], int size);
int partition(int arr[], int beg, int end);
void quickSort(int arr[], int beg, int end);

int main() { // 为了方便测试，我们对原始程序稍加修改，让其从标准输入读入数组 arr 的内容
    int n; cin >> n;                 // 输入待排序数组的元素总数
    int* arr = new int[n];
    for(int i = 0; i < n; i += 1) {  // 输入待排序数组
        cin >> arr[i];
    }

    cout << "Original array:" << endl;
    print(arr, n);
    quickSort(arr, 0, n-1);
    cout << "Sorted array:" << endl;
    print(arr, n);

    delete[] arr;
    return 0;
}

void swap(int& x, int& y) {
    int temp = x;
    x = y;
    y = temp;
}

void print(int array[], int size) {
    for(int i = 0; i < size; i ++) {
        cout << array[i] << " ";
    }
    cout << endl;
}

int partition(int arr[], int i, int j) { // 这个分划写得不对
    int p = i;
    while(i < j) {
        while(arr[j] > arr[p]) {
            j --;
        }
        swap(arr[j], arr[p]);
        p = j;
        j --; // 这里我们修正了 “问题一” 中指出的问题
        while(arr[i] < arr[p]) {
            i ++;
        }
        swap(arr[i], arr[p]);
        p = i;
        i ++;
    }
    return p;
}

void quickSort(int arr[], int beg, int end) {
    if(beg >= end || beg < 0) {
        return;
    }
    int pivot = partition(arr, beg, end);
    quickSort(arr, beg, pivot - 1);
    quickSort(arr, pivot+1, end);
}

在修正了 “问题一” 中指出的问题后，我们不难发现，其实这个算法还是不正确。比如我们可以让其排序 4, 5, 1, 3 四个数。程序给出了如下输出：
在这里插入图片描述
程序给出的排序结果为 3, 4, 1, 5，而正确的排序后结果应该为 1, 3, 4, 5。而这个问题是如何产生的呢？

观察分划函数第一次执行的过程：

int partition(int arr[], int i, int j) { // 这个分划写得不对
    int p = i;
    while(i < j) {
        while(arr[j] > arr[p]) {
            j --;
        }
        swap(arr[j], arr[p]);
        p = j;
        j --; // 检查点 1
        while(arr[i] < arr[p]) {
            i ++;
        }
        swap(arr[i], arr[p]);
        p = i;
        i ++; // 检查点 2
    }
    return p; // 检查点 3
}

我们核心关注上述程序执行 “检查点1”，“检查点2”，“检查点3”，三处语句后数组中元素的值以及 i, j, p 三个变量的取值情况。

时刻	`arr`	`i`	`j`	`p`
初始	`{4, 5, 1, 3}`	`0`	`3`	`0`
检查点 1	`{3, 5, 1, 4}`	`0`	`2`	`3`
检查点 2	`{3, 4, 1, 5}`	`2`	`2`	`1`
此时 `i==j` 外层循环退出
检查点 3	`{3, 4, 1, 5}`	`2`	`2`	`1`

此时程序认定 $a rr [1] = 4$ 即当前轮主元已经被放置在了正确的位置上，而实际上由于 arr[2]=1 从来未被比较过，但此时 i==j 已经成立，所以程序认为主元归位。而这个错误源于一个错误的直觉：即，在算法执行的过程中 $i$ 以及 $i$ 左侧的所有位置一定小于等于主元， $j$ 以及 $j$ 右侧的元素一定大于等于主元。但实际上，由于检查点 1 处以及检查点 2 处添加的语句 j -- 和 i++ 的存在，使得每当进入循环 while(i < j) 时，程序其实仍未对 arr[i] 与 arr[j] 进行过任何比较。因此我们应断言：数组在下标闭区间 [i, j] 内的部分，实际上从未被比较过，因此 i < j 这一循环条件会导致分划程序提前终止。

问题三：把循环条件改为 `i <= j` 程序还是不正确

需要注意的是，如果仅仅是把循环条件改为 i <= j 程序仍然不正确。修改后的分划函数如下：

int partition(int arr[], int i, int j) { // 这个分划写得不对
    int p = i;
    while(i <= j) { // 我们修改了分划的结束条件
        while(arr[j] > arr[p]) {
            j --;
        }
        swap(arr[j], arr[p]);
        p = j;
        j --; // 检查点 1
        while(arr[i] < arr[p]) {
            i ++;
        }
        swap(arr[i], arr[p]); // 错误来源这里
        p = i;
        i ++; // 检查点 2
    }
    return p; // 检查点 3
}

在此我们仍然可以给出反例，例如让 arr 取 {1, 2, 1}，程序可以得到如下的结果：
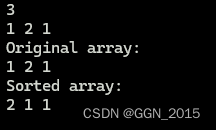
在这里插入图片描述
尽管 {2, 1, 1} 看起来是有序的，但我们希望读者记得，我们的排序算法是要将原数组递增排序而不是要将原数组递减排序。因此这个结果也是错误的。而这个错误是由 swap(arr[i], arr[p]); 这条语句导致的。在算法执行的过程中我们确实能够大致证明：

i 左侧的所有位置（不含 i）小于等于主元；（条件 1）
j 右侧的所有位置（不含 j）大于等于主元；
常见的快速排序一般要保证算法执行过程中上述两个条件总是成立的。
在分划执行过程中由于 swap 以及对 p 的赋值语句总是成对出现，所以 p 指向的位置的值总是与初始的主元值一致。

但是实际上当 i 与 j 十分接近时，在执行语句 swap(arr[i], arr[p]); 前 p 可能已经位于 i 的左侧。此时很可能导致将 i 左侧的一个值与 arr[i] 交换。而这修改了 i 左侧已经扫描过的内容，于是使得条件 1 出现了可能不成立的情况，算法的正确性也就难以保证了。

参照问题二中设置检查点的方式，我们可以追踪 arr, i, j, p 四个变量的值的变化：

时刻	`arr`	`i`	`j`	`p`
初始	`{1, 2, 1}`	`0`	`2`	`0`
检查点 1	`{1, 2, 1}`	`0`	`1`	`2`
检查点 2	`{1, 2, 1}`	`1`	`1`	`0`
检查点 1	`{1, 2, 1}`	`1`	`-1`	`0`
检查点 2 (*)	`{2, 1, 1}`	`1`	`-1`	`1`
此时 `i==j` 外层循环退出
检查点 3	`{2, 1, 1}`	`1`	`-1`	`1`

我们可以看到错误的交换出现于 (*) 处，此时 i 左侧的内容本来是符合条件 1 的，但是由于我们不知道 p 也在 i 的左侧，所以错误地将 i 处本身不符合条件 1 的值交换到了 i 的左侧。

正确的实现

修改了上述三个问题后，我们给出一个可能正确的快速排序算法。初始时我们令 i=beg+1 而不是令 i=beg 是为了在证明过程中更方便地构造递归的子结构。因为我们可以看到，每当我们进入 while(i < j) 这一循环时，p 总是等于 i-1。而原书中给出的代码的正确性是更难以证明的，因为原书中第一次进入外层循环体时 p 等于 i 而其他时刻 p 等于 i-1，这为数学证明带来了不必要的 Trivial Exception。

#include <algorithm>
#include <cstdio>
using namespace std;

int rand(int l, int r) {
    return rand() % (r - l + 1) + l;
}

int findPos(int arr[], int beg, int end) {
    int i = beg + 1, j = end; // 这里的修改有利于正确性证明
    int p = beg;
    swap(arr[beg], arr[rand(beg, end)]); // 解决 TLE 问题
    while(i < j) {
        while(arr[p] < arr[j]) j --;
        swap(arr[p], arr[j]);
        p = j;
        j --;
        while(arr[p] > arr[i]) i ++;
        if(p > i) { // 这里要保护 i 左侧的值的正确性
            swap(arr[p], arr[i]);
            p = i;
            i ++;
        }
    }
    if(i == j && p == i - 1) { // 这里要放置 i 和 j 恰好相遇导致存在未被考虑的区间
        if(arr[i] < arr[p]) {
            swap(arr[i], arr[p]);
            p = i;
        }
    }
    return p;
}

void quickSort(int arr[], int beg, int end) {
    if(beg >= end) {
        return;
    }
    int pos = findPos(arr, beg, end);
    quickSort(arr, beg, pos-1);
    quickSort(arr, pos+1, end);
}

const int maxn = 1e6 + 7;
int arr[maxn];
int main() {
    int n; scanf("%d", &n);
    for(int i = 1; i <= n; i += 1) {
        scanf("%d", &arr[i]);
    }
    quickSort(arr, 1, n);
    for(int i = 1; i <= n; i += 1) {
        printf(" %d" + (i == 1), arr[i]);
    }
    putchar('\n');
    return 0;
}

总结

无论是对于初学者来说，还是对于经验丰富的程序员来说，写出一个正确的快速排序来总是很难的。当不得不自己手写排序时，我强烈建议选择归并排序而不是快速排序，因为快速排序的各种写法，其实都有莫名其妙的边界条件需要验证。当我们不关注排序的实现细节而只是要使用排序时，能用编程语言的标准库中提供的 sort 函数或者 stable_sort 函数，就不要自行手写，这无疑是一句中肯的忠告。

教编程的这些年里我见过形形色色的快速排序实现，而鲜有人关注这些实现的正确性证明（有的证明也是错的），其中很多实现都有奇奇怪怪的问题。例如有的实现时间复杂度不对，能够被容易地卡成 $O(n^2)$ 的时间复杂度（即使随机选择主元）。有的实现在数组中存在重复元素时会出错，有的实现要求在数组末尾添加一个 inf 才能保证算法正确退出…

不要因为快速排序写起来很短就可以不认真地对待它。编程这件事，往往失之毫厘谬以千里。