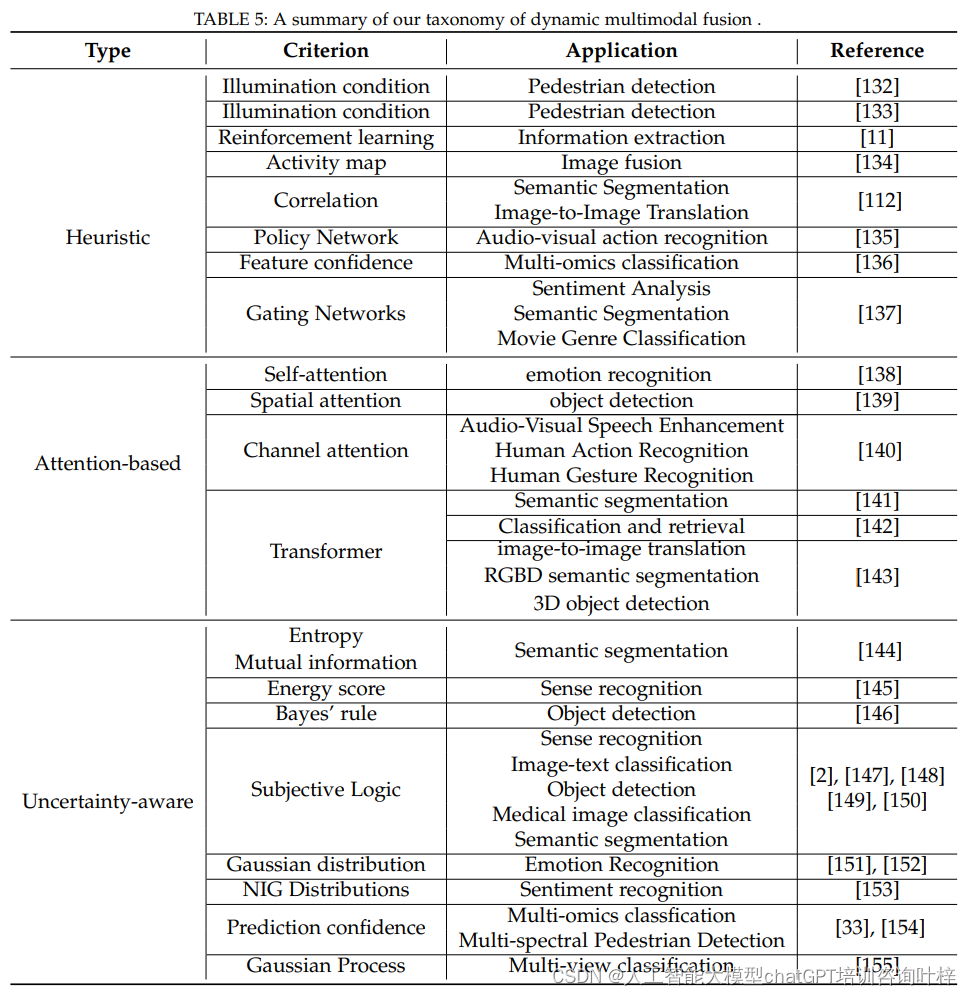
手写Minist识别是一个非常经典的问题，其数据集共有70000张28*28像素的图片，其中60000张作为训练集，剩下的10000张作为测试集，每一张图片都表示了一个手写数字，经过了灰度处理。
本文延续前面文章提到的多层感知机，在这里完成更复杂的任务，这个也可以作为分类任务的代表。

1.导入数据

首先导入模型，我个人的习惯是在同名目录下新建static文件夹存放一些数据，这里先建好static/data，然后就可以等待下载数据了，文件夹关系如下：

在这里，尽管导入的时候已经是batch的形式了，为了后面方便起见，我还将训练集和测试集分别按照numpy的格式组装为一个个batch，然后将标注进行独热编码，具体的代码可以看后面的完整代码。

2.训练模型

​
训练模型是最复杂的部分，这里涉及到前向传播和反向传播，这部分在我前面的博客中提到过，不再赘述，不同的是多出了在每个隐藏层和输出层进行了批量规范化（Batch Normalization），也就是BN层，在这里简单展开介绍一下。
（感觉我自己写的部分可能只能我自己看得懂了…建议可以顺着我推荐的博客或者其他人的好好了解一下，我写的比较简单）

建议先看这两篇：
1. 知乎，这一篇主要是介绍一些优点

2. 知乎，这一篇的推导非常详细
​先考虑在训练时的情况，给出表达式，假设输入为$x$，输出为$o$，维度均为$n\times 1$，那么在$BN$层中经过了如下变换：
$$\begin{gathered} \mu =\frac{1}{m}\sum _{i=1}^n{x}_i \\ {\sigma }^2=\frac{1}{m}\sum _{i=1}^n(x_i-\mu {)}^2 \\ \hat{x}=\frac{x-\mu }{\sqrt{{\sigma }^2+ϵ}} \\ o=\gamma \hat{x}+\beta \end{gathered}$$
$\mu ,\sigma$分别是均值和方差，下面的$\hat{x}$也就是经过标准化的$x$，加入最后的$\gamma ,\beta$是缩放和平移的系数，通过学习得到。

得到了表达式，那么下面讨论参数更新的问题，也就是反向传播，不考虑$o$之后到损失函数的，因为之后的都可以用$\frac{\partial L}{\partial o_i}$给出。

先给出$\gamma$和$\beta$的：
$$\begin{gathered} \frac{\partial o_i}{\partial \gamma }={\hat{x}}_i \\ \frac{\partial o_i}{\partial \beta }=1 \end{gathered}$$
由于输入是$x$，这个和前面的层直接关联，因此输出$o$和$x$的关系也很重要，计算过程如下：
$$\frac{\partial o_i}{\partial x_i}=\frac{\partial \mu }{\partial x_i}\frac{\partial o_i}{\partial \mu }+\frac{\partial {\sigma }^2}{\partial x_i}\frac{\partial o_i}{\partial {\sigma }^2}+\frac{\partial {\hat{x}}_i}{\partial x_i}\frac{\partial o_i}{\partial {\hat{x}}_i}$$
这里要注意的是有三个关于$x$的变量的链式求导，$x$在关于$x,{\sigma }^2,\hat{x}$的表达式中都出现了，因此链式求导都要加上，这在具体计算$\frac{\partial o_i}{\partial \mu },\frac{\partial {\hat{x}}_i}{\partial x_i}$等都要注意，下面写一个$\frac{\partial o_i}{\partial \mu }$的：
$$\frac{\partial o_i}{\partial \mu }=\frac{\partial {\hat{x}}_i}{\partial \mu }\frac{\partial o_i}{\partial {\hat{x}}_i}+\frac{\partial {\sigma }^2}{\partial \mu }\frac{\partial o_i}{\partial {\sigma }^2}$$
这里之所以还有关于${\sigma }^2$是因为$\sigma$的表达式直接出现了$\mu$。

下面是一些过程，实际的使用是和损失函数$L$的关系，下面框出的是看不懂的，去问了，不知道作者会不会回复。

具体的过程这里不写了，就直接抄博客的最简表达式了(因为太抽象了…)

他的表达式如下：

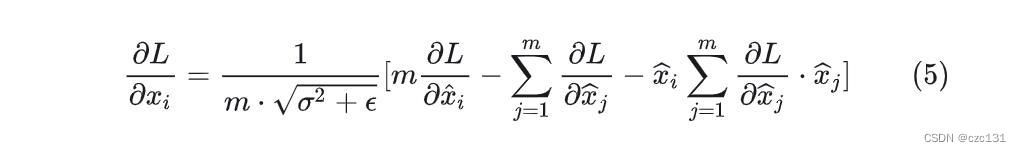
在这样的情况下，原本更新$w$的都要变化。假设经过线性累加后为$N$，激活后为$O$，那么原本$L$关于$w$的链式传播为：
$$\frac{\partial L}{\partial w}=\frac{\partial N}{\partial w}\frac{\partial O}{\partial N}\frac{\partial L}{\partial O}$$
现在在$O$和$N$之间多出了$BN$层，那么链式传播就要发生变化，假设$BN$层为$B$，先经过$BN$层然后经过激活函数（一般对于ReLU是这个顺序），那么有下式：
$$\frac{\partial L}{\partial w}=\frac{\partial N}{\partial w}\frac{\partial B}{\partial N}\frac{\partial O}{\partial B}\frac{\partial L}{\partial O}$$
先看$\frac{\partial O}{\partial B}\frac{\partial L}{\partial O}$，对于反向传播来说，输入到底是$B$（现在）还是$N$（原来）都不重要，因为这个式子的计算不涉及这个值，只和输出$O$有关，因此可以等同于原来的损失$\delta$：
$$\frac{\partial O}{\partial B}\frac{\partial L}{\partial O}={\delta }_{Layer,j}=\{\begin{array}{c}g(O_{Layer,j}){\sum }_{k=1}^K{w}_{jk}{\delta }_{Layer+1,k},Layer不为输出\\ g(O_{Layer,j})(O_{Layer,j}-labe{l}_k),Layer为输出\end{array}$$
这里的$g(x)$表示激活函数的导数。

写到这一步，其实上面最终表达式的$\frac{\partial L}{\partial x_i}$已经可以表示了，他的$x_i$其实就表示这里的$N$，也就是$BN$层的输入，写出表达式的等效：（为了和上面一致，把$x_i$写为$x$）
$$\frac{\partial L}{\partial x}=\frac{\partial B}{\partial N}\frac{\partial L}{\partial B}=\frac{\partial B}{\partial N}\delta =f(\frac{\partial B}{\partial \hat{x}}\delta )=f(\gamma \delta )$$
这个$f(x)$就是上面的求解公式，将$\gamma \delta$替换掉$\frac{\partial L}{\partial \hat{x}}$即可。

其他的其实跟前面提到的神经网络没什么区别了，在代码中我把隐藏层的偏置都去掉了，因为有的博客提到了BN层的偏置就不需要隐藏层的偏置了。（正好这个偏置又很难写）

在真正预测的时候，这时候无法计算出批对应的均值和标准差，这里采用的是统计训练过程中的均值$\mu$和方差${\sigma }^2$，用于预测时进行规范化。

3.模型运行

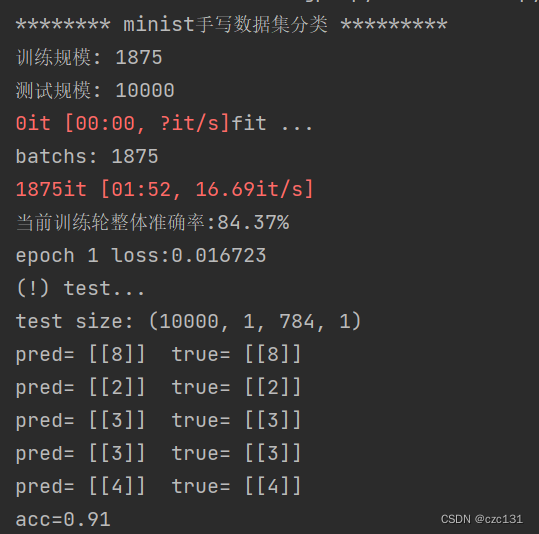
模型运行无论之后的结果：（显示出来的都是预测的前面五个的结果）

因为没有很多优化，代码运行的效率并不算好，只能说勉强能跑（在 batch_size = 32 的情况下大约两分钟训练完一轮），在训练完第一轮的时候在测试集的准确率就已经达到大约90%了，后面几轮的提升不大。
没试过其他batch_size或者调参之类的，能跑应该就是没问题的吧？

4.完整代码

下面贴出完整代码，写的有冗余，写法也很抽象，仅供学习参考哈（很多推导我在前面的博客都提到过，这一篇就没有多说了）

# 手写Minist数据集分类
import numpy as np
import torch
import torchvision
from matplotlib import pyplot as plt
from numpy import log
from numpy.random import uniform
from sklearn.metrics import accuracy_score
from tqdm import tqdm

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


def load_data(if_reload=False):
    batch_size_train = 32
    batch_size_test = 1
    random_seed = 1
    torch.manual_seed(random_seed)
    train_loader = torch.utils.data.DataLoader(
        torchvision.datasets.MNIST('./static/data/', train=True, download=True,
                                   transform=torchvision.transforms.Compose([
                                       torchvision.transforms.ToTensor(),
                                       torchvision.transforms.Normalize(
                                           (0.1307,), (0.3081,))
                                   ])),
        batch_size=batch_size_train, shuffle=True)
    test_loader = torch.utils.data.DataLoader(
        torchvision.datasets.MNIST('./static/data/', train=False, download=True,
                                   transform=torchvision.transforms.Compose([
                                       torchvision.transforms.ToTensor(),
                                       torchvision.transforms.Normalize(
                                           (0.1307,), (0.3081,))
                                   ])),
        batch_size=batch_size_test, shuffle=True)
    train_size = len(train_loader)
    test_size = len(test_loader)
    print('训练规模:', train_size)
    print('测试规模:', test_size)

    # 设置类别的数量
    num_classes = 10
    onehot = np.eye(num_classes)
    X_train = np.zeros((train_size, batch_size_train, 784, 1), dtype=np.float32)
    y_train = np.zeros((train_size, batch_size_train, 10, 1), dtype=int)  # 要独热编码
    X_test = np.zeros((test_size, batch_size_test, 784, 1), dtype=np.float32)
    y_test = np.zeros((test_size, batch_size_test, 1), dtype=int)  # 不需要进行独热编码
    # 训练
    for batch_idx, (data, target) in enumerate(train_loader):
        if data.shape[0] < batch_size_train:
            break
        X_train[batch_idx] = np.array(data).reshape(batch_size_train, -1, 1)  # 展平放入
        y_train[batch_idx] = onehot[target].reshape(batch_size_train, -1, 1)  # 将整数转为一个10位的one hot编码

    # 测试
    for batch_idx, (data, target) in enumerate(test_loader):
        if data.shape[0] < batch_size_test:
            break
        X_test[batch_idx] = np.array(data).reshape(batch_size_test, -1, 1)  # 展平放入
        y_test[batch_idx] = np.array(target).reshape(batch_size_test, -1, 1)
    return X_train, y_train, X_test, y_test


class MyNet():
    def __init__(self):
        self.eps = 0.00001  # 极小值
        self.new_rate = 0.1  # 均值新值所占的比例
        self.alpha_BN = 0.005

    # sigmoid
    def sigmoid(self, x):
        return 1 / (1 + np.exp(-x)) + self.eps  # 加上一个极小值

    # rule
    def rule(self, x):
        x[np.where(x < 0)] = 0
        return x

    # 损失函数
    def loss_func(self, output, label):  # 输入是batch*列向量
        out = log(output + self.eps)  # 加上一个极小值
        loss = -label.transpose(0, 2, 1) @ out
        return np.sum(loss.flatten())  # 总的损失(batch个)

    def softmax(self, out):  # 输入格式(batch,row,1),应该算出每个batch的最大值,然后减掉
        x = out.copy()
        res = np.zeros_like(x, dtype=np.float32)
        for i in range(x.shape[0]):
            x[i] -= max(x[i])
            expx = np.exp(x[i])
            sexpx = np.sum(expx)
            res[i] = expx / sexpx
        return res

    # batch norm
    def train_normlize(self, x, gamma, beta):  # 输入 (batch,rows,1)
        mmu = np.mean(x, axis=0)
        var = np.mean((x - mmu) ** 2, axis=0)  # rows,1
        ivar = 1 / np.sqrt(var + self.eps)  # rows,1
        x_hat = (x - mmu) * ivar  # [(batch,rows,1)-(rows,1)]/rows,1->batch,rows,1
        out = gamma * x_hat + beta
        return out, ivar, mmu, var, x_hat  # 后面mmu和var是为了累计总均值和标准差,所以传回,x_hat在更新系数γ需要用到

    def normlize_eval(self, x):  # 输入 (batch,rows,1)
        return (x - self.running_mmu) / self.running_var

    def fit(self, X, Y, test_x=None, test_y=None, epochs=30, test_epoch=1 ,alpha=0.01, layers=2, layer_size=3, activation='sigmoid'):
        # layer,layer_size:中间的隐藏层层数和隐藏层的大小
        print('fit ...')
        self.acti_func = self.sigmoid
        if activation == "rule":
            self.acti_func = self.rule
        else:
            assert "unknown activation algorithm: %s" % (activation)
        batch_size, in_features = X[0].shape[0], X[0].shape[1]
        out_features = Y[0].shape[1]
        batchs = len(X)
        batch_size = X[0].shape[0]  # batch大小
        print('batchs:', batchs)
        samples = batch_size * batchs

        # 矩阵初始化(随机初始化)
        w_first = uniform(-1, 1, (in_features, layer_size))  # 每一行是一个输入神经元对所有下一层神经元的权值,+1是偏置的权值(有BN层不需要)
        w_last = uniform(-1, 1, (layer_size, out_features))  # 每一行是一个输入神经元对所有下一层神经元的权值
        self.w = None  # 防止后续报错
        if layer_size > 1:  # 刚好等于1就不需要了
            w = uniform(-1, 1, (layers - 1, layer_size, layer_size))  # 每一层都大小+1

        # 运行过程中的变量(注意有了BN层不需要偏置了)
        delta = np.zeros((batch_size, layers, layer_size, 1), dtype=float)  # 前面每一层都要+1
        delta_last = np.zeros((batch_size, out_features, 1), dtype=float)  # 每一列是一层的δ
        out_last = np.ones((batch_size, out_features, 1), dtype=float)  # 每一列是一层的output
        out = np.ones((batch_size, layers, layer_size, 1), dtype=float)
        out_softmax = np.ones((batch_size, out_features, 1), dtype=float)  # 经过softmax得到的结果
        norm_gamma = np.ones((layers, layer_size, 1), dtype=float)
        norm_gamma_last = np.ones((out_features, 1), dtype=float)  # BN的γ
        norm_beta = np.zeros((layers, layer_size, 1), dtype=float)
        norm_beta_last = np.zeros((out_features, 1), dtype=float)  # BN的β
        ivar = np.zeros((layers, layer_size, 1), dtype=float)  # 1/sqrt(σ^2+eps)
        ivar_last = np.zeros((layers, out_features, 1), dtype=float)  # 1/sqrt(σ^2+eps)
        x_hat = np.zeros((batch_size, layers, layer_size, 1), dtype=float)
        x_hat_last = np.zeros((batch_size, out_features, 1), dtype=float)  # 每一列是一层的output
        # 下面是运行过程中需要统计的均值和标准差
        running_mmu = np.zeros((layers, layer_size, 1), dtype=float)
        running_mmu_last = np.zeros((out_features, 1), dtype=float)
        running_var = np.zeros((layers, layer_size, 1), dtype=float)
        running_var_last = np.zeros((out_features, 1), dtype=float)

        # 开始迭代
        loss_list = []
        for epoch in range(1, 1 + epochs):
            loss = 0
            cnt = 0
            pbar = tqdm(zip(X, Y))
            for idx, (x, y) in enumerate(pbar):
                # 前向传播
                # 输入->...layers->layer_-1->softmax->argmax()
                for layer in range(layers + 2):
                    # 先标准化再激活
                    if layer == 0:  # 第一层
                        xx = (w_first.T @ x)
                        out[:, layer, :], tmp, mmu, var, x_hat_ = self.train_normlize(
                            x=xx, gamma=norm_gamma[layer], beta=norm_beta[layer])
                        out[:, layer, :] = self.acti_func(out[:, layer, :])
                        x_hat[:, layer, :] = x_hat_
                        ivar[layer] = tmp
                        running_var[layer] = running_var[layer] * (1 - self.new_rate) + var * self.new_rate
                        running_mmu[layer] = running_mmu[layer] * (1 - self.new_rate) + mmu * self.new_rate
                    elif layer < layers:  # 不是最后一层
                        xx = (w[layer - 1].T @ out[:, layer - 1])
                        out[:, layer, :], tmp, mmu, var, x_hat_ = self.train_normlize(
                            x=xx, gamma=norm_gamma[layer], beta=norm_beta[layer])
                        out[:, layer, :] = self.acti_func(out[:, layer, :])
                        x_hat[:, layer, :] = x_hat_
                        ivar[layer] = tmp
                        running_var[layer] = running_var[layer] * (1 - self.new_rate) + var * self.new_rate
                        running_mmu[layer] = running_mmu[layer] * (1 - self.new_rate) + mmu * self.new_rate
                    elif layer == layers:  # 最后一层隐藏层到输出层
                        xx = w_last.T @ out[:, layer - 1]
                        out_last[:, :, :], tmp, mmu, var, x_hat_ = self.train_normlize(
                            x=xx, gamma=norm_gamma_last, beta=norm_beta_last)
                        out_last = self.acti_func(out_last)
                        ivar_last = tmp
                        x_hat_last[:, :, :] = x_hat_
                        running_var_last = running_var_last * (1 - self.new_rate) + var * self.new_rate
                        running_mmu_last = running_mmu_last * (1 - self.new_rate) + mmu * self.new_rate
                    else:
                        out_softmax = self.softmax(out_last)
                # 反向传播
                for layer in range(layers, -1, -1):  # layers,...,0
                    # 计算出每一层的损失
                    if layer == layers:  # 最后一层(输出层),这里直接用softmax层计算得到
                        # print('输出层')
                        if activation == 'sigmoid':
                            delta_last = out_last * (1 - out_last) * (out_softmax - y)
                            # 分类的导数实际和回归的一样,只不过多了个softmax过程,实际上还是一样的
                        elif activation == 'rule':
                            deriva = np.ones_like(out_last)
                            deriva[np.where(out_last < 0)] = 0
                            delta_last = deriva * (out_softmax - y)
                    elif layer == layers - 1:  # 隐藏层最后一层,连接输出层
                        # print('最后一层隐藏')
                        if activation == 'sigmoid':
                            delta[:, layer] = out[:, layer] * (1 - out[:, layer]) * (w_last @ delta_last)
                        elif activation == 'rule':
                            deriva = np.ones_like(out[:, layer])
                            deriva[np.where(out[:, layer] < 0)] = 0
                            delta[:, layer] = deriva * (w_last @ delta_last)
                    else:  # 最后一层
                        # print('隐藏')
                        if activation == 'sigmoid':
                            delta[:, layer] = out[:, layer] * (1 - out[:, layer]) * (
                                        w[layer] @ delta[:, layer + 1])  # 只有1-n会继续前向传播
                        elif activation == 'rule':
                            deriva = np.ones_like(out[:, layer])
                            deriva[np.where(out[:, layer] < 0)] = 0
                            delta[:, layer] = deriva * (w[layer] @ delta[:, layer + 1])
                # 更新系数(w和两个BN参数)
                for layer in range(layers + 1):
                    if layer == 0:  # 输入-隐藏
                        # print('输入-隐藏')
                        x_hat_ = x_hat[:, layer, :]  # x_hat少一行1(相比x)
                        det_gamma = np.sum(x_hat_ * delta[:, layer, :], axis=0)  # batch,rows-1,1 x rows-1,1
                        det_beta = np.sum(delta[layer, :], axis=0)  # beta其实跟b是一样的(本来有了BN层的偏置就不需要b了)
                        var_sqr = ivar[layer]  # rows,1
                        dxhat = norm_gamma[layer] * delta[:, layer, :]  # γ(do/dx_hat)*δ(dL/do)
                        dx = 1 / batch_size * var_sqr * (batch_size * dxhat - np.sum(dxhat, axis=0) -
                                                         x_hat_ * np.sum(dxhat * x_hat_, axis=0))
                        det_w = x @ dx.transpose([0, 2, 1])
                        det_w = np.mean(det_w, axis=0)
                        w_first = w_first - alpha * det_w  # O_{Layer-1,i}δ_{Layer,j}
                        norm_gamma[layer] -= self.alpha_BN * det_gamma
                        norm_beta[layer] -= self.alpha_BN * det_beta
                    elif layer < layers:  # 隐藏-隐藏
                        # print('隐藏-隐藏')
                        x_hat_ = x_hat[:, layer, :]  # x_hat少一行1(相比x)
                        det_gamma = np.sum(x_hat_ * delta[:, layer, :], axis=0)  # batch,rows-1,1 x rows-1,1
                        det_beta = np.sum(delta[layer, :], axis=0)  # beta其实跟b是一样的(本来有了BN层的偏置就不需要b了)
                        var_sqr = ivar[layer]  # rows,1
                        dxhat = norm_gamma[layer] * delta[:, layer, :]  # γ(do/dx_hat)*δ(dL/do)
                        dx = 1 / batch_size * var_sqr * (batch_size * dxhat - np.sum(dxhat, axis=0) -
                                                         x_hat_ * np.sum(dxhat * x_hat_, axis=0))
                        det_w = out[:, layer - 1] @ dx.transpose([0, 2, 1])
                        det_w = np.mean(det_w, axis=0)
                        w[layer - 1] = w[layer - 1] - alpha * det_w  # O_{Layer-1,i}δ_{Layer,j}
                        norm_gamma[layer] -= self.alpha_BN * det_gamma
                        norm_beta[layer] -= self.alpha_BN * det_beta
                    else:  # 隐藏-输出
                        # print('隐藏-输出')
                        x_hat_ = x_hat_last  # x_hat少一行1(相比x)
                        det_gamma = np.sum(x_hat_ * delta_last, axis=0)  # batch,rows-1,1 x rows-1,1
                        det_beta = np.sum(delta_last, axis=0)  # beta其实跟b是一样的(本来有了BN层的偏置就不需要b了)
                        var_sqr = ivar_last  # rows,1
                        dxhat = norm_gamma_last * delta_last  # γ(do/dx_hat)*δ(dL/do)
                        dx = 1 / batch_size * var_sqr * (batch_size * dxhat - np.sum(dxhat, axis=0) -
                                                         x_hat_ * np.sum(dxhat * x_hat_, axis=0))
                        det_w = out[:, layer - 1] @ dx.transpose([0, 2, 1])
                        det_w = np.mean(det_w, axis=0)
                        w_last = w_last - alpha * det_w  # O_{Layer-1,i}δ_{Layer,j}
                        norm_gamma_last -= self.alpha_BN * det_gamma
                        norm_beta_last -= self.alpha_BN * det_beta
                soft_fal = np.argmax(out_softmax, axis=1).flatten()
                y_fal = np.argmax(y, axis=1).flatten()
                cnt += np.where(soft_fal == y_fal)[0].size
                this_loss = self.loss_func(out_softmax, y)
                loss += this_loss / batch_size  # 平均每个样本误差
            print('当前训练轮整体准确率:%.2f%%' % (100 * cnt / (batch_size * len(X_train))))
            loss_list.append(loss / samples)  # 样本平均误差
            print('epoch %d loss:%.6f' % (epoch, loss / samples))

            running_var *= batch_size / (batch_size - 1)
            running_var_last *= batch_size / (batch_size - 1)  # 无偏估计预测
            # 保存参数
            self.w_first = w_first
            self.w_last = w_last
            self.w = w
            self.in_features = in_features
            self.out_features = out_features
            self.layers = layers
            self.layer_size = layer_size
            self.running_mmu = running_mmu
            self.running_mmu_last = running_mmu_last
            self.running_var = running_var
            self.running_var_last = running_var_last
            self.norm_gamma = norm_gamma
            self.norm_gamma_last = norm_gamma_last
            self.norm_beta = norm_beta
            self.norm_beta_last = norm_beta_last

            if epoch % test_epoch == 0:  # 一轮测试一次
                if test_x is None or test_y is None:
                    continue
                print('(!) test...')
                pred = self.predict(test_x)
                display_num = 5  # 显示的个数
                for i in range(display_num):
                    print('pred=', pred[i], ' true=', test_y[i])
                acc = accuracy_score(test_y.reshape(-1, 1), pred.reshape(-1, 1))
                print('acc=%.2f' % (acc))

        plt.plot(loss_list)
        plt.show()

    def predict(self, X):
        print('test size:',X.shape)
        w_first = self.w_first
        w_last = self.w_last
        w = self.w
        layers = self.layers
        out_features = self.out_features
        layer_size = self.layer_size
        batch_size = X.shape[1]  # 得到batch的大小
        running_mmu = self.running_mmu
        running_mmu_last = self.running_mmu_last
        running_var = self.running_var
        running_var_last = self.running_var_last
        norm_gamma = self.norm_gamma
        norm_gamma_last = self.norm_gamma_last
        norm_beta = self.norm_beta
        norm_beta_last = self.norm_beta_last

        out_last = np.ones((batch_size, out_features, 1), dtype=float)  # 每一列是一层的output
        out = np.ones((batch_size, layers, layer_size, 1), dtype=float)
        out_softmax = np.ones((batch_size, out_features, 1), dtype=float)  # 经过softmax得到的结果
        res = np.zeros((X.shape[0], batch_size, 1), dtype=int)
        for idx, x in enumerate(X):
            # 前向传播
            for layer in range(layers + 2):
                if layer == 0:  # 第一层
                    out[:, layer, :] = ((w_first.T @ x) - running_mmu[layer, :]) / np.sqrt(
                        running_var[layer, :] + self.eps)
                    out[:, layer, :] = norm_gamma[layer] * out[:, layer, :] + norm_beta[layer]
                    out[:, layer, :] = self.acti_func(out[:, layer, :])
                elif layer < layers:  # 不是最后一层
                    out[:, layer, :] = ((w[layer - 1].T @ out[:, layer - 1]) - running_mmu[layer, :]) / np.sqrt(
                        running_var[layer, :] + self.eps)
                    out[:, layer, :] = norm_gamma[layer] * out[:, layer, :] + norm_beta[layer]
                    out[:, layer, :] = self.acti_func(out[:, layer, :])
                elif layer == layers:  # 最后一层隐藏层到输出层
                    out_last = (w_last.T @ out[:, layer - 1] - running_mmu_last) / np.sqrt(running_var_last + self.eps)
                    out_last = norm_gamma_last * out_last + norm_beta_last
                    out_last = self.acti_func(out_last)
                else:
                    out_softmax = self.softmax(out_last)
            output = np.argmax(out_softmax, axis=1)
            res[idx] = output
        return res


if __name__ == '__main__':
    print('******** minist手写数据集分类 *********')
    X_train, y_train, X_test, y_test = load_data(if_reload=True)  # 获取标准化后的数据

    myNet = MyNet()
    myNet.fit(X_train, y_train, test_x=X_test, test_y=y_test, epochs=5, test_epoch=1, alpha=0.01, layers=2, layer_size=200,
              activation='rule')

    print('训练完毕')
    print('test...')
    pred = myNet.predict(X_test)
    display_num = 5  # 显示的个数
    for i in range(display_num):
        print('pred=', pred[i], ' true=', y_test[i])
    acc = accuracy_score(y_test.reshape(-1, 1), pred.reshape(-1, 1))
    print('acc=%.2f' % (acc))

差不多就是这样了，有什么问题的话可以欢迎指出