xLSTM: Extended Long Short-Term Memory
公和众和号:EDPJ(进 Q 交流群:922230617 或加 VX:CV_EDPJ 进 V 交流群)

目录
0. 摘要
1. 简介
2. 扩展的 LSTM
2.1 LSTM 回顾
2.2 sLSTM
2.3 mLSTM
2.4 xLSTM 架构
2.5 内存和速度考虑
4. 实验
5. 限制
6. 结论
0. 摘要
在 1990s,恒定误差旋转门(constant error carousel)和门控(gating)被引入作为长短期记忆(Long Short-Term Memory,LSTM)的核心思想。从那时起,LSTM 经受住了时间的考验,并为许多深度学习成功故事做出了贡献,特别是构成了第一个大型语言模型(LLMs)。然而,随着 Transformer 技术的出现,以可并行化的自注意力为核心,标志着一个新时代的开端,在规模上超越了 LSTM。我们现在提出一个简单的问题:当将 LSTM 的规模扩大到数十亿参数,并利用现代 LLM 的最新技术,同时减轻已知的 LSTM 限制时,我们能在语言建模方面取得多远?首先,我们引入具有适当归一化和稳定化技术的指数门控(exponential gating)。其次,我们修改 LSTM 的内存结构,获得:(i)带有标量内存、标量更新和新的内存混合的 sLSTM,(ii)完全可并行化的 mLSTM,具有矩阵内存和协方差更新规则。将这些 LSTM 扩展集成到残差块骨干中,得到了 xLSTM 块,然后将它们残差叠加到 xLSTM 架构中。指数门控和修改后的内存结构提升了 xLSTM 的能力,使其在性能和规模方面与最先进的 Transformers 和状态空间模型(SSM)相比表现出色。
1. 简介
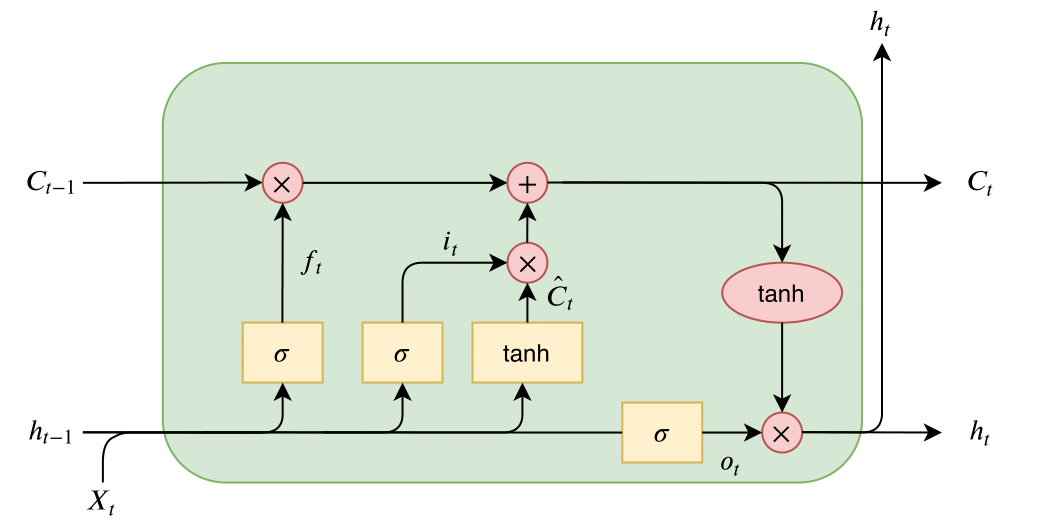
LSTM 的思想(Hochreiter, 1991; Hochreiter & Schmidhuber, 1997b,a),即恒定误差旋转门和门控,是为了克服 RNN(Hochreiter, 1991; Hochreiter et al., 2000)的梯度消失问题而引入的:
![]()
恒定误差旋转门是单元状态 c_(t−1)(绿色)通过单元输入 zt 的加法更新,并由 sigmoid 门(蓝色)调节。输入门 it 和遗忘门 ft 控制此更新,而输出门 ot 控制内存单元的输出,即隐藏状态 ht 。单元状态由 ψ 归一化或压缩,然后输出门给出隐藏状态。
尽管 LSTM 取得了巨大的成功,但仍存在三个主要限制:
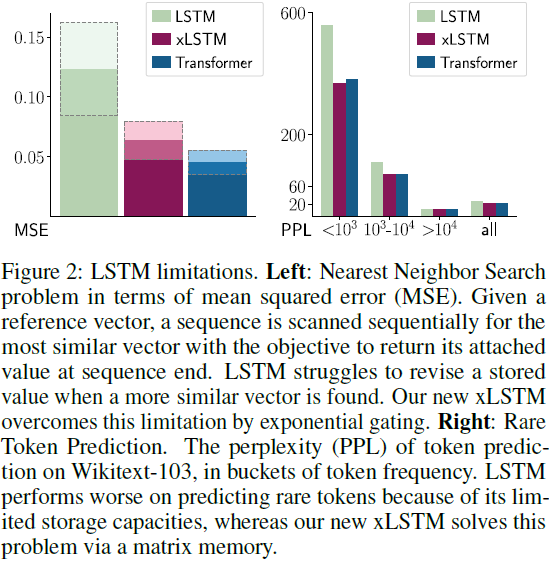
- 无法修订存储决策。我们通过最近邻搜索问题来说明这一限制(也见附录 B):给定一个参考向量,必须按顺序扫描序列,以找到最相似的向量,以便在序列末尾提供。图 2 的左侧面板显示了该任务的均方误差。当找到一个更相似的向量时,LSTM 在修订存储值时遇到困难,而我们的新 xLSTM 通过指数门控修复了这个限制。
- 有限的存储容量,即信息必须压缩到标量单元状态中。我们通过稀有标记预测(Rare Token Prediction)来说明这一限制。在图 2 的右侧面板中,给出了对 Wikite-103(Merity et al., 2017)上的标记预测的困惑度,针对不同标记频率的块(buckets)。由于其有限的存储容量,LSTM 在稀有标记上表现较差。我们的新 xLSTM 通过矩阵存储解决了这个问题。
- 由于记忆混合导致缺乏并行性,即从一个时间步到下一个时间步的隐藏状态之间的隐藏-隐藏连接,强制进行了顺序处理。
这些 LSTM 的限制为 Transformers(Vaswani et al., 2017)在语言建模中的出现铺平了道路。当克服这些限制并将 LSTM 扩展到当前大型语言模型的规模时,我们能够在语言建模中实现什么样的性能?
2. 扩展的 LSTM
2.1 LSTM 回顾
原始的 LSTM 思想(Hochreiter, 1991; Hochreiter & Schmidhuber, 1997b,a)引入了标量内存单元作为一个中心处理和存储单元,通过恒定误差旋转门(单元状态更新)避免了梯度消失(Hochreiter, 1991; Hochreiter et al., 2000)。内存单元包含三个门:输入门、输出门和遗忘门。遗忘门由 Gers 等人引入(2000年)。在时间步 t,LSTM 内存单元的更新规则为:

其中,
- 权重向量 w_z, w_i, w_f, 和 w_o 分别对应于输入 x_t 与单元输入、输入门、遗忘门以及输出门之间的输入权重向量。
- 权重 r_z, r_i, r_f, 和 r_o 对应于隐藏状态 h_{t-1} 与单元输入、输入门、遗忘门以及输出门之间的递归权重。
- b_z, b_i, b_f, 和 b_o 是相应的偏置项。
- φ 和 Ψ 是单元输入和隐藏状态激活函数(通常为双曲正切)。Ψ 用于归一化或压缩单元状态,否则将无界。
- 所有门的激活函数都是 sigmoid 函数,即 σ(x) = 1/(1 + exp(-x))。
在后续的公式中,多个内存单元被合并成一个向量,这允许使用递归权重矩阵来混合内存单元的单元输出(Greff et al., 2015),更多细节请参见附录 A.1。消融研究表明,内存单元的所有组件都至关重要(Greff et al., 2015)。

2.2 sLSTM
为了赋予 LSTM 修订存储决策的能力,我们引入了指数门控(红色)以及归一化和稳定化。特别地,输入门和遗忘门可以具有指数激活函数。对于归一化,我们引入一个归一化器(normalizer)状态,它将输入门与所有未来遗忘门的乘积相加。
sLSTM的前向传播过程是:

我们将原始的 LSTM 门控技术,即输入和/或隐藏依赖的门控以及偏置项,广播到新的架构中。指数激活函数可能导致产生大值而引起溢出。因此,我们使用额外的状态 m_t(Milakov & Gimelshein, 2018)来稳定门控:
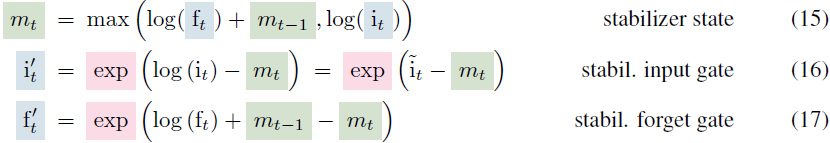
我们在附录 A.2 中展示,将 ft 替换为 f'_t,以及将 it 替换为 i'_t 在前向传播中既不会改变整个网络的输出,也不会改变损失对参数的导数。
新的内存混合。sLSTM 可以像原始的 LSTM 一样具有多个内存单元(见附录 A.2)。多个内存单元通过从隐藏状态向量 h 到内存单元输入 z 和门 i、f、o 的递归连接 rz、ri、rf、ro 实现内存混合。内存混合的新方面是指数门的影响。新的 sLSTM 可以在每个头部(head)内进行内存混合,但不能跨头部进行混合。引入头部对 sLSTM 的指数门以及内存混合建立了一种新的内存混合方式。
附录:基于 Greff 等人(2015)的标准 LSTM 内存单元更新规则,在时间步 t 将标量单元状态公式扩展为单元状态向量,类似地,sLSTM 也可以向量化为多个单元:
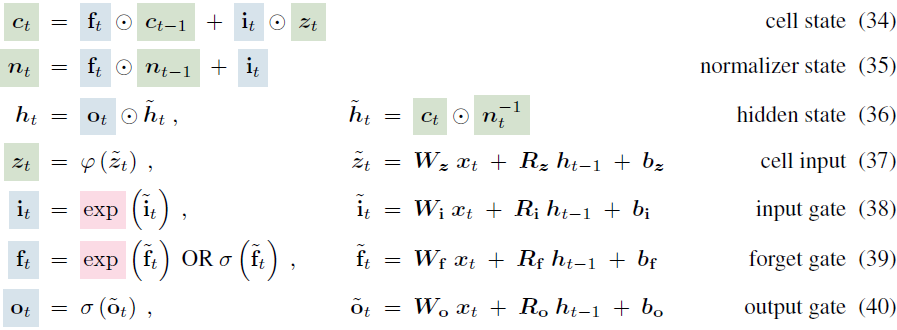
2.3 mLSTM
为了增强 LSTM 的存储容量,我们将 LSTM 内存单元从标量 c ∈ R 增加到矩阵 C ∈ R^(d×d)。因此,检索是通过矩阵乘法执行的。在时间 t,我们想要存储一对向量,即键 k_t ∈ R^d 和值 v_t ∈ R^d(我们使用 Transformer 术语)。稍后在时间 t + τ,值 v_t 应该由查询向量 q_(t+τ) ∈ R^d 检索。这是双向联想记忆(Bidirectional Associative Memories,BAMs)(Kohonen, 1972; Anderson, 1972; Nakano, 1972; Anderson et al., 1977)的设置。存储键-值对的协方差更新规则(Sejnowski, 1977; Dayan & Willshaw, 1991)是
![]()
我们假设在将输入投影到键和值之前进行层归一化,因此它们的平均值为零。协方差更新规则是最优的(Dayan & Willshaw, 1991),可实现检索的二进制向量的最大可分性,这等效于最大的信噪比。当将检索限制为成对交互并接受二次复杂度时,更高的可分性是可能的(Krotov & Hopfield, 2016, 2017; Ramsauer et al., 2021)。协方差更新规则等效于快速权重编程器(Schmidhuber, 1992; Schlag et al., 2021),后者已经配备了一个乘以 C_(t−1) 的恒定衰减率和一个乘以 v_t·k^T_t 的恒定学习率(Ba et al., 2016a)。在这个精神上,我们将协方差更新规则集成到 LSTM 框架中,其中遗忘门对应于衰减率,输入门对应于学习率,而输出门缩放检索到的向量。
对于这个矩阵内存,归一化器状态是键向量的加权和,其中每个键向量都由输入门和所有未来遗忘门加权。同样,归一化器状态记录门的强度。由于查询和归一化器状态之间的点积可能接近零,我们使用该点积的绝对值,并将其下限设为一个阈值(通常为 1.0),就像以前一样(Sun et al., 2023)。mLSTM 的前向传播过程是:

mLSTM 可以像原始的 LSTM 一样具有多个内存单元。对于 mLSTM,因为没有内存混合,多个头部和多个单元是等价的。为了稳定 mLSTM 的指数门,我们使用与 sLSTM 相同的稳定化技术,参见方程(15)。由于 mLSTM 没有内存混合,这种递归可以重新表述为并行版本。更多细节请参阅附录 A.3。
2.4 xLSTM 架构
xLSTM 块。xLSTM 块应该在高维空间中非线性地总结过去,以更好地区分不同的历史或上下文。分离历史是正确预测下一个序列元素(如下一个标记)的前提。我们诉诸于 Cover 定理(Cover, 1965),该定理指出在高维空间中,非线性嵌入的图样(patterns)更可能被线性分离,而不是在原始空间中。我们考虑两种残差块架构:
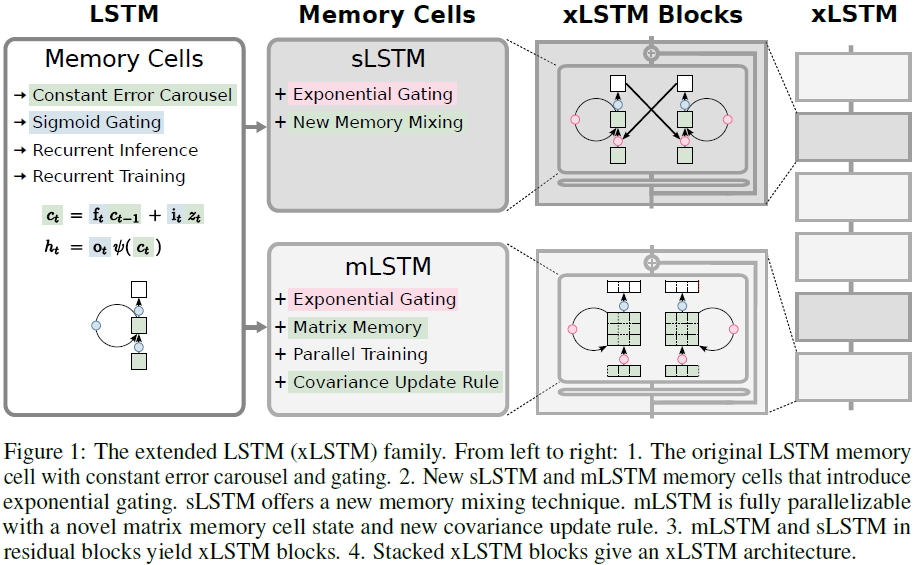
- 一个带有后上投影(post up-projection)的残差块(类似于Transformer),它在原始空间中非线性地总结过去,然后线性映射到高维空间,应用非线性激活函数,然后线性映射回原始空间;见图 3 的左侧面板和图 1 中的第三列。附录中的图 9 展示了更详细的版本。
- 一个带有前上投影(pre up-projection)的残差块(类似于 SSM),它线性映射到高维空间,然后在高维空间中非线性地总结过去,最后线性映射回原始空间。
对于包含 sLSTM 的 xLSTM 块,我们主要使用后向投影块。对于包含 mLSTM 的 xLSTM 块,我们使用预向投影块,因为在高维空间中的存储容量更大。有关更多细节,请参见图 3 的左侧面板和图 1 的第三列,或附录中的图 9。


图 9:sLSTM 块的示意图 - 后上投影(post up-projection):嵌入在 pre-LayerNorm 残差结构中,输入可以选择通过窗口大小为 4 的因果卷积进行传递,其中包括用于输入门和遗忘门的 Swish 激活。然后,对于所有输入、遗忘和输出门 i、f、o,以及单元更新 z,输入通过一个具有四个对角块或 “头” (Head)的对角线线性层。这些对角块与来自上一个隐藏状态的递归门 pre-activations 相一致,对应于一个具有四个头的 sLSTM,用圆形箭头表示。得到的隐藏状态通过一个 GroupNorm 层(Wu & He, 2018) - 对于每个头部的 LayerNorm。最后,输出通过一个门控 MLP 进行上下投影,使用 GeLU 激活函数和投影因子(PF) 4/3 来匹配参数。
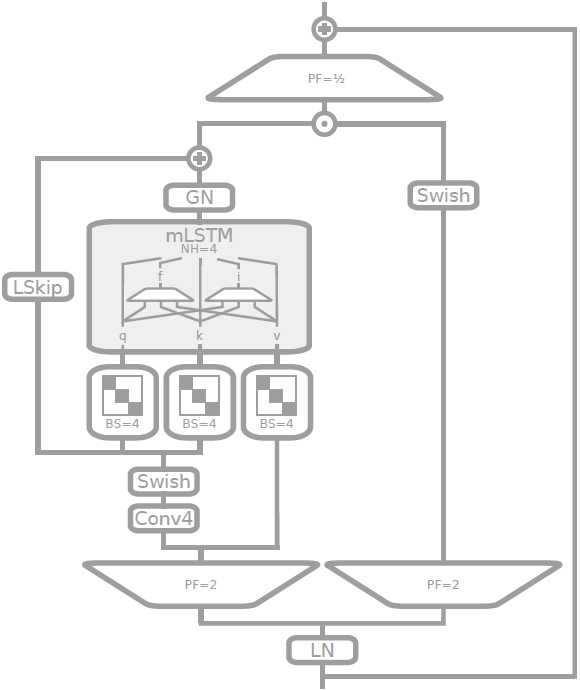
图10:mLSTM 块的示意图 - 前上投影(pre up-projection):嵌入在 pre-LayerNorm 残差结构中,首先对输入进行上投影,投影因子为 2,一次用于外部化输出门,一次作为 mLSTM 单元的输入。 mLSTM 单元的输入在维度方向上因果卷积(卷积核大小为4)之后,进入可学习的跳跃连接。我们通过块(Block)大小为 4 的块对角投影矩阵获得输入 q 和 k。值 v 直接馈送,跳过卷积部分。在 mLSTM 序列混合之后,通过 GroupNorm(Wu & He, 2018)进行输出归一化(对于每个头的 LayerNorm)。最后,将可学习的跳跃输入添加到结果中,并使用外部输出门对结果进行逐分量门控。然后进行下投影。

xLSTM 架构。xLSTM 架构是通过残差堆叠构建块(Srivastava等,2015; He等,2016)构建的。我们依赖于当代大型语言模型中最常用的 pre-LayerNorm(Ba等,2016b)残差主干。请参见图 1 中的最后一列。
2.5 内存和速度考虑
与 Transformer 相反,xLSTM 网络具有线性计算和与序列长度相对应的恒定内存复杂度。由于 xLSTM 内存具有压缩性,因此非常适合工业应用和在边缘上的实现。
mLSTM 的记忆不需要参数,但通过其 d×d 矩阵存储和 d×d 更新而在计算上昂贵。我们在内存容量与计算复杂性之间进行权衡。尽管如此,计算可以在 GPU 上并行进行,因此这些计算对墙上时钟时间(wall clock time)的影响很小。
虽然 mLSTM 类似于 FlashAttention(Dao等,2022; Dao,2024)或 GLA(Yang等,2023)可并行化,但由于内存混合(隐藏-隐藏连接),sLSTM 不可并行化。然而,我们开发了一个快速的 CUDA 实现,通过 GPU 内存优化到寄存器级别,通常比 mLSTM 慢不到两倍。
4. 实验
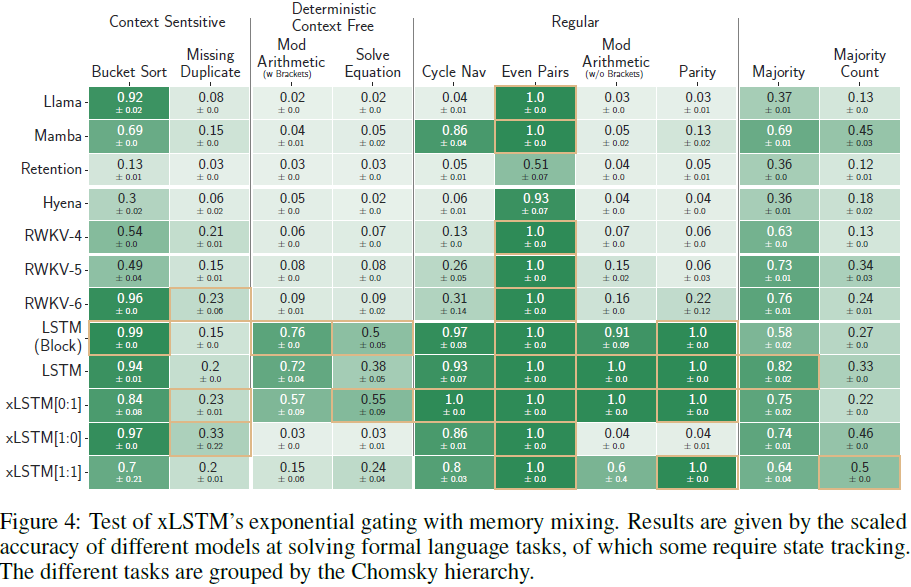
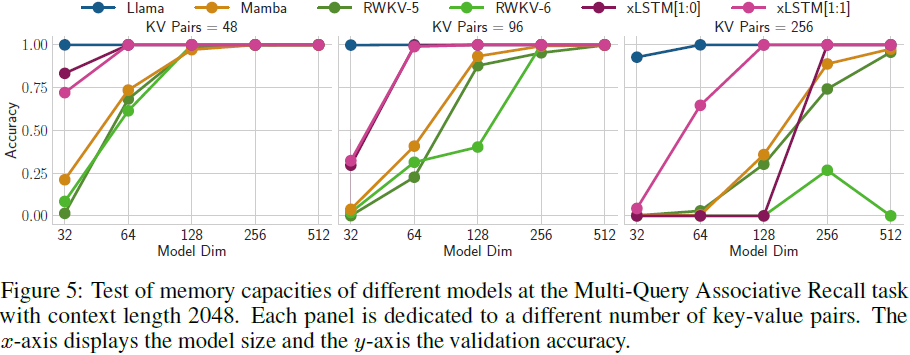
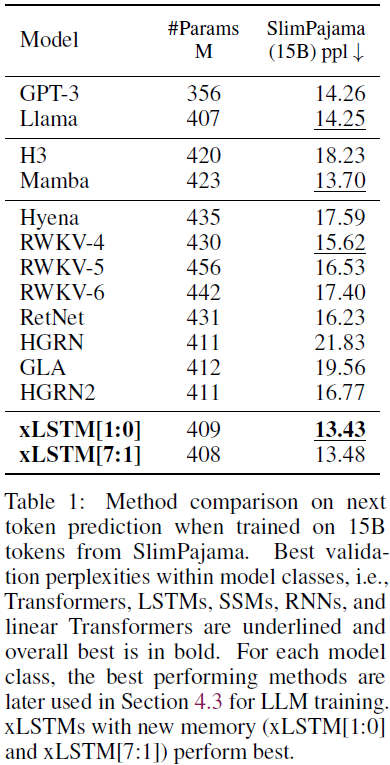
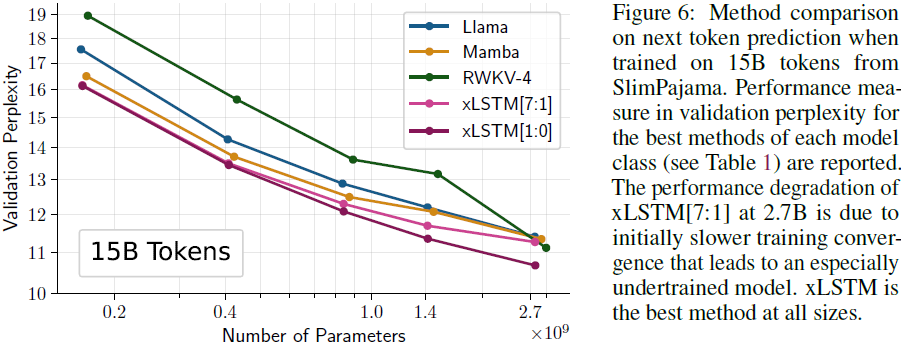
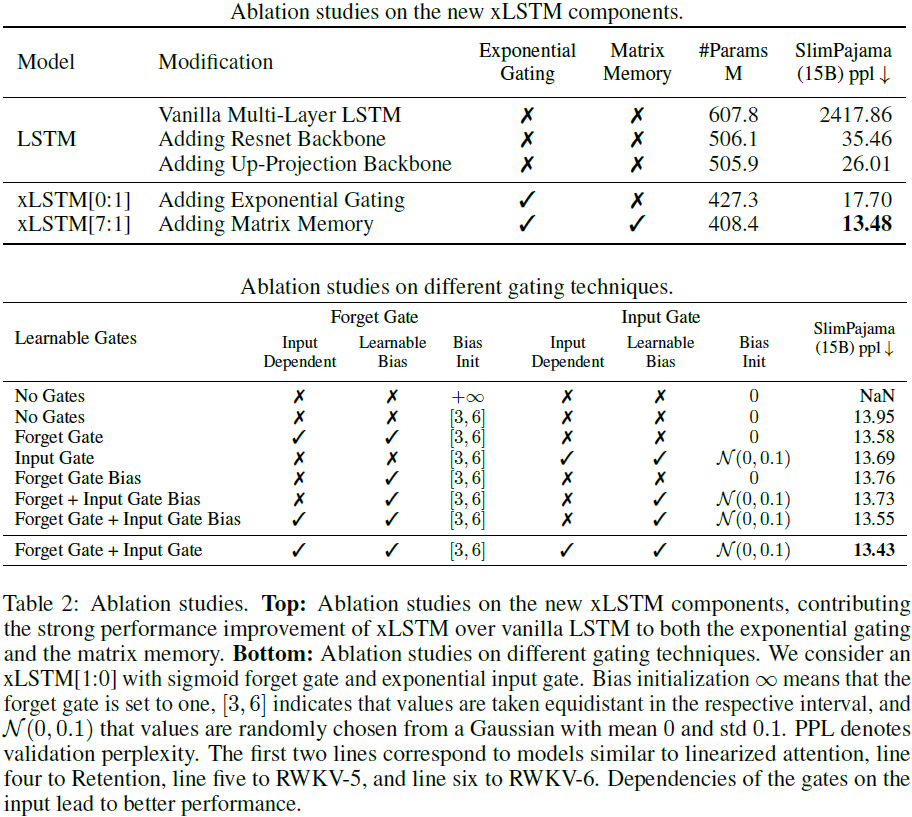
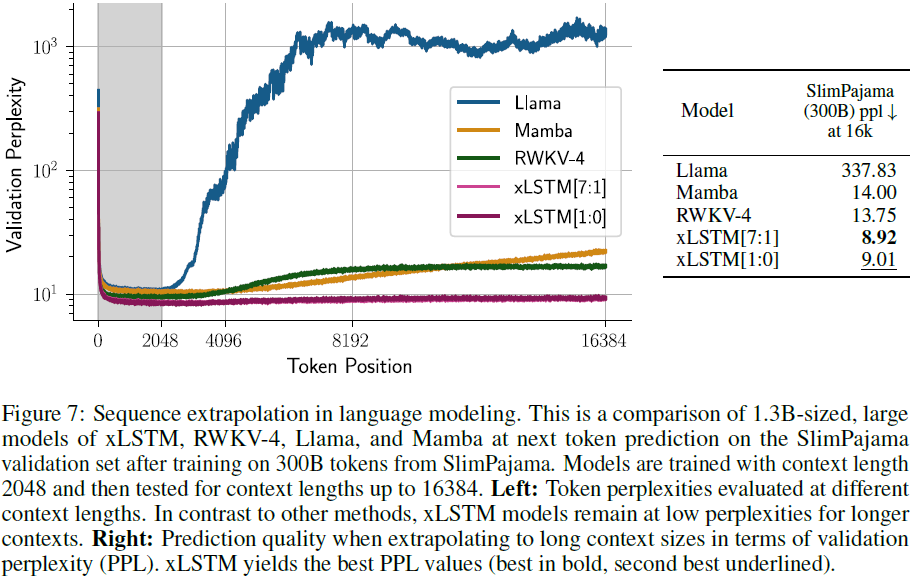
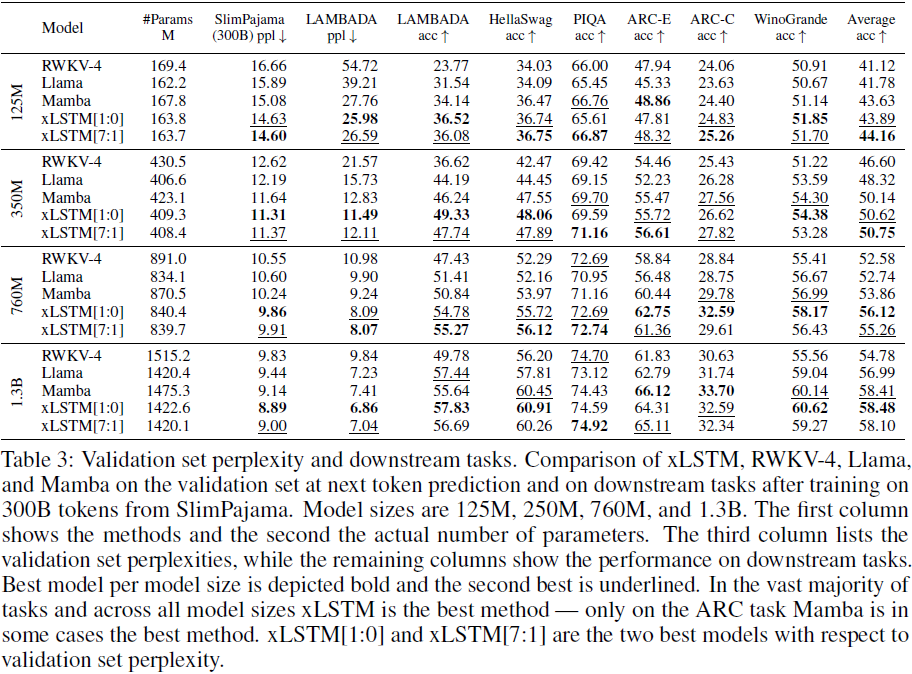
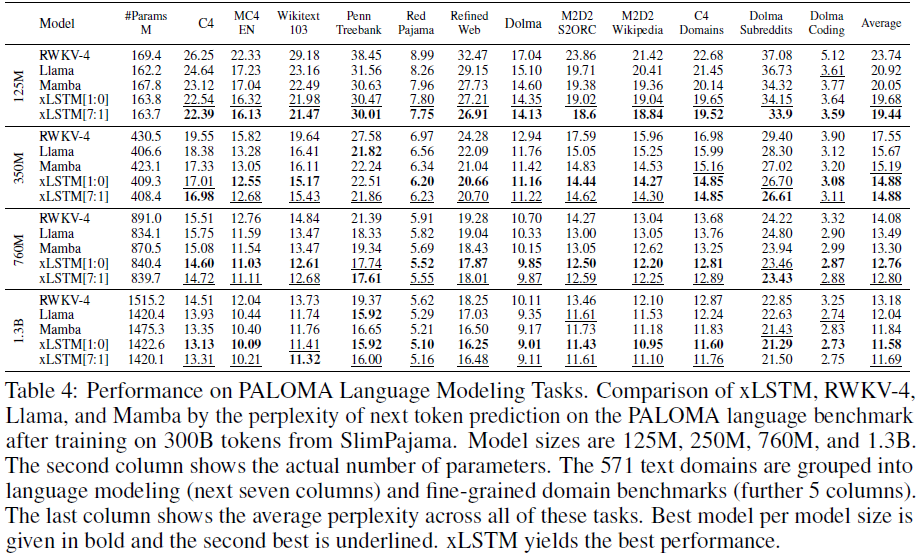
5. 限制
- 与 mLSTM 相比,sLSTM 的内存混合阻止了可并行化操作,因此不允许快速的并行实现。尽管如此,我们为 sLSTM 开发了一个快速的 CUDA 核心,目前的速度大约比我们的并行 mLSTM 实现慢了 1.5 倍左右。
- mLSTM 的 CUDA 核心尚未优化,因此当前的实现速度约为 FlashAttention 或 Mamba 中使用的扫描的 4 倍。可以通过类似于 FlashAttention 的方法获得更快的 CUDA 核心。
- 因为必须处理 d×d 矩阵,mLSTM 的矩阵内存具有较高的计算复杂性。尽管如此,内存的更新和检索不使用参数,并且可以使用标准矩阵操作进行并行化,因此由于复杂的内存而引起的墙上时钟时间开销很小。
- 遗忘门的初始化必须谨慎选择。
- 由于矩阵内存与序列长度有关(原论文中为无关,我认为应该是有关),增加序列长度可能会使较长上下文大小的内存超载。尽管如此,对于长达 16k 的上下文来说,这似乎并不是一个限制,参见第 4.3 节。
- 由于大型语言实验的昂贵计算负载,我们既没有完全优化架构,也没有优化超参数,特别是对于更大的 xLSTM 架构。我们预计,xLSTM 达到其全部潜力需要进行广泛的优化过程。
6. 结论
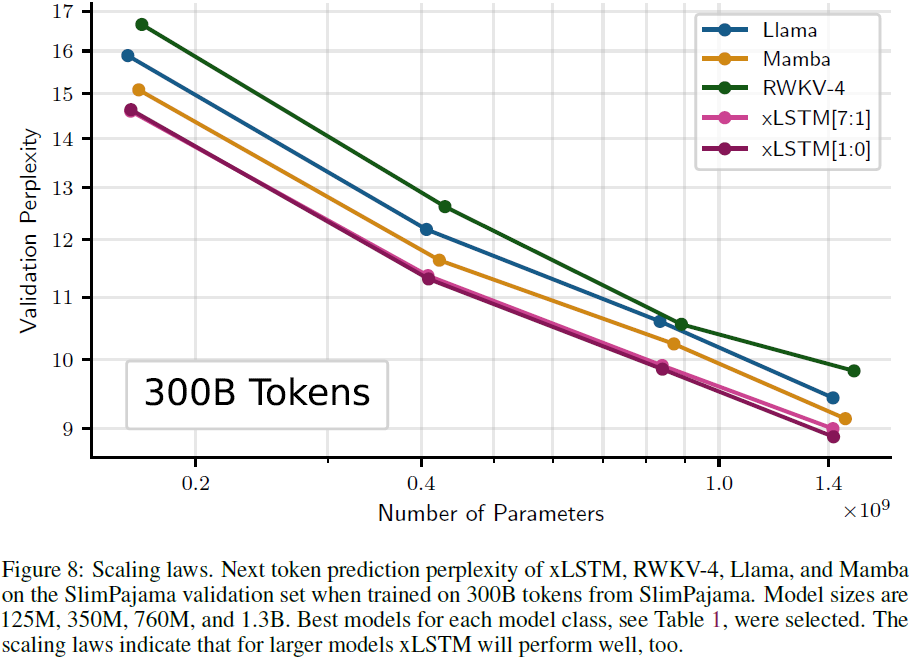
我们部分回答了我们的简单问题:将 LSTM 扩展到数十亿个参数时,我们能取得多远的语言建模进展?到目前为止,我们可以回答:“至少与当前的技术(如 Transformer 或 SSM)一样远”。我们通过指数门和内存混合以及新的内存结构将 LSTM 改进为 xLSTM。与 Transformer 和 SSM 等最新方法相比,xLSTM 模型在语言建模方面表现良好。扩展定律表明,更大的 xLSTM 模型将成为使用 Transformer 技术构建的当前大型语言模型的严肃竞争对手。xLSTM 有潜力对其他深度学习领域产生重大影响,如强化学习、时间序列预测或物理系统建模。



![[C++]哈希应用-布隆过滤器快速入门](https://img-blog.csdnimg.cn/direct/5368f3ff867f40d19a4766f05b5c287e.png#pic_center)