【题目来源】
https://www.luogu.com.cn/problem/P3391
【题目描述】
您需要写一种数据结构(可参考题目标题),来维护一个有序数列。 其中需要提供以下操作:翻转一个区间,例如原有序序列是 5 4 3 2 1,翻转区间是 [2,4] 的话,结果是 5 2 3 4 1。
【输入格式】
第一行两个正整数 n,m,表示序列长度与操作个数。序列中第 i 项初始为 i。 接下来 m 行,每行两个正整数 l,r,表示翻转的区间。 输出格式 输出一行 n 个正整数,表示原始序列经过 m 次变换后的结果。
【输出格式】
输出一行 n 个正整数,表示原始序列经过 m 次变换后的结果。
【输入样例】
5 3
1 3
1 3
1 4
【输出样例】
4 3 2 1 5
【数据范围】
对于 100% 的数据,1≤n,m≤100000,1≤l≤r≤n。
【算法分析】
Splay 树简介:https://blog.csdn.net/hnjzsyjyj/article/details/138504578
● Treap 树解决平衡的办法是给每个结点加上一个随机的优先级,实现概率上的平衡。Splay 树直接用旋转调整树的形态,通过旋转改善树的平衡性。计算量小,效果好。
● Splay 树的旋转主要分为“单旋”和“双旋”。
所谓“单旋”,即把结点 x 与它的父结点交换位置,使结点 x 上升一层。“单旋”不会减少树的层数,对改善平衡性没有帮助。根据旋转方向,“单旋”又分为左旋(zag)与右旋(zig)。
所谓“双旋”,即两次“单旋”。“双旋”同时旋转结点 x,父结点 f 及祖父结点 g 等3个结点,能改善平衡性。“双旋”又分为“一字旋”与“之字旋”。
● Splay 树的旋转示意图
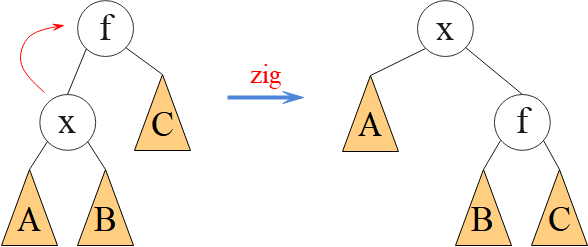

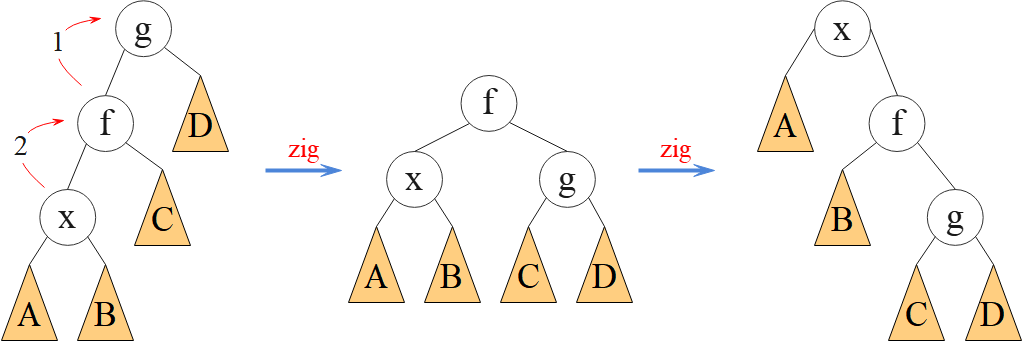
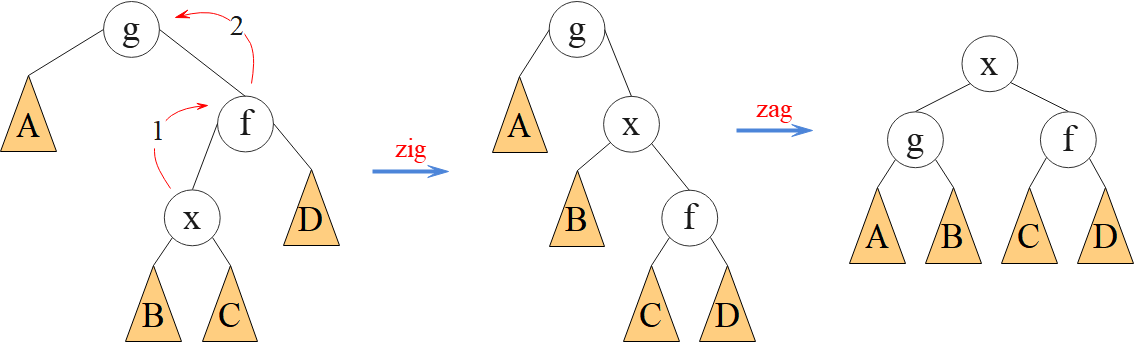
● Splay 树的基本操作是把结点旋转到树的根部,这样下次访问它时,只需查一次就 OK 了。
● Splay 树是动态树(LCT,Link Cut Tree)与树链剖分的基础。
● Splay 树曾经是最常使用的 BST。不过,现在经常使用 FHQ Treap 树实现很多传统的 Splay 树的题目。因为,FHQ Treap 树代码更容易写,效率也很高,且可做持久化。
【算法代码】
下面代码是 Splay 树的模板代码,但其中包含了本题(洛谷 P3391)未用的函数。例如:
本例使用了 pushup()、pushdown()、rotate()、splay()、insert()、get_val_by_pri() 、output() 等7个函数;未使用 find()、get_pre()、get_suc()、remove()、get_pri_by_val() 等5个函数。
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
int n,m;
int root,idx;
struct Node {
int s[2],v,p; //subtree,val,root
int size,cnt;
int lazy;
} tr[maxn];
void pushup(int x) {
tr[x].size=tr[tr[x].s[0]].size+tr[tr[x].s[1]].size+tr[x].cnt;
}
void pushdown(int x) {
if(tr[x].lazy) {
swap(tr[x].s[0],tr[x].s[1]);
tr[tr[x].s[0]].lazy^=1;
tr[tr[x].s[1]].lazy^=1;
tr[x].lazy=0;
}
}
void rotate(int x) {
int y=tr[x].p;
int z=tr[y].p;
int k=(tr[y].s[1]==x);
tr[z].s[tr[z].s[1]==y]=x, tr[x].p=z;
tr[y].s[k]=tr[x].s[k^1], tr[tr[x].s[k^1]].p=y;
tr[x].s[k^1]=y, tr[y].p=x;
pushup(y), pushup(x);
}
void splay(int x,int k) {
while(tr[x].p!=k) {
int y=tr[x].p;
int z=tr[y].p;
if(z!=k) {
if((tr[y].s[0]==x)^(tr[z].s[0]==y)) rotate(x);
else rotate(y);
}
rotate(x);
}
if(!k) root=x;
}
void insert(int x) {
int u=root, p=0;
while(u && tr[u].v!=x) {
p=u;
u=tr[u].s[x>tr[u].v];
}
if(u) tr[u].cnt++;
else {
u=++idx;
if(p) tr[p].s[x>tr[p].v]=u;
tr[u].p=p, tr[u].v=x, tr[u].size=1;
tr[u].cnt=1;
}
splay(u,0);
}
void find(int x) {
int u=root;
while(tr[u].s[x>tr[u].v] && tr[u].v!=x) u=tr[u].s[x>tr[u].v];
splay(u,0);
}
int get_pre(int x) {
find(x);
if(tr[root].v<x) return root;
int u=tr[root].s[0];
while(tr[u].s[1]) u=tr[u].s[1];
splay(u,0);
return u;
}
int get_suc(int x) {
find(x);
if(tr[root].v>x) return root;
int u=tr[root].s[1];
while(tr[u].s[0]) u=tr[u].s[0];
splay(u,0);
return u;
}
void remove(int x) {
int pre=get_pre(x), suc=get_suc(x);
splay(pre,0), splay(suc,pre);
int del=tr[suc].s[0];
if(tr[del].cnt>1) tr[del].cnt--, splay(del,0);
else tr[suc].s[0]=0, splay(suc,0);
}
int get_pri_by_val(int x) {
insert(x);
int ans=tr[tr[root].s[0]].size;
remove(x);
return ans;
}
int get_val_by_pri(int x) {
int u=root;
while(true) {
pushdown(u);
if(x<=tr[tr[u].s[0]].size) u=tr[u].s[0];
else if(x==tr[tr[u].s[0]].size+1) return u;
else x-=tr[tr[u].s[0]].size+1, u=tr[u].s[1];
}
return -1;
}
void output(int x) {
pushdown(x);
if(tr[x].s[0]) output(tr[x].s[0]);
if(1<=tr[x].v && tr[x].v<=n) printf("%d ",tr[x].v);
if(tr[x].s[1]) output(tr[x].s[1]);
}
int main() {
scanf("%d %d",&n,&m);
for(int i=0; i<=n+1; i++) insert(i);
while(m--) {
int le,ri;
scanf("%d%d",&le,&ri);
le=get_val_by_pri(le);
ri=get_val_by_pri(ri+2);
splay(le,0);
splay(ri,le);
tr[tr[ri].s[0]].lazy^=1;
}
output(root); //inorder
return 0;
}
/*
in:
5 3
1 3
1 3
1 4
out:
4 3 2 1 5
*/
【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/138504578
https://www.acwing.com/file_system/file/content/whole/index/content/6921304/
https://www.acwing.com/file_system/file/content/whole/index/content/6420964/






![[XR806开发板试用] XR806 调用cjson 实现数据序列化](https://img-blog.csdnimg.cn/direct/acff661d0f9a4225a2051a9464eacc07.png)