1.什么是汉诺塔问题

简单来说，就是有三个柱子，分别为A柱，B柱，C柱。其中A柱从上往下存放着从小到大的圆盘，我们需要借助B柱和C柱，将A柱上的所有圆盘转移到C柱上，并且一次只能移动一个圆盘，且在移动的过程中，大圆盘不能再小圆盘的上面。

2.思路分析

首先，我们的最终目的是将A柱上的圆盘全部转移到C柱上。则当A柱上只有一个圆盘，我们直接将A柱上的圆盘转移到C柱上就行了。

如下图所示

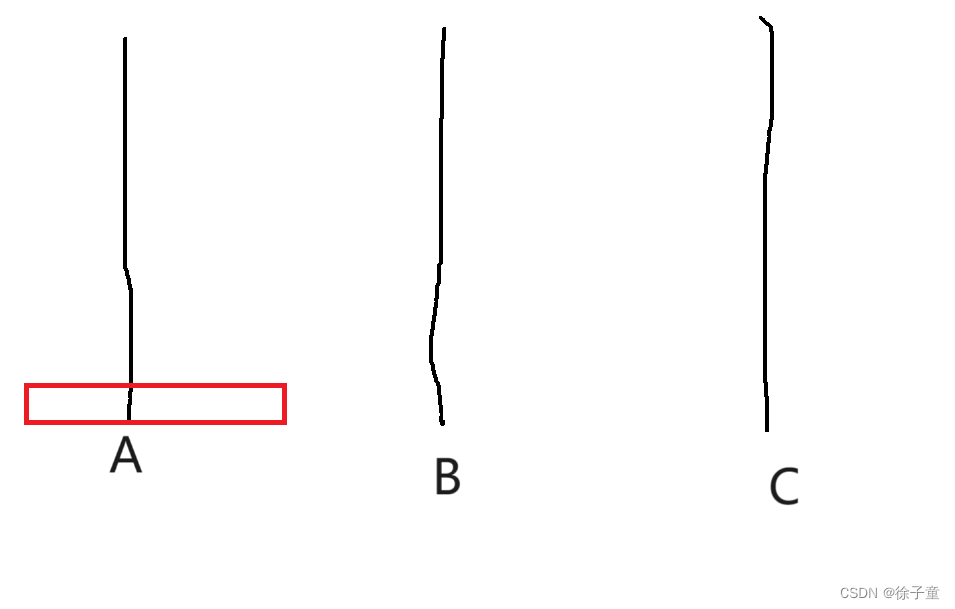
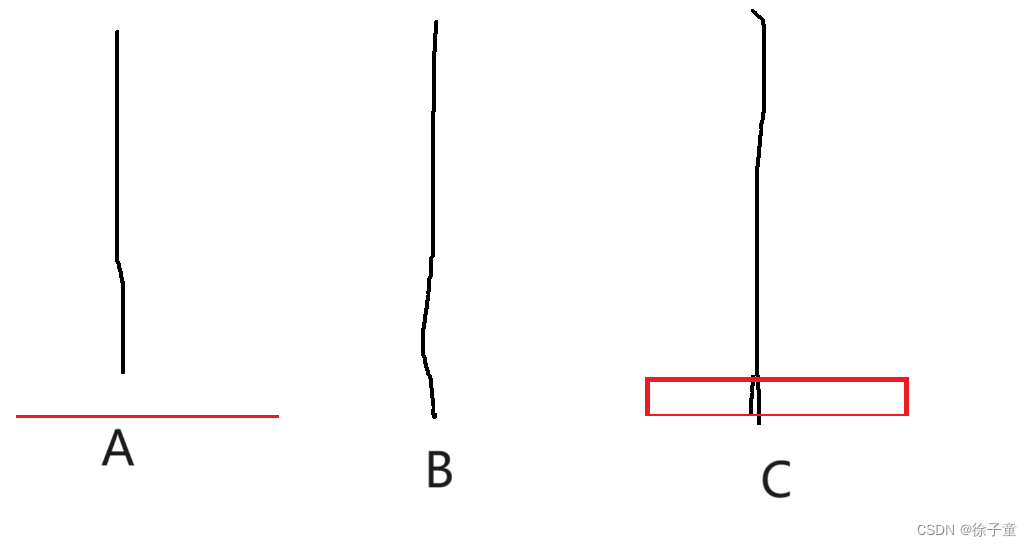
当A柱上有多个圆盘时，就很复杂了，我们需要慢慢来分析。

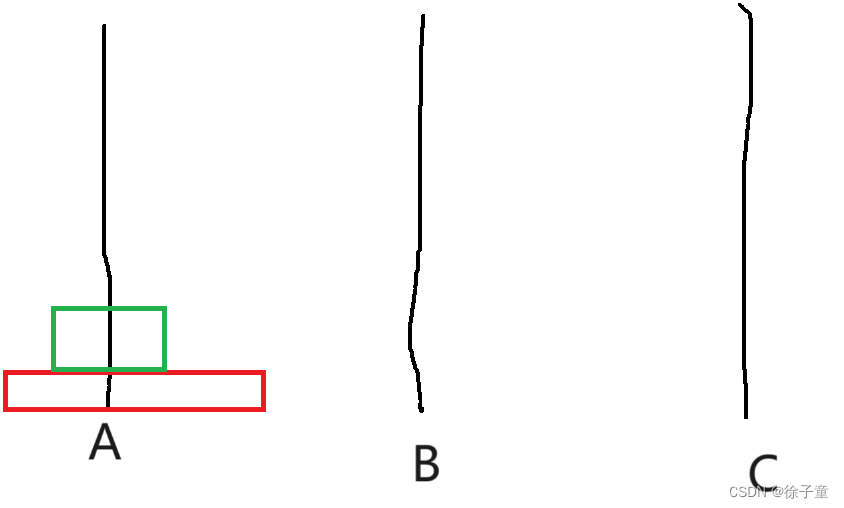
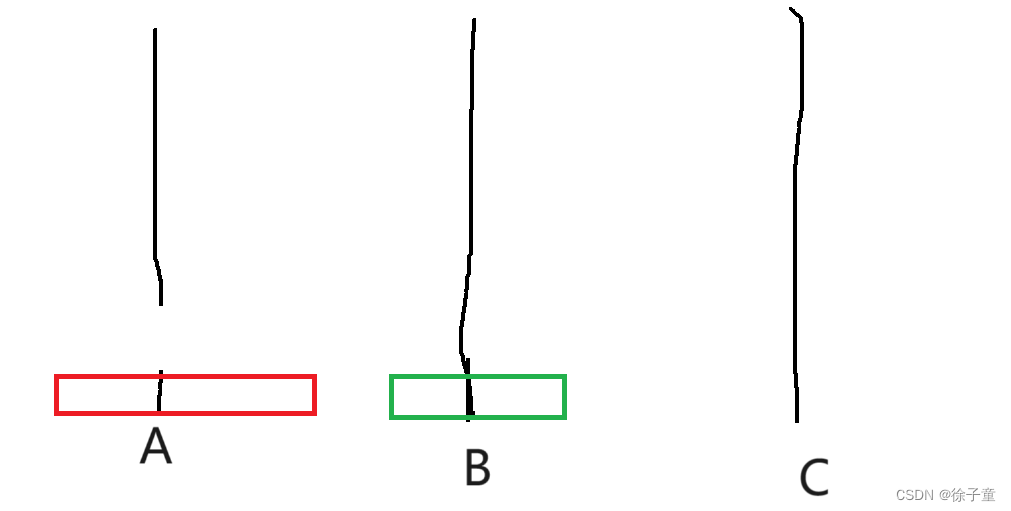
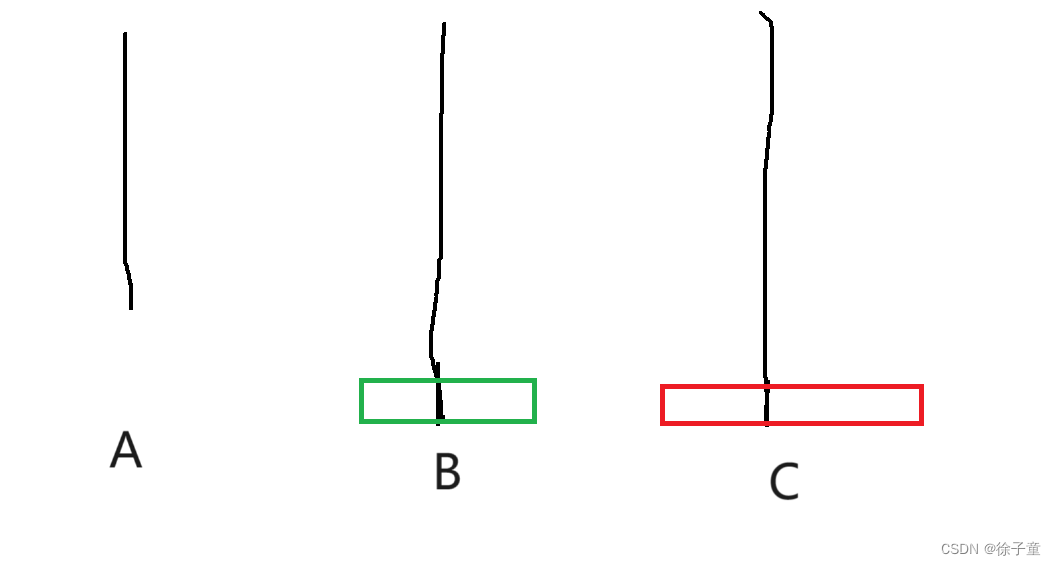
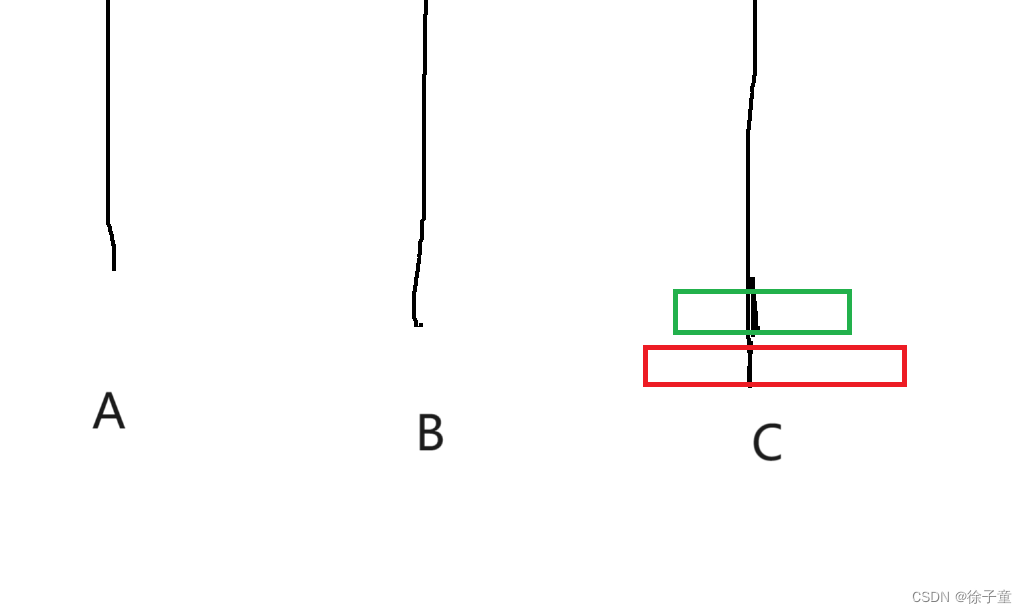
当A柱上有2个圆盘时。我们要先将第一个圆盘转移到B柱上，然后再将第二个圆盘转移到C柱上，然后再将B柱上的圆盘转移到C柱上。

简化为 A->B   A->C   B->C。

如下图所示

当有3个圆盘时。

我们先将A盘上的第一个盘子转移到C柱，再将A柱上的第二个圆盘转移到B柱上，接着再将C盘上的圆盘转移到B柱上，再将A柱上的最后一个圆盘转移到C柱上，接着再将B柱上的第一个圆盘转移到A柱上，再将B柱上的最后一个圆盘转移到C柱上，接着再将A柱上的圆盘转移到C柱上，就完成了。

简化来说，A->C   A->B   C->B  A->C   B->A  B->C   A->C。

如下图所示  

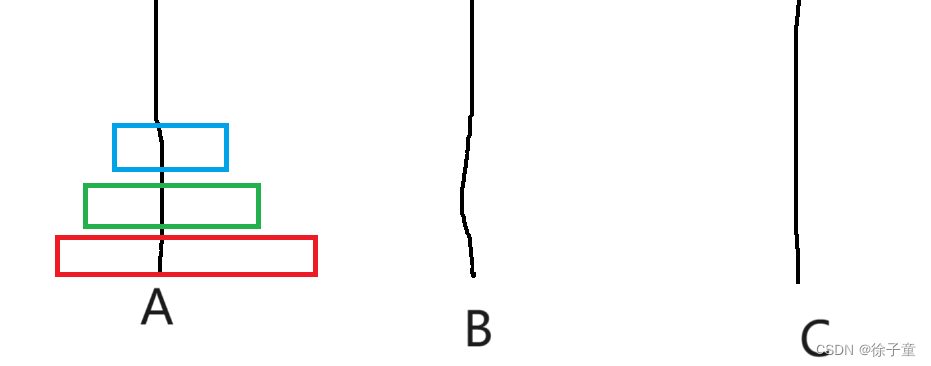
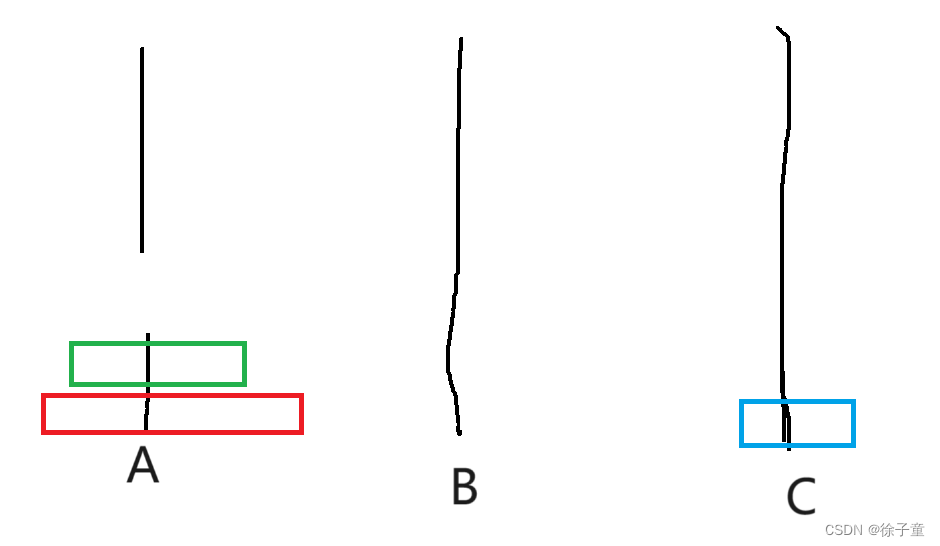
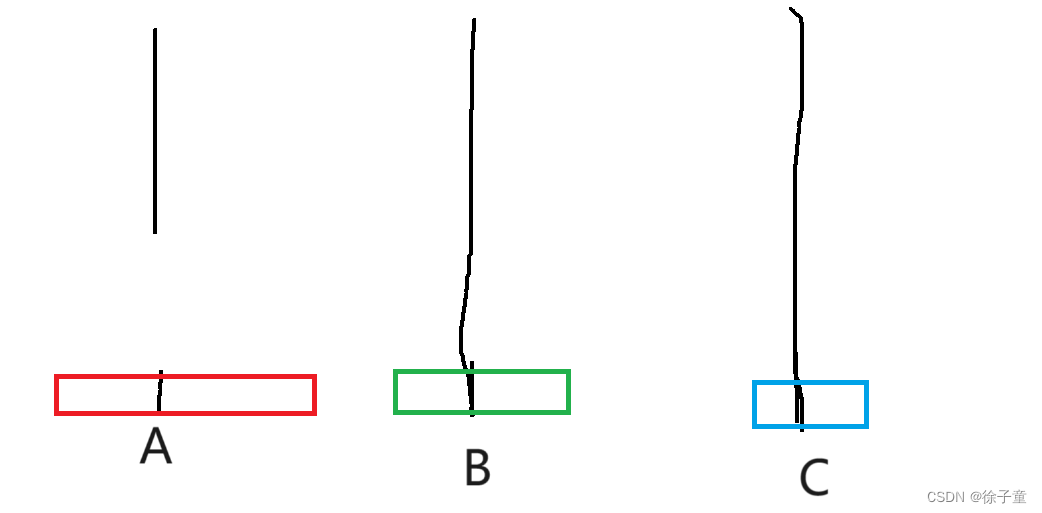
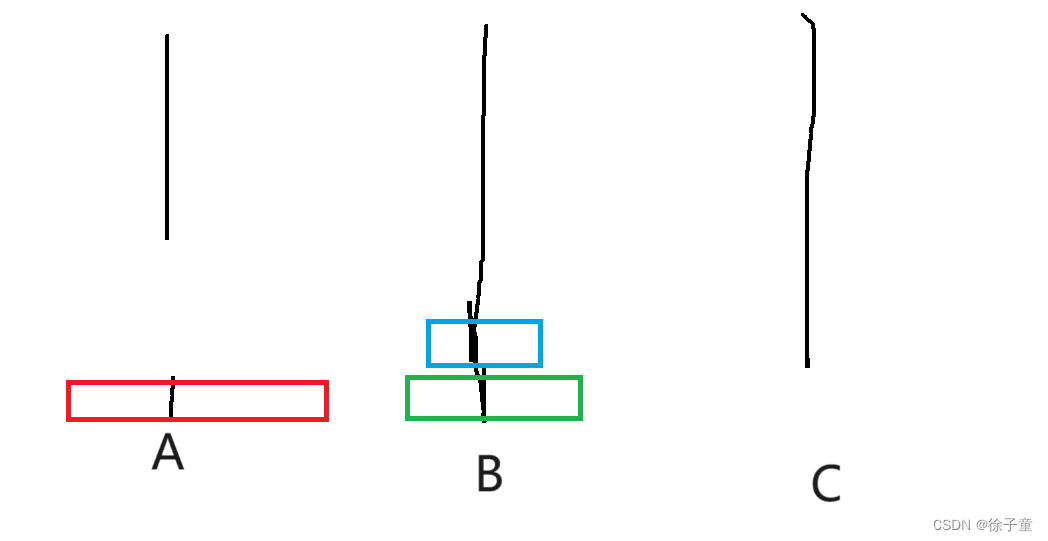
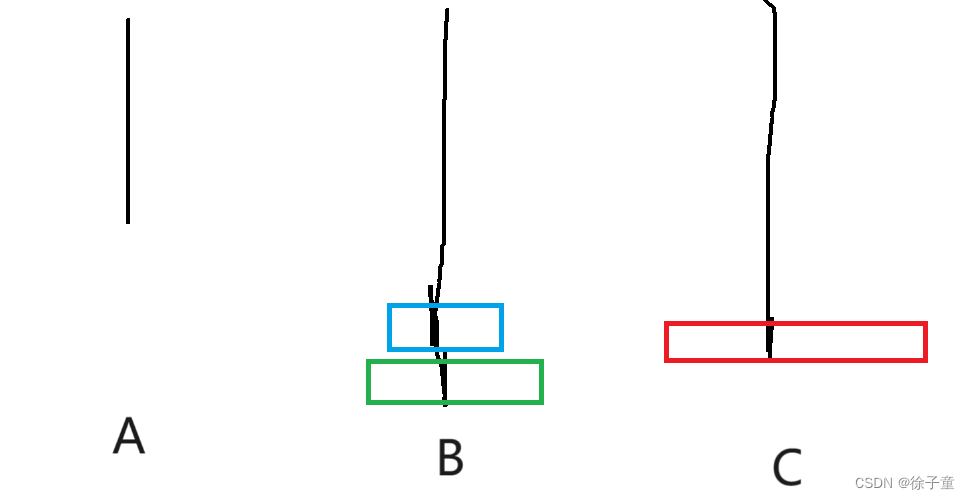
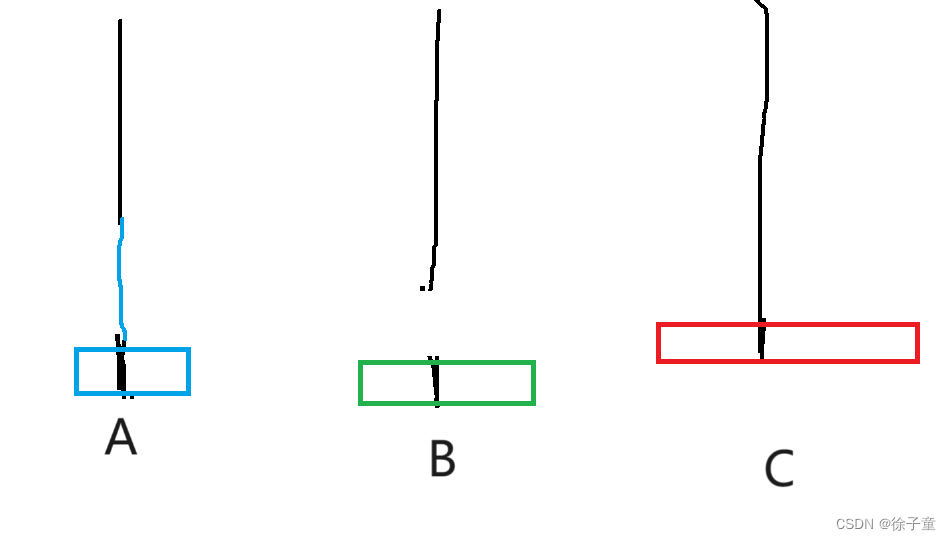
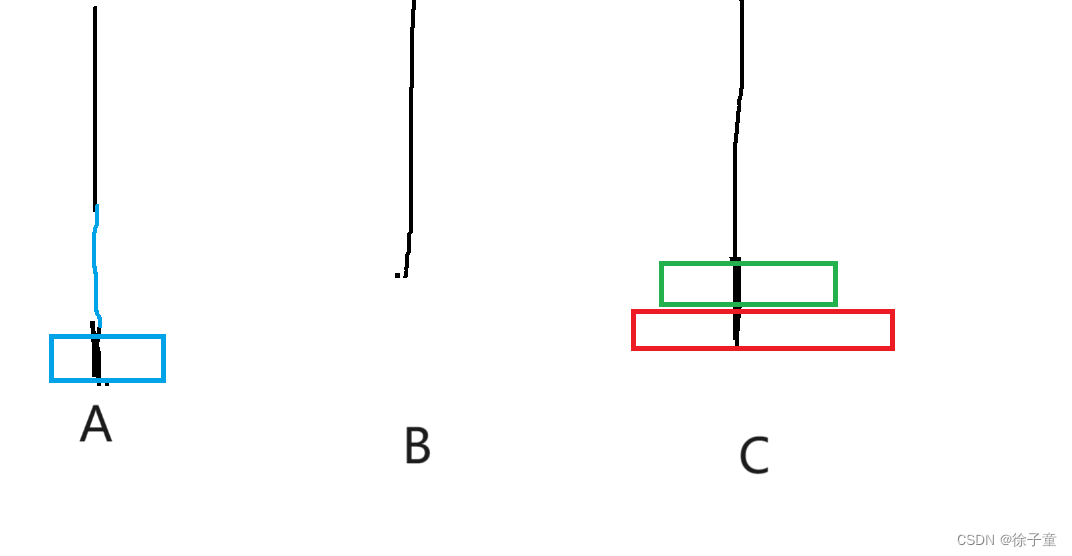
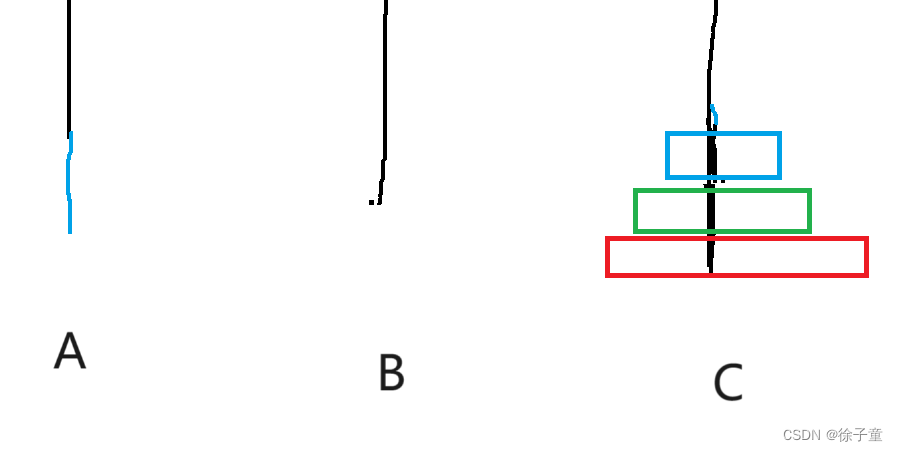
 通过2个圆盘和3个圆盘的例子发现，要向将A柱上的圆盘按要求转移到C柱上，我们要将n-1个圆盘全部转移到B柱上。

代码实现

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int count = 0;//全局变量做计数器
void move(char Tower_1, char Tower_2)
{
	printf("将 %c 移动到 %c \n", Tower_1, Tower_2);
	count++;
}
void Hanoi(int n, char Tower_1, char Tower_2, char Tower_3)
{
	if (n == 1)
		//是一个的话就直接从Tower_1移动到Tower_3
		move(Tower_1, Tower_3);
	else
	{
		//不是一个的话先借助Tower_3将Tower_1上面的n-1个移动到Tower_2
		Hanoi(n - 1, Tower_1, Tower_3, Tower_2);
		//完成此过程后Tower_1上面还有最后一个 
		move(Tower_1, Tower_3); //将Tower_1上面的最后一个移动到Tower_3
		//将Tower_2上面的n-1个通过Tower_1移动到Tower_3
		Hanoi(n - 1, Tower_2, Tower_1, Tower_3);
	}
}
int main()
{
	printf("请输入圆盘个数:\n");
	int n = 0;
	scanf("%d", &n);
	Hanoi(n, 'A', 'B', 'C');
	printf("一共进行了%d次", count);
	return 0;
}

汉诺塔问题涉及到了递归的的问题，其里面有两个递归的过程，其实十分复杂的。