5.6.1 KMP算法中next值的计算
设模式的长度为m。用蛮力法求解 KMP算法中的 next值时,next[0]可直接给出,计算next[j](1<=j<=m-1)则需要在 T[0] …T[j-1]中分别取长度为j-1、..、2、1的真前缀和真后缀并比较是否相等,最坏情况下的时间代价是: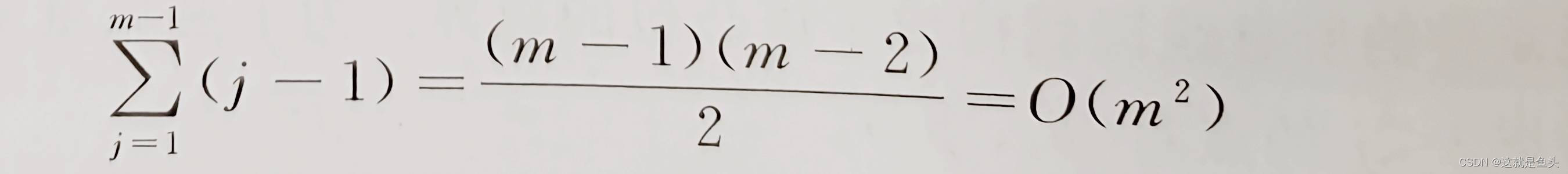
但实际上,只需将模式扫描一遍,就能够在线性时间内求得模式的next值。
因为T[0]既没有真前缀也没有真后缀,因此 next[0]=-1。假设已经计算出next[0],next[1],...,next[j], 如何计算 next[j+1]呢?设 k=next[j], 则 T[0]...T[k-1]=T[j-k]...T[j-1],这意味着 T[0]...T[k-1]是T[0]···T[j-1]的真前缀,同时 T[j-k]...T[j-1]是 T[0]...T[j-1]的真后缀。为了计算 next[j+1],比较 T[k]和T[j],可能出现两种情况:
(1) T[k]=T[j]:说明 T[0]~T[k-1]T[k]=T[j-k]~T[j-1]-T[j], 如图5-15所示。由next值的义,next[j+1]=k+1。
(2) T[k]≠T[j]:此时要找出 T[0]...T[j-1]的真前缀和真后缀相等的第2大子串,由
于T[0]...T[j-1]的真前缀和真后缀相等的最大子串是 T[0]...T[k-1], 而 next[k]的值为T[0].…T[k一1]的真前缀和真后缀相等的最大子串的长度,则 T[0].…T[next[k]-1]即T[0]...T[j-1]的真前缀和真后缀相等的第2大子串,如图5-16所示。令 k=next[k], 再比较T[k]和T[j],此时仍会出现两种情况。当T[k]=T[j]时,与情况(1)类似,此时,next[j+1]=k+1;当T[k]≠T[j]时, 与情况(2)类似,再找出 T[0]...T[k-1]的真前级和真后级相等的最大子串,重复(2)的过程,直至 T[k]=T[j],或 next[k]=-1, 说明T[0]..…T[j-1]不存在真前缀和真后缀相等的子串,此时,next[j+1]=0.

例如,模式 T="abaababc"的next值计算如下。
j=0时,next[0]=-1
j=1时,k=next[0]=-1, next[1]=0
j=2时, k=next[1]=0, T[0]≠T[1];k=next[k]=next[0]=-1.next[2]=0
j=3时,k=next[2]=0, T[0]=T[2]; next[3]=k+1=0+1=1
j=4时, k=next[3]=1, T[1]≠T[3];k=next[k]=next[1]=0, T[0]=T[3], next[4]=k+1=1
j=5时,k=next[4]=1, T[1]=T[4],next[5]=k+1=1+1=2
j=6时,k=next[5]=2, T[2]=T[5],next[6]=k+1=2+1=3
j=7时, k=next[6]=3, T[3]≠T[6];k=next[k]=next[3]=1, T[1]=T[6], next[7]=k+1=2
基于以上想法,在线性时间内求得模式next值的程序如下。
void GetNext(char T[ ], int next[]){
int j= 0,k=-1;
next[0]=-1;
while (T[j]!='\0')
{
if (k== -1) {next[++j]= 0;k=0;}
else if (T[j] == T[k])
{
k++;next[++j]= k;
}
else k= next[k];
}
}
5.6.2 0/1 背包问题
【问题】给定几个重量为(w1,w2, .…,wn)、价值为(V1,V2,...,Vn)的物品和一个容量为C的背包,0/1背包问题(0/1 knapsack problem)是求这些物品的一个最有价值的子集,并且要能够装到背包中。
应用实例
有几项可投资的项目,每个项目需要投入资金si,可获利润为Vi,现有可用资金总数为M,应选择哪些项目来投资,可获得最大利润。
【想法】用蛮力法解决0/1背包问题,需要考虑给定n个物品集合的所有子集,找出有总重量不超过背包容量的子集,计算每个可能子集的总价值,然后找到价值最大的子集。例如,给定4个物品的重量为(7,3,4,5),价值为(42, 12,40,25),和一个容量为10的背包,表5-3给出了蛮力法求解0/1背包问题的过程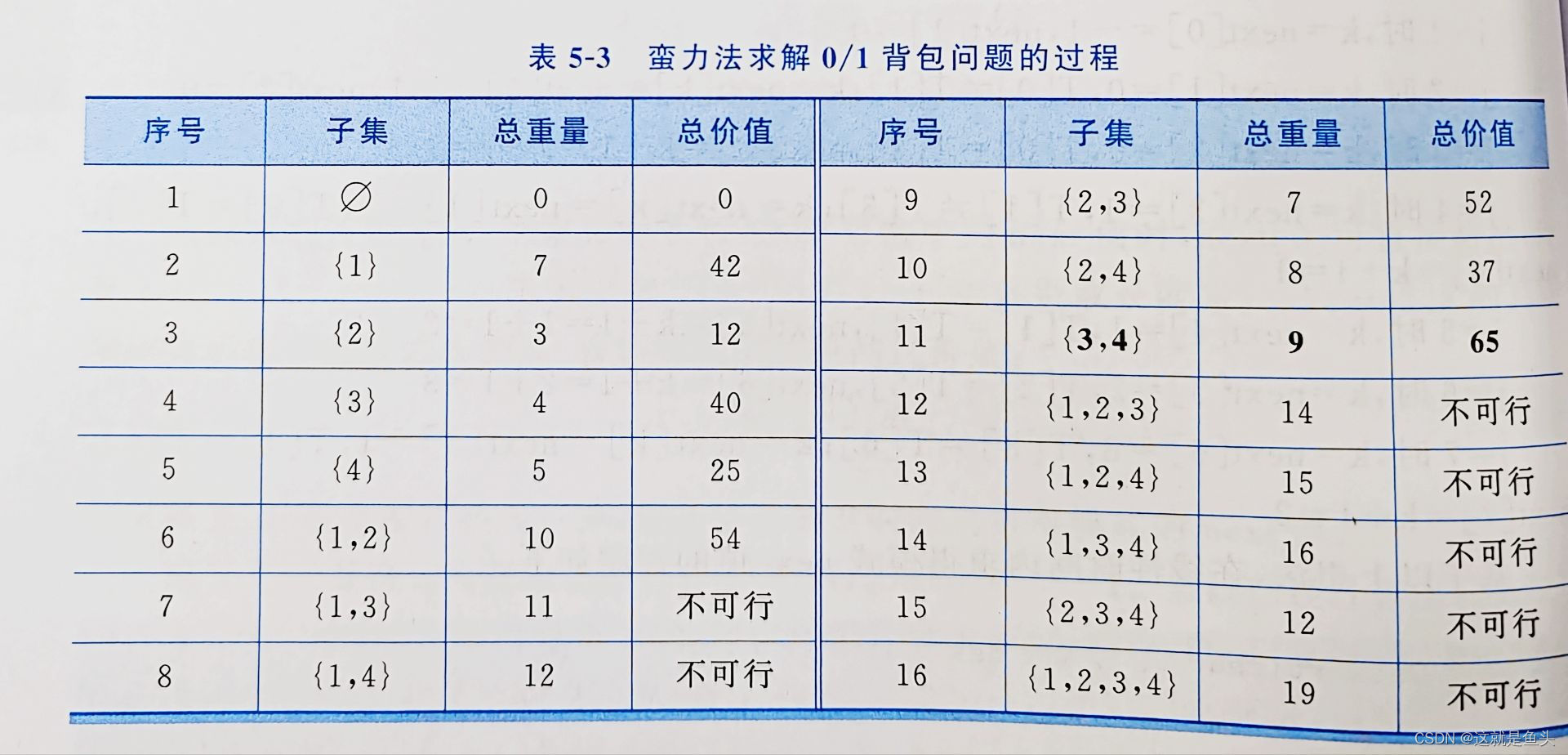
【算法】 蛮力法求解0/1背包问题的算法用伪代码描述如下。
算法:蛮力法求解 0/1 背包问题
输人:重量(W1, W2, …,Wn),价值(V1, V2,…,Vn),背包容量C
输出:装人背包的物品编号
1. 初始化最大价值 maxValue=0;结果子集S=非空;
2.对集合(1,2, …,n)的每一个子集T,执行下述操作:
2.1 初始化背包的价值value=0;背包的重量 weight=0;
2.2对子集T的每一个元素j执行下述操作:
2.2.1如果 weight+wj < C, 则 weight= weight+ wj, value=value+vj ;
2.2.2 否则,转步骤2考查下一个子集;
2.3 如果 maxValue < value, 则 maxValue=value; S=T;
3.输出子集S中的各元素;
【算法分析】 对于具有n个元素的集合,其子集数量是2^n,所以,无论生成子集的算
法效率有多高,蛮力法求解0/1背包问题的时间下限是Ω(2^n)。