1路径总和 II
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:
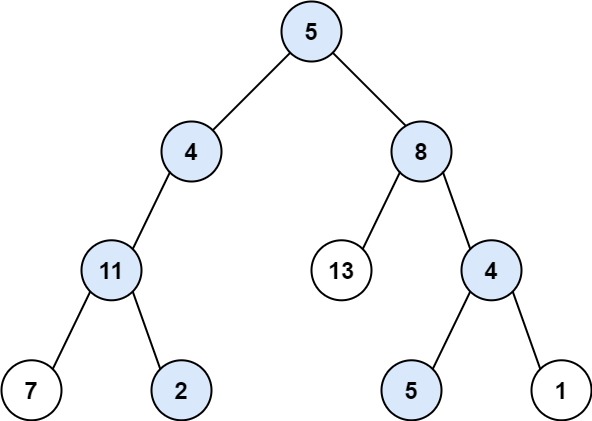
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:[[5,4,11,2],[5,8,4,5]]
示例 2:
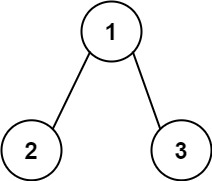
输入:root = [1,2,3], targetSum = 5 输出:[]
示例 3:
输入:root = [1,2], targetSum = 0 输出:[]
提示:
- 树中节点总数在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
思路:
.路径总和ii要遍历整个树,找到所有路径,所以递归函数不要返回值
-
定义数据结构:首先定义了一个
Solution类,其中包含了私有成员变量result和path,分别用于存放最终结果和当前路径。 -
递归遍历:通过递归方式遍历二叉树的每个节点,从根节点开始向下遍历。递归函数
traversal的参数包括当前节点指针cur和距离目标和还剩余的count。 -
叶子节点检查:在递归过程中,如果当前节点是叶子节点且剩余目标和
count为 0,说明找到了一条满足条件的路径,将该路径添加到结果中。 -
路径更新与回溯:在遍历过程中,将经过的节点值添加到
path数组中,同时更新剩余目标和count。然后递归遍历左右子树。在递归返回后,需要回溯,即将最后一个节点值移出path数组,以便尝试其他路径。 -
路径总和函数:
pathSum函数是对递归遍历的入口函数,首先清空之前的结果和路径,然后将根节点的值加入初始路径,并调用traversal函数开始递归遍历。
代码:
// 定义 Solution 类
class Solution {
private:
vector<vector<int>> result; // 存放最终结果的二维数组
vector<int> path; // 存放当前路径的节点值的一维数组
// 递归遍历函数,参数为当前节点指针 cur 和距离目标和还剩余的 count
void traversal(TreeNode* cur, int count) {
// 如果当前节点是叶子节点且 count 等于 0,将当前路径添加到结果中
if (cur->left == nullptr && cur->right == nullptr && count == 0) {
result.push_back(path);
return;
}
// 递归遍历左子树
if (cur->left) {
path.push_back(cur->left->val); // 将左子节点值加入路径
count -= cur->left->val; // 更新剩余目标和
traversal(cur->left, count); // 递归遍历左子树
count += cur->left->val; // 恢复剩余目标和
path.pop_back(); // 移除最后一个节点值,回溯
}
// 递归遍历右子树
if (cur->right) {
path.push_back(cur->right->val); // 将右子节点值加入路径
count -= cur->right->val; // 更新剩余目标和
traversal(cur->right, count); // 递归遍历右子树
count += cur->right->val; // 恢复剩余目标和
path.pop_back(); // 移除最后一个节点值,回溯
}
}
public:
// 求解路径总和的函数,参数为根节点指针 root 和目标和 targetSum
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
result.clear(); // 清空之前的结果
path.clear(); // 清空之前的路径
if (root == nullptr) return result; // 如果根节点为空,直接返回空结果
path.push_back(root->val); // 将根节点的值加入初始路径
traversal(root, targetSum - root->val); // 调用递归遍历函数
return result; // 返回结果数组
}
};2从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:

输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] 输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1] 输出:[-1]
提示:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder和postorder都由 不同 的值组成postorder中每一个值都在inorder中inorder保证是树的中序遍历postorder保证是树的后序遍历
思路:
一层一层切割,就应该想到了递归。
一共分以下几步:
-
如果数组大小为零的话,说明是空节点了。
-
如果不为空,那么取后序数组最后一个元素作为节点元素。
-
如果当前节点是叶子节点(后序数组大小为1),直接创建该节点并返回。
-
找到当前节点在中序遍历数组中的位置,以此位置作为左右子树的分界点。
-
切割中序遍历数组,得到左子树和右子树的中序数组。
-
舍弃后序遍历数组末尾元素,因为这个元素作为当前节点。
-
根据左子树中序数组的大小,切割后序遍历数组,得到左子树和右子树的后序数组。
-
递归构建左子树和右子树。
-
将左子树和右子树连接到当前节点的左右孩子上。
代码的解题思路:
-
递归函数:
traversal函数是一个递归函数,用于构建二叉树。它接受两个参数:inorder是中序遍历数组,postorder是后序遍历数组。 -
基准情况: 如果后序遍历数组为空,说明当前子树为空,直接返回空指针。
-
根节点: 后序遍历数组的最后一个元素是当前子树的根节点。在每次递归调用中,我们取出后序遍历数组的最后一个元素作为当前子树的根节点,并创建一个
TreeNode对象。 -
叶子节点: 如果后序遍历数组的大小为 1,说明当前节点是叶子节点,直接返回当前节点。
-
中序遍历中的根节点位置: 我们在中序遍历数组中找到根节点的位置,以便将中序数组分割为左子树和右子树。
-
切割中序数组: 使用根节点在中序遍历数组中的位置来切割中序数组,以得到左子树和右子树的中序遍历数组。
-
舍弃后序遍历数组末尾元素: 后序遍历数组的最后一个元素是根节点,所以在递归调用左右子树构建后,我们需要舍弃后序遍历数组的末尾元素,以便构建左右子树。
-
切割后序数组: 使用左子树的中序数组的大小来切割后序数组,以得到左子树和右子树的后序遍历数组。
-
递归构建左右子树: 分别对左子树和右子树进行递归调用,构建左右子树,并将它们分别连接到当前节点的左右孩子。
-
主函数:
buildTree是主函数,用于检查输入数组的有效性,并调用traversal函数来构建整个二叉树。
代码:
class Solution {
private:
// 定义递归函数,用于构建二叉树
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
// 如果后序遍历数组为空,返回空指针
if (postorder.size() == 0) return NULL;
// 后序遍历数组最后一个元素,即当前子树的根节点值
int rootValue = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootValue);
// 如果当前节点是叶子节点,直接返回该节点
if (postorder.size() == 1) return root;
// 找到当前根节点在中序遍历数组中的位置
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// 切割中序数组,左闭右开区间:[0, delimiterIndex)
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
// [delimiterIndex + 1, end)
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
// 舍弃后序遍历数组末尾元素,因为该元素是当前树的根节点
postorder.resize(postorder.size() - 1);
// 切割后序数组
// 依然左闭右开,使用左中序数组大小作为切割点
// [0, leftInorder.size)
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
// [leftInorder.size(), end)
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
// 递归构建左右子树
root->left = traversal(leftInorder, leftPostorder);
root->right = traversal(rightInorder, rightPostorder);
return root;
}
public:
// 主函数,用于构建二叉树
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
// 如果中序遍历数组或后序遍历数组为空,返回空指针
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
// 调用递归函数
return traversal(inorder, postorder);
}
};3合并二叉树
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:
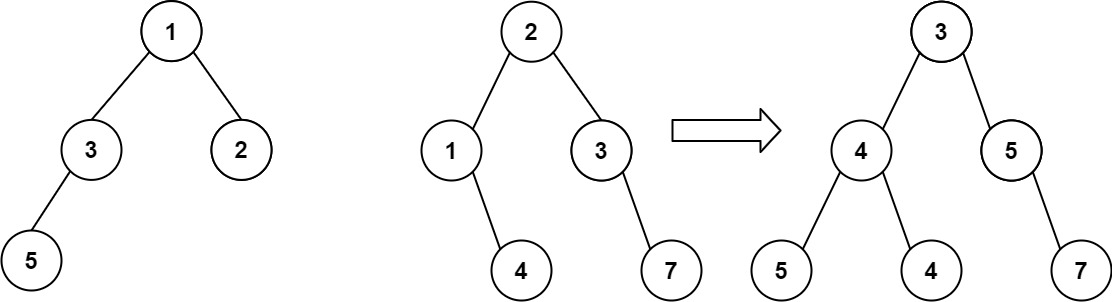
输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7] 输出:[3,4,5,5,4,null,7]
示例 2:
输入:root1 = [1], root2 = [1,2] 输出:[2,2]
提示:
- 两棵树中的节点数目在范围
[0, 2000]内 -104 <= Node.val <= 104
思路:
-
递归函数:
mergeTrees函数是一个递归函数,用于合并两棵二叉树。它接受两个参数root1和root2,分别表示两棵待合并的二叉树的根节点。 -
基准情况: 如果
root1为空,说明第一棵树为空,直接返回root2;如果root2为空,说明第二棵树为空,直接返回root1。 -
递归合并左子树和右子树: 对于当前节点,递归地合并它们的左子树和右子树,分别调用
mergeTrees函数,将合并后的左子树和右子树连接到当前节点的左孩子和右孩子上。 -
合并当前节点的值: 将两棵树当前节点的值相加,并更新到
root1节点上。 -
返回根节点: 返回合并后的第一棵树的根节点
root1。
代码:
class Solution {
public:
// 合并两棵二叉树
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
// 如果第一棵树为空,返回第二棵树
if (root1 == nullptr) return root2;
// 如果第二棵树为空,返回第一棵树
if (root2 == nullptr) return root1;
// 递归合并左子树
root1->left = mergeTrees(root1->left, root2->left);
// 递归合并右子树
root1->right = mergeTrees(root1->right, root2->right); // 修正此处的错误
// 合并当前节点的值
root1->val += root2->val;
// 返回合并后的第一棵树的根节点
return root1;
}
};4按日期分组销售产品
SQL Schema
Pandas Schema
表 Activities:
+-------------+---------+ | 列名 | 类型 | +-------------+---------+ | sell_date | date | | product | varchar | +-------------+---------+ 该表没有主键(具有唯一值的列)。它可能包含重复项。 此表的每一行都包含产品名称和在市场上销售的日期。
编写解决方案找出每个日期、销售的不同产品的数量及其名称。
每个日期的销售产品名称应按词典序排列。
返回按 sell_date 排序的结果表。
结果表结果格式如下例所示。
示例 1:
输入:
Activities 表:
+------------+-------------+
| sell_date | product |
+------------+-------------+
| 2020-05-30 | Headphone |
| 2020-06-01 | Pencil |
| 2020-06-02 | Mask |
| 2020-05-30 | Basketball |
| 2020-06-01 | Bible |
| 2020-06-02 | Mask |
| 2020-05-30 | T-Shirt |
+------------+-------------+
输出:
+------------+----------+------------------------------+
| sell_date | num_sold | products |
+------------+----------+------------------------------+
| 2020-05-30 | 3 | Basketball,Headphone,T-shirt |
| 2020-06-01 | 2 | Bible,Pencil |
| 2020-06-02 | 1 | Mask |
+------------+----------+------------------------------+
解释:
对于2020-05-30,出售的物品是 (Headphone, Basketball, T-shirt),按词典序排列,并用逗号 ',' 分隔。
对于2020-06-01,出售的物品是 (Pencil, Bible),按词典序排列,并用逗号分隔。
对于2020-06-02,出售的物品是 (Mask),只需返回该物品名。思路:
- 从
Activities表中查询销售日期(sell_date)和产品(product)信息。 - 使用 count
(distinct product)函数计算每个销售日期下售出的产品的数量,并将结果命名为num_sold。 - 使用 group
_concat(distinct product order by product asc separator ',')函数将每个销售日期下售出的产品按照产品名字升序排列,并以逗号分隔合并成一个字段,命名为products。 - 使用 group
by sell_date将结果按照销售日期分组。 - 使用 order
by sell_date将结果按照销售日期进行升序排序。
group_concat 是一种用于将查询结果集中的多行合并成单行的函数,通常用于将多行数据合并成一行展示。它可以用在 SELECT 查询中,在 GROUP BY 子句的聚合函数中使用。
下面是一个示例用法:
SELECT
department_id,
GROUP_CONCAT(employee_name ORDER BY hire_date SEPARATOR ', ') AS employees
FROM
employees
GROUP BY
department_id; 在上面的例子中,假设 employees 表包含了部门ID和雇员名字等信息,通过使用 group_concat 函数按照部门ID分组,将每个部门的雇员名字合并成一行,并按照入职日期排序以逗号分隔显示
代码:
select sell_date,count(distinct product) as num_sold,
group_concat(distinct product order by product asc separator ',')
as products
from Activities
group by sell_date
order by sell_date