【查找算法】之二分查找

news2024/9/22 17:31:57

一、算法介绍

二分查找，也称为折半查找，是一种在有序数组中查找特定元素的高效算法。对于包含 n 个元素的有序数组，二分查找的步骤如下：

确定搜索范围：首先，将要查找的元素与数组中间的元素进行比较。如果查找的元素等于中间元素，则找到了目标值。否则，如果目标值小于中间元素，则在左半边继续查找；如果目标值大于中间元素，则在右半边继续查找。
缩小搜索范围：根据比较结果，将搜索范围缩小为剩余数组的一半，并重复执行步骤 1，直到找到目标值或确定目标值不存在。

二分查找算法的关键优势在于每一步都能将搜索范围减半，这使得算法的时间复杂度为 O(log n)，相比线性搜索算法的 O(n) 更加高效，尤其是对于大型数据集。

二、时间复杂度计算

二分搜索最坏的情况就是折半一直找到最后一个元素，首先观察规律

开始时，是从n个元素中查找

第一次折半时，是从 $\frac{n}{2}$ 个元素中查找

第二次折半时，是从 $\frac{n}{4}$ 个元素中查找

。

假设第k次折半后只剩一个元素，即是从 $\frac{n}{2^k}$ 个元素中查找

即 $\frac{n}{2^k}$ = 1，即 n = $2^k$ ，由对数定义知道 k = $log_{2}n$ ，在计算机科学中如果没有特殊说明，默认就是以2为底，即k= $\log n$

即操作k次才能找到最后一个元素，所以时间复杂度为O( $\log n$ )

三、Java代码示例

package com.datastructures;

/**
 * 二分查找算法
 * @author hulei
 */
public class BinarySearchExample {
    /**
     * 在有序的整型数组中使用二分查找算法来寻找指定目标值的索引。
     * @param arr 一个已排序的整型数组。
     * @param target 要在数组中查找的目标值。
     * @return 如果目标值存在于数组中，则返回其索引；如果目标值不存在，则返回-1。
     */
    public static int binarySearch(Integer[] arr, int target) {
        int left = 0; // 初始化左边界为数组的第一个元素的索引
        int right = arr.length - 1; // 初始化右边界为数组的最后一个元素的索引

        while (left <= right) { // 当左边界不大于右边界时继续循环
            int mid = left + (right - left) / 2; // 计算中间位置，避免溢出
            if (arr[mid] == target) {
                return mid; // 如果中间位置的元素等于目标值，返回其索引
            } else if (arr[mid] < target) {
                left = mid + 1; // 如果中间位置的元素小于目标值，调整左边界
            } else {
                right = mid - 1; // 如果中间位置的元素大于目标值，调整右边界
            }
        }

        return -1; // 如果没有找到目标值，返回-1
    }

    /**
     * 递归实现的二分查找。
     *
     * @param arr 有序整型数组，查找范围在此数组内。
     * @param target 目标值，我们要在数组中找到这个值的索引。
     * @param left 查找范围的左边界。
     * @param right 查找范围的右边界。
     * @return 如果找到目标值，返回其索引；如果未找到，返回-1。
     */
    public static int binarySearchRecursive(Integer[] arr, int target, int left, int right) {
        // 当左边界大于右边界时，说明已经搜索完毕但未找到目标值，返回-1
        if (left > right) {
            return -1;
        }
        // 计算中间位置，避免直接计算(left + right) / 2可能的溢出问题
        int mid = left + (right - left) / 2;

        // 如果中间位置的元素等于目标值，返回其索引
        if (arr[mid] == target) {
            return mid;
            // 如果中间位置的元素小于目标值，说明目标值可能在中间位置的右边，递归搜索右半部分
        } else if (arr[mid] < target) {
            return binarySearchRecursive(arr, target, mid + 1, right);
            // 如果中间位置的元素大于目标值，说明目标值可能在中间位置的左边，递归搜索左半部分
        } else {
            return binarySearchRecursive(arr, target, left, mid - 1);
        }
    }

    public static void main(String[] args) {
        Integer[] sortedArray = {11, 22, 33, 44, 55, 66, 77, 88, 99, 100, 111, 123};
        int targetValue = 111;
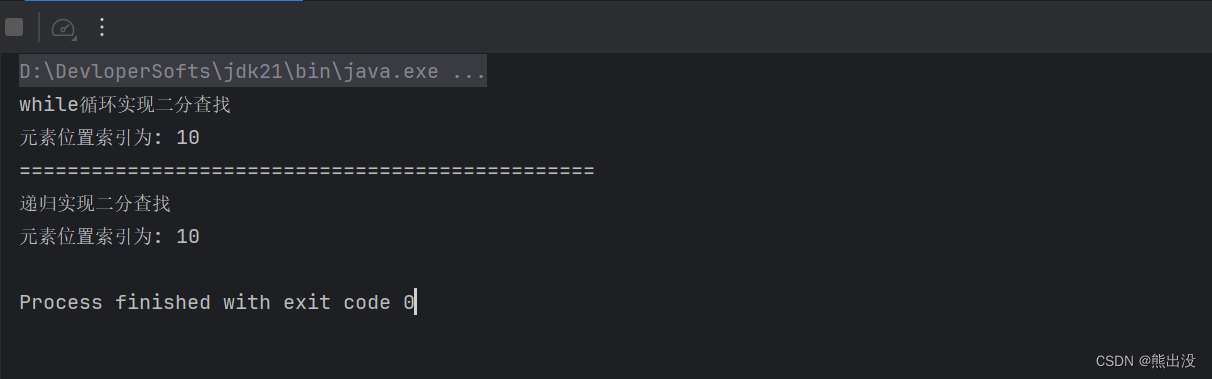
        System.out.println("while循环实现二分查找");
        int resultWithoutRecursive = binarySearch(sortedArray, targetValue);
        if (resultWithoutRecursive != -1) {
            System.out.println("元素位置索引为: " + resultWithoutRecursive);
        } else {
            System.out.println("没有发现目标元素");
        }
        System.out.println("================================================");
        System.out.println("递归实现二分查找");
        int resultRecursive = binarySearchRecursive(sortedArray, targetValue, 0, sortedArray.length - 1);
        if (resultRecursive != -1) {
            System.out.println("元素位置索引为: " + resultRecursive);
        } else {
            System.out.println("没有发现目标元素");
        }

    }
}

代码分析：
该Java函数包含在一个名为BinarySearchExample的类中，提供了两种实现二分查找算法的方法：binarySearch和binarySearchRecursive。二分查找算法用于在有序数组中查找指定目标值的索引。

1. binarySearch方法：

参数：一个已排序的整型数组arr和要查找的目标值target。
返回值：如果目标值存在于数组中，则返回其索引；如果目标值不存在，则返回-1。
实现方式：使用循环迭代来缩小查找范围，直到找到目标值或确定目标值不存在。初始化左边界left为数组的第一个元素的索引，右边界right为数组的最后一个元素的索引。在每次循环中，计算中间位置mid，并将mid与目标值比较，根据比较结果调整左右边界的值。

2. binarySearchRecursive方法：

参数：一个已排序的整型数组arr，要查找的目标值target，以及查找范围的左边界left和右边界right。
返回值：如果目标值存在于数组中，则返回其索引；如果目标值不存在，则返回-1。
实现方式：使用递归来实现二分查找。通过不断缩小查找范围来查找目标值。计算中间位置mid，并将mid与目标值比较，根据比较结果递归调用函数自身，传入更新后的左右边界。
在main方法中，示例代码演示了如何使用这两种方法在有序数组中查找目标值，并输出查找结果。

比如我要在以下数组 Integer[] sortedArray = {11, 22, 33, 44, 55, 66, 77, 88, 99, 100, 111, 123}
中查找目标值为55的元素的索引位置，返回结果为4，即元素55的索引位置为4
在这里插入图片描述