文章考虑了具有订购成本（由单位成本加上重新订购成本组成）的动态库存问题。具体而言，对于每个时期，系统在中期开始是做出一系列采购决策——这些采购有助于库存的积累，并在随后的周期被需求所消耗。每时期系统会产生各种成本，一般包括：采购或订购成本$c(z)$，其中$z$是购买量；持有成本$h(\cdot )$，为时期末供应量超过需求量的函数；以及缺货成本$p(\cdot )$，为周期末需求量超过供应量的函数。每个时期结束时会计算持有成本或缺货成本，而订购成本则在进行采购时计算。库存问题的目标便是选择采购决策以最小化所有成本的折现值的期望。文章在最初假设采购仅在周期开始时进行，并且交货是即时的；后续将假设拓展考虑延迟交货的情况。

设交货后的库存水平立即为$y$，则该周期内将收取的预期持有和缺货成本为$L(y)$:

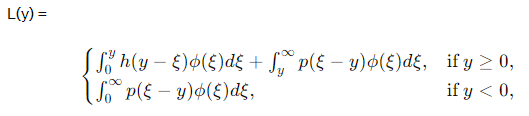
其中$\phi$是需求分布的密度函数。若考虑$n$个时期、初始库存为$x$的库存问题，令$C_n(x)$表示在最优配给下$n$个时期计划的折现成本的期望值（折现因子$\alpha \in [0,1]$）。则可得出$C_n(x)$：
C n ( x ) = min ⁡ y ≥ x { c ( y − x ) + L ( y ) + α ∫ 0 ∞ C n − 1 ( y − ξ ) φ ( ξ ) d ξ } , C_n(x)=\min_{y\geq x}\{c(y-x)+L(y)+\alpha\int_0^{\infty}C_{n-1}(y-\xi)\varphi(\xi)\mathrm{d}\xi\}, Cn​(x)=y≥xmin​{c(y−x)+L(y)+α∫0∞​Cn−1​(y−ξ)φ(ξ)dξ},
如果$y_n(x)$为最优解，则$y_n(x)-x$表示最优的初始购买量。

文章证明，如果持有成本和缺货成本是线性的，则每个时期中的最优策略总是 (s, S) 类型。

首先回顾单时期问题，即$n=1$且$C_0\equiv 0$, 而单时期问题本质上是一个微积分问题。

• 最简单的情况是订购成本是线性的，即$c(z)=c\cdot z$. 在这种情况下，单时期模型的最优策略通常由单个临界数$\bar{x}$定义如下：如果$x<\bar{x}$，则购买$\bar{x}-x$；如果$x>\bar{x}$，则不购买。在多时期问题中，类似的结果通常成立，最优策略由一系列临界数${\bar{x}}_1,{\bar{x}}_2,\cdots$定义。这些结果成立的充分条件是$L(y)$是凸的，而这一条件在持有和短缺成本均为原点处消失的凸递增函数时成立。
• 当订购成本不再是线性时，文章集中讨论了最简单类型的非线性成本：

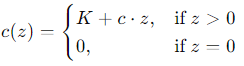
其中$K$通常被描述为固定订购成本。在该订购成本下，单时期模型中的最优策略通常由一对临界数 (s, S) 定义：如果$ x<s $，则订购 $(S-x)$；如果$ x>s $，则不订购。在单时期模型中有一些示例显示这样的策略并非最优。然而，如果持有和短缺成本为线性函数$h(u)=h\cdot u$和$p(u)=p\cdot u$,或者更一般地，如果$L(y)$是凸的，那么多时期模型的最优策略是 (s, S).

然而，即使假设持有和短缺成本是线性的，在原文章发表的60年代前，关于动态模型最优策略的文献也非常少。Bratten
表示（引用章节9），如果需求的密度是递减的，动态模型的最优策略是由一系列临界数对 ($s_1,S_1$), ($s_2,S_2$),… 定义。唯一的另一种结果由 Karlin提出，即如果$\phi$有一个单调似然比，当持有和缺货成本是线性的，且$c+h>\alpha p$，那么最优策略也是同样的类型。这两个结果都相当限制性，前者要求一个递减的密度，后者对成本有严格的约束。

而文章证明了，如果持有成本和缺货成本是线性的，或更一般地，当$L(y)$是凸的并且订购成本如上非线性时，则每个时期中的最优策略总是 (s, S) 类型，无需任何附加条件。

上述两个结果的推导基于对函数$G_n(y)$的研究，其中
$$G_n(y)=cy+L(y)+\alpha {\int }_0^{\infty }{C}_{n-1}(y-\xi )\phi (\xi )\mathrm{d}\xi ,$$
当且仅当 存在$y>x$, $G_n(x)>K+G_n(y)$, 从$x$订购是最优的；若要求从$x$订购，则订购到 使$G_n(y)$最小的$y$$(y>x)$. 当假设 Bratten 的条件或 Karlin 的条件时，$G_n(y)$递减到一个最小值然后再递增。现将最小满足情况的$y$记作$S_n$且定义$s_n$:
$$G_n(s_n)=G_n(S_n)+K,$$
则由 ($s_n,S_n$) 定义的策略是最优的。然而，少量的数值计算就足以显示函数$G_n$并不总是符合次规律——实际上，可能有许多极大值和极小值。文章给出的证明思路是，尽管$G_n$可能有很多极大值和极小值，但其变化不会致使导致偏离 (s,S) 策略。

如果$L(y)$是凸的，对于任一$a\ge 0$, 则$K+G_n(a+x)-G_n(x)-a{G}_n^{\prime }(x)\ge 0$.

文章分情况讨论了即时与延时交货的情况来证明上述不等式的成立。假设$G_n(x)$的变化如图1所示：系统会在区间 I 订购到点$S$，在区间 II 不订购，在区间 III 订购到$S$，在区间 IV 不订购，在区间 V 订购到$S^{\prime }$，在区间 VI 不订购。但若以上不等式成立，则该曲线不能成立：若有让$x+a=S$并且$x$是在 III 中达到相对最大值的点，而对于这个值的$x$, $G_n^{\prime }=0$并且以上不等式意味着 $K+G_n(x)-G_n(x)\ge 0$，这与图1矛盾。同样的论证可以应用于点$S^{\prime }$. 接下来针对订购货物到达的时间分情况讨论。

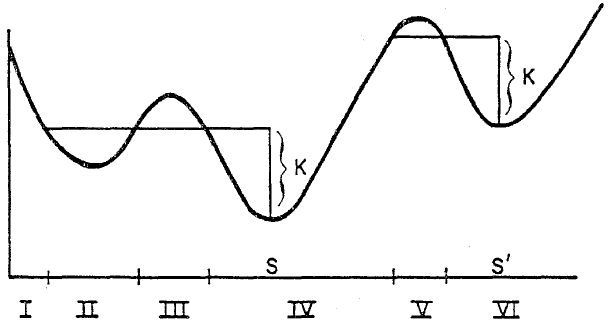
图1. 在假设的订购方案下的期望成本变化

零交货延迟的情况

对于即时交货的情况，文章提出以下定义：

设$K\ge 0$并且$f(x)$是一个可微分函数。如果对于所有$a>0$和所有$x$，有
$$K+f(a+x)-f(x)-a{f}^{\prime }(x)\ge 0,$$
则称$f(x)$是 K-凸的。如果不假设可微分性，则 K-凸性的定义为
$$K+f(a+x)-f(x)-a[\frac{f(x+b)-f(x)}{b}]\ge 0.$$
K-凸函数的简单属性包括：

1. 0-凸性等同于普通凸性。
2. 如果$f(x)$是 K-凸的，那么对于所有$h$,$f(x+h)$也是 K-凸的。
3. 如果$f$和$g$分别是 K-凸和 M-凸的，且有$\alpha$ 和$\beta$为正，那么$\alpha f+\beta g$是$(\alpha K+\beta M)$-凸的。

运用数学归纳法，首先，$G_1(x)=cx+L(x)$显然是 K-凸的（0-凸）。

其次，假设$G_2,\dots ,G_n$也是 K-凸的。根据$G_n(x)$的定义，为证明$G_{n+1}(x)$的 K-凸性，则只需证明${\int }_0^{\infty }{C}_n(x-\xi )\phi (\xi )\mathrm{d}\xi$是 K-凸的，而通过上述属性2和3，足够证明$C_n(x)$是 K-凸的，推导如下。

首先，如果$S_n$是$G_n(x)$的绝对最小值，并且已定义$s_n$为满足$K+G_n(S_n)=G_n(s_n)$的$ x<S_n $，那么最优策略是：当$ x<s_n $则订购到$S_n$，否则不订购。因此，

• 当$ x<s_n $时，$C_n(x)=K+c(S_n-x)+C_n(S_n)=K-cx+G_n(S_n)$;
• 当$ x>s_n $时，$C_n(x) = -cx+G_n(x)$.

情况 1：$x>s_n$. 在这个区域，$C_n(x)$等于线性函数加上K-凸函数，因此是 K-凸的。

情况 2：$ x<s_n<x+a $. 在这种情况下，
$$K+C_n(x+a)-C_n(x)-a{C}_n^{\prime }(x)=K+C_n(x+a)-C_n(x)+ac$$
为正，因为
C n ( x ) = min ⁡ y > x { K + c ( y − x ) + L ( y ) + α ∫ 0 ∞ C n − 1 ( y − ξ ) φ ( ξ ) d ξ } C_n(x)=\min_{y>x}\{K+c(y-x)+L(y)+\alpha\int_0^{\infty}C_{n-1}(y-\xi)\varphi(\xi)\mathrm{d}\xi\} Cn​(x)=y>xmin​{K+c(y−x)+L(y)+α∫0∞​Cn−1​(y−ξ)φ(ξ)dξ}
$$\le K+ca+K(x+a)+\alpha {\int }_0^{\infty }{C}_{n-1}(x+a-\xi )\phi (\xi )\mathrm{d}\xi$$
$$=K+ca+C_n(x+a).$$
情况 3：$ x + a < s_n $.在这个区域，$ C_n(x) $是线性的，因此是 K-凸的。归纳完成，并证明了在这一部分考虑的情况下 (s, S) 策略的最优性。

交货延迟的情况

当存在交货延迟时，最优策略的性质很大程度上取决于是超额需求被积压还是被加急处理。如果超额需求被积压，那么已知最优策略是现有库存加上已订购但尚未交付的库存的函数；如果超额需求被加急处理，最优策略则将复杂得多——文章仅考虑积压为满足需求的情况。

令交货延迟记作$\lambda$，即在时期开始时下的订单在$\lambda$个时期后的开始时交付。考虑$n$个时期，令$x$表示当前库存，$x_1$表示下个时期开始时要交付的库存，$x_j$表示$j$个时期后交付的库存，其中$j=1,2,\dots ,\lambda -1$. 令 $C_n(x,x_1,\dots ,x_{\lambda -1})$表示最小期望成本，则
C n ( x , x 1 , … , x λ − 1 ) = min ⁡ z ≥ 0 { c ( z ) + L ( x ) + α ∫ − ∞ C n − 1 ( x + x 1 − ξ , x 2 , … , z ) φ ( ξ ) d ξ } . C_n(x,x_1,\ldots,x_{\lambda-1})=\min_{z\geq 0}\{c(z)+L(x)+\alpha\int_-^{\infty}C_{n-1}(x+x_1-\xi,x_2,\ldots,z)\varphi(\xi)\mathrm{d}\xi\}. Cn​(x,x1​,…,xλ−1​)=z≥0min​{c(z)+L(x)+α∫−∞​Cn−1​(x+x1​−ξ,x2​,…,z)φ(ξ)dξ}.
接下来将证明，如$L(x)$是凸的，并且购买成本如前文所示非线性，最优策略可由$S_n$和$s_n$描述：如果$ x+x_1+\ldots +x_{\lambda-1}>s_n $则不订购；如果$ x+x_1+\ldots +x_{\lambda-1}<s_n $则订购到$S_n$.

根据$C_n(x,x_1,\dots ,x_{\lambda -1})$定义，对于$n\ge \lambda$：
$$C_n(x,x_1,x_2,\dots ,x_{\lambda -1})$$
$$=L(x)+\alpha {\int }_0^{\infty }L(x+x_1-\xi )\phi (\xi )\mathrm{d}\xi +\cdots$$
$$+{\alpha }^{\lambda -1}{\int }_0^{\infty }\cdots {\int }_0^{\infty }L(x+\cdots +x_{\lambda -1}-\sum _{i=1}^{\lambda -1}{\xi }_i)\phi ({\xi }_1)\cdots \phi ({\xi }_{\lambda -1})\mathrm{d}\xi \cdots \mathrm{d}{\xi }_{\lambda -1}+f_n(x+x_1+\cdots +x_{\lambda -1}),$$
其中$f_n(u)$满足
f n ( u ) = min ⁡ x ≥ 0 { c ( z ) + α λ ∫ 0 ∞ ⋯ ∫ 0 ∞ L ( u + z − ∑ i = 1 λ ξ i ) φ ( ξ 1 ) ⋯ φ ( ξ λ ) d ξ 1 ⋯ d ξ λ } . f_n(u)=\min_{x\geq0}\{c(z)+\alpha^{\lambda}\int_0^{\infty}\cdots\int_0^{\infty}L(u+z-\sum_{i=1}^{\lambda}\xi_i)\varphi(\xi_1)\cdots\varphi(\xi_{\lambda})\mathrm{d}\xi_1\cdots\mathrm{d}\xi_{\lambda}\}. fn​(u)=x≥0min​{c(z)+αλ∫0∞​⋯∫0∞​L(u+z−i=1∑λ​ξi​)φ(ξ1​)⋯φ(ξλ​)dξ1​⋯dξλ​}.
因此若令$y=u+z$，即相当于$L(y)$被
$${\alpha }^{\lambda }{\int }_0^{\infty }\cdots {\int }_0^{\infty }L(u+z-\sum _{i=1}^{\lambda }{\xi }_i)\phi ({\xi }_1)\cdots \phi ({\xi }_{\lambda })\mathrm{d}{\xi }_1\cdots \mathrm{d}{\xi }_{\lambda }\}$$
替换。然而，如果$L(y)$是凸的，那么替换它的上式也是凸的，这就足以完成证明。于是可以得出结论，如果持有成本和缺货成本是线性的，则每个时期中的最优策略总是 (s, S) 类型。

参考文献​

​
ARROW, K. J., T. HARRIS, and J. MARSCHAK. “Optimal Inventory Policy,” Econometrica, 19(1951), 250-72.​

ARROW, K. J., S. KARLIN, and H. SCARF. Studies in the Mathematical Theory of Inventory and Production, Stanford, Calif.: Stanford University Press, 1958.​

BELLMAN, R., I. GLICKSBERG, and O. GROSS. “On the Optimal Inventory Equation,” Management Science, 2(1955), 83-104.​

DVORETZKY, A., J. KIEFER, and J. WOLFOWITZ. “The Inventory Problem, I. Case of Known Distributions of Demand,” Econometrica, 20(1952), 187-222.​

DVORETZKY, A., J. KIEFER, and J. WOLFOWITZ. “On the Optimal Character of the (S,s) Policy in Inventory Theory,” Econometrica, 21(1953), 586-96.