二.数据结构

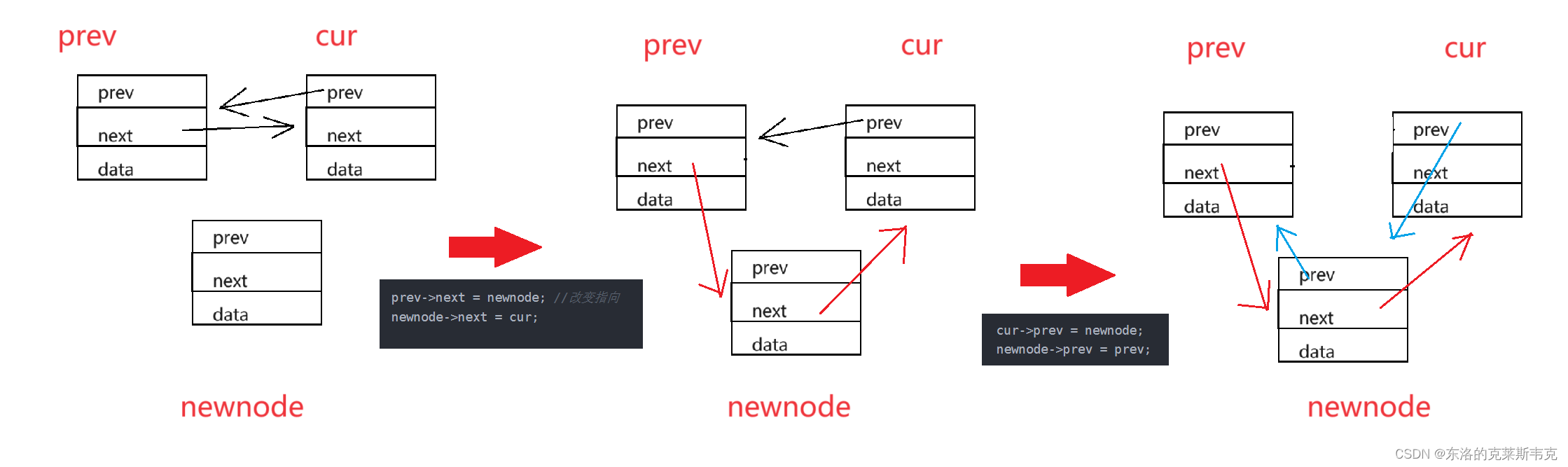
单链表

数组实现单链表:
int head;    //head存储这个单链表的头结点
int value[N];//value存储结点的值
int nextt[N];//nextt存储结点的next指针
int id;      //id表示当前用到的点的位置
//初始化:
void Init(){
    head=-1,id=0;//链表的头节点要指向-1,当前结点位置为0
}
//在单链表表头处插入一个数x:
void Head_Insert_x(int x){
    value[id]=x;   //存储x的数据
    nextt[id]=head;//存储x的指针,指向头结点
    head=id++;     //更新head后移动id指针
}
//删除第k个插入的数后面的数:
void Delete_k(int k){
    nextt[k]=nextt[nextt[k]];//让k的指针指向k下一个的下一个
    //删除头结点:head=nextt[head];
}
//在第k个插入的数后面插入一个数x:
void Insert_k_x(int k,int x){
    value[id]=x;       //存储x的数据
    nextt[id]=nextt[k];//存储x的指针,指向k指向next
    nextt[k]=id++;     //更新k的指针后移动id指针
}
//遍历单链表:
for(int i=head;i!=-1;i=nextt[i])
    cout<<value[i]<<" ";

双链表

数组实现双链表:
int value[N],l[N],r[N],id;
//初始化:
void Init(){
    r[0]=1,l[1]=0;//0表示左端点,1表示右端点
    id=2;         //0和1已经被占用
}
//将第k个点删除
void Delete(int k){
    r[l[k]]=r[k];
    l[r[k]]=l[k];
}
//在第k个点右侧插入一个数x:
void Insert_R(int k,int x){
    value[id]=x;
    r[id]=r[k];
    l[id]=k;
    l[r[k]]=id;
    r[k]=id;
    id++;
}
//在第k个点左侧插入一个数x:
void Insert_L(int k,int x){
    value[id]=x;
    l[id]=l[k];
    r[id]=k;
    r[l[k]]=id;
    l[k]=id;
    id++;
}
//遍历双链表:
for(int i=r[0];i!=1;i=r[i])
    cout<<value[i]<<" ";

栈

数组实现栈:
int stackk[N];//栈数组
int ttop;     //栈顶指针
//初始化栈
void Stack_Init(){
    memset(stackk,0,sizeof(stackk));
    ttop=0;
}
//入栈
void Stack_Push(int x){
    stackk[++ttop]=x;
}
//出栈
void Stack_Pop(){
    ttop--;
}
//查询栈顶元素
int Stack_Top(){
    return stackk[ttop];
}
//判空
bool Stack_Empty(){
    if(ttop>0) return false;
    else return true;
}

单调栈

//当栈顶元素大于当前待入栈元素时,出栈
while(!Stack_Empty()&&Stack_Top()>=x) Stack_Pop();
//再把带入栈元素入栈
Stack_Push(x);

队列

数组实现队列:
int queue[N],head,tail=-1;
//初始化队列
void Queue_Init(){
    memset(queue,0,sizeof(queue));
    head=0,tail=-1;
}
//入队
void Queue_Push(int x){
    queue[++tail]=x;
}
//队头出队
void Queue_Pop_head(){
    head++;
}
//队尾出队
void Queue_Pop_tail(){
    tail--;
}
//查询队头
int Queue_Head(){
   return queue[head]; 
}
//查询队尾
int Queue_Tail(){
   return queue[tail]; 
}
//判空
bool Queue_Empty(){
    if(head<=tail) return false;
    else return true;
}

单调队列

数组a[]:1,2,3,...,n
单调增队列--找最小值:
//当新进入窗口的值小于队尾元素时,队尾出队
while(!Queue_Empty()&&Queue_Tail()>a[i]) Queue_Pop_tail();
//将新进入窗口的元素入队
Queue_Push(a[i]);
//如果队头滑出了窗口,则队头出队
if(i-k>=1&&Queue_Head()==a[i-k]) Queue_Pop_head();
//如果窗口形成,则输出队头
if(i>=k) cout<<Queue_Head()<<" ";

单调减队列--找最大值:
while(!Queue_Empty()&&Queue_Tail()<a[i]) Queue_Pop_tail();
Queue_Push(a[i]);
if(i-k>=1&&Queue_Head()==a[i-k]) Queue_Pop_head();
if(i>=k) cout<<Queue_Head()<<" ";

KMP

//初始化
int n,m,nextt[N];
//nextt[j]表示短串(1到j)的前缀和后缀相同的最大长度
char p[N],s[N];//长串为s长度为n,短串为p长度为m
//求nextt的过程:遍历p
for(int i=2,j=0;i<=m;i++){
    //当j有对应p串的元素,且p[i]!=p[j+1],则匹配失败,需要移动p串,直到匹配或整个p串移到后面
    while(j&&p[i]!=p[j+1]) j=nextt[j];
    //如果当前元素匹配,j后移一位
    if(p[i]==p[j+1]) j++;
    //给nextt赋值
    nextt[i]=j;
}
//KMP匹配过程:遍历s
for(int i=1,j=0;i<=n;i++){
    //当j有对应p串的元素,且s[i]!=p[j+1],则匹配失败,需要移动p串,直到匹配或整个p串移到后面
    while(j&&s[i]!=p[j+1]) j=nextt[j];
    //如果当前元素匹配,j后移一位
    if(s[i]==p[j+1]) j++;
    //如果匹配成功
    if(j==m){
        //继续匹配下一个子串
        j=nextt[j];
    }
}

上述代码第一个过程求nextt数组,实际上就是求最长匹配长度的一个过程.

以下练习(www.luogu.com)可以让我们更好的理解和掌握KMP算法:

P3375 【模板】KMP

#include<iostream>
using namespace std;
const int N=1e6+5;
string a,b,a0,b0;
int n,m,nextt[N];
int main(){
    cin>>a0>>b0;
    a="0";a+=a0;
    b="0";b+=b0;
    n=a.size()-1,m=b.size()-1;
    for(int i=2,j=0;i<=m;i++){
        while(j&&b[i]!=b[j+1]) j=nextt[j];
        if(b[i]==b[j+1]) j++;
        nextt[i]=j;
    }
    for(int i=1,j=0;i<=n;i++){
        while(j&&a[i]!=b[j+1]) j=nextt[j];
        if(a[i]==b[j+1]) j++;
        if(j==m){
            cout<<i-m+1<<endl;
            j=nextt[j];
        }
    }
    for(int i=1;i<=m;i++) cout<<nextt[i]<<" ";
    return 0;
}

P4391 [BOI2009] Radio Transmission 无线传输

#include<iostream>
using namespace std;
const int N=1e6+5;
int n,nextt[N];
char s[N];
int main(){
    cin>>n>>s+1;
    if(n==1){
        cout<<1<<endl;
        return 0;
    }
    for(int i=2,j=0;i<=n;i++){
        while(j&&s[i]!=s[j+1]) j=nextt[j];
        if(s[i]==s[j+1]) j++;
        nextt[i]=j;
    }
    cout<<n-nextt[n]<<endl;
    return 0;
}

P3435 [POI2006] OKR-Periods of Words

#include<iostream>
using namespace std;
const int N=1e6+5;
int n,nextt[N];
long long ans;
char s[N];
int main(){
    cin>>n>>s+1;
    //KMP求最长匹配长度
    for(int i=2,j=0;i<=n;i++){
        while(j&&s[i]!=s[j+1]) j=nextt[j];
        if(s[i]==s[j+1]) j++;
        nextt[i]=j;
    }
    //遍历求最短匹配长度
    for(int i=2,j=0;i<=n;i++){
        //i,j相等
        j=i;
        //递推求最小长度
        while(nextt[j]) j=nextt[j];
        //记忆化
        if(nextt[i]) nextt[i]=j;
        //计数
        ans+=i-j;
    }
    cout<<ans<<endl;
    return 0;
}

P2375 [NOI2014] 动物园

#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=1e6+5;
const int mod=1e9+7;
int m,n,nextt[N],num[N];
int main(){
    cin>>m;
    while(m--){
        ll ans=1;num[1]=1;
        string s="0",s0;
        cin>>s0;
        s+=s0;
        n=s.size()-1;
        for(int i=2,j=0;i<=n;i++){
            while(j&&s[i]!=s[j+1]) j=nextt[j];
            if(s[i]==s[j+1]) j++;
            nextt[i]=j;
            num[i]=num[j]+1;
        }
        for(int i=2,j=0;i<=n;i++){
            while(j&&s[i]!=s[j+1]) j=nextt[j];
            if(s[i]==s[j+1]) j++;
            while(j>i/2) j=nextt[j];
            ans=(ans*(ll)(num[j]+1))%mod;
        }
        cout<<ans<<endl;
    }
    return 0;
}

Trie

Trie树:高效地存储和查找字符串集合的数据结构
//son[][]存储子节点的位置,分支最多26条；
//cnt[]存储以某节点结尾的字符串个数
//id表示当前要插入的节点是第几个,每创建一个节点值+1
int son[N][26],cnt[N],id;
void Insert(string s){
    int n=s.size();
    int j=0;             //从根结点开始遍历
    for(int i=0;i<n;i++){
        int x=s[i]-'a';
        if(!son[j][x]) son[j][x]=++id;//没有子结点就创建
        j=son[j][x];//j移动到下一个结点位置
    }
    cnt[j]++;//遍历完串后计数
    return ;
}
int Query(string s){
    int n=s.size();
    int j=0;
    for(int i=0;i<n;i++){
        int x=s[i]-'a';
        if(!son[j][x]) return 0;
        j=son[j][x];
    }
    return cnt[j];
}

以下练习可以让我们更好的理解和掌握Trie算法:

AcWing 143. 最大异或对

异或运算 ^ :相同为0,不同为1
如:
    010010
   ^100110
   =110100

暴力法:

#include<iostream>
using namespace std;
const int N=1e5+5;
int n,a[N],ans;
int main(){
    cin>>n;
    for(int i=0;i<n;i++) cin>>a[i];
    for(int i=0;i<n;i++)
        for(int j=0;j<i;j++)
            ans=max(ans,a[i]^a[j]);
    cout<<ans<<endl;
    return 0;
}

Trie优化:

#include<iostream>
using namespace std;
const int N=1e5+5,M=31*N;
int n,a[N],ans;
int son[M][2],id;
void Inert(int num){
    int j=0;
    for(int i=30;i>=0;i--){
        int x=num>>i&1;//num的第i位的二进制数是什么
        if(!son[j][x]) son[j][x]=++id;//如果插入中发现没有该子节点,则创建一个
        j=son[j][x];   //指针指向下一层
    }
    return ;
}
int Query(int num){
    int j=0,res=0;
    for(int i=30;i>=0;i--){//从最大位开始遍历
        int x=num>>i&1;
        if(son[j][!x]){   //如果存在好的结点可以选择
            res=res*2+!x; //更新res:*2相当于整体向左移一位,然后加上末位
            j=son[j][!x]; //移动指针
        }
        else{             //否则只能选当前存在的结点
            res=res*2+x;
            j=son[j][x];
        }
    }
    return res;
}
int main(){
    cin>>n;
    for(int i=0;i<n;i++) cin>>a[i];
    for(int i=0;i<n;i++){   //边插边找
        Inert(a[i]);        //插入当前数
        int t=Query(a[i]);  //查找与当前数异或最大的数
        ans=max(ans,a[i]^t);//更新ans
    }
    cout<<ans<<endl;
    return 0;
}

P2580 于是他错误的点名开始了

#include<iostream>
#include<cstring>
using namespace std;
const int N=5e5+5;
int son[N][26],cnt[N],id;
void Insert(string s){
    int n=s.size();
    int j=0;
    for(int i=0;i<n;i++){
        int x=s[i]-'a';
        if(!son[j][x]) son[j][x]=++id;
        j=son[j][x];
    }
    cnt[j]++;
    return ;
}
int Query(string s){
    int n=s.size();
    int j=0;
    for(int i=0;i<n;i++){
        int x=s[i]-'a';
        if(!son[j][x]) return 0;
        j=son[j][x];
    }
    return cnt[j];
}
void Delete(string s){
    int n=s.size();
    int j=0;
    for(int i=0;i<n;i++){
        int x=s[i]-'a';
        j=son[j][x];
    }
    cnt[j]=1e9;
    return ;
}
int main(){
    int n,m;
    cin>>n;
    while(n--){
        string s;
        cin>>s;
        Insert(s);
    }
    cin>>m;
    while(m--){
        string s;
        cin>>s;
        if(Query(s)==1e9) cout<<"REPEAT"<<endl;
        else if(Query(s)==0) cout<<"WRONG"<<endl;
        else {cout<<"OK"<<endl;Delete(s);}
    }
    return 0;
}

P8306 【模板】字典树

#include<iostream>
#include<cstring>
using namespace std;
const int N=3e6+5;
int son[N][62],cnt[N],id;
//(48)0..9(57) (97)a..z(122) (65)A..Z(90)
void Init_Trie(int x){
    for(int i=0;i<=x;i++){
        cnt[i]=0;
        for(int j=0;j<62;j++){
            son[i][j]=0;
        }
    }
    return ;
}
void Insert_ALL(string s){
    int n=s.size();
    int j=0;
    for(int i=0;i<n;i++){
        int x=s[i];
        if(x>=48&&x<=57) x-=48;
        if(x>=97&&x<=122) x-=87;
        if(x>=65&&x<=90) x-=29;
        if(!son[j][x]) son[j][x]=++id;
        j=son[j][x];
        cnt[j]++; //每一次都要计数
    }
    return ;
}
int Query(string s){
    int n=s.size();
    int j=0;
    for(int i=0;i<n;i++){
        int x=s[i];
        if(x>=48&&x<=57) x-=48;
        if(x>=97&&x<=122) x-=87;
        if(x>=65&&x<=90) x-=29;
        if(!son[j][x]) return 0;
        j=son[j][x];
    }
    return cnt[j];
}
int main(){
    ios::sync_with_stdio(false);
    int T;
    cin>>T;
    while(T--){
        Init_Trie(id);
        id=0;
        int n,m;
        cin>>n>>m;
        while(n--){
            string s;
            cin>>s;
            Insert_ALL(s);
        }
        while(m--){
            string s;
            cin>>s;
            cout<<Query(s)<<endl;
        }
    }
    return 0;
}

P5149 会议座位

#include<iostream>
#include<cstring>
using namespace std;
const int N=5e5+5;
typedef long long ll;
int son[N][52],cnt[N],id;
int num[N],temp[N];
ll ans;
//(97)a..z(122) (65)A..Z(90)
void Init_Trie(int x){
    for(int i=0;i<=x;i++){
        cnt[i]=0;
        for(int j=0;j<62;j++){
            son[i][j]=0;
        }
    }
    id=0;
    return ;
}
void Insert(string s,int flag){
    int n=s.size();
    int j=0;
    for(int i=0;i<n;i++){
        int x=s[i];
        if(x>=97&&x<=122) x-=97;
        if(x>=65&&x<=90) x-=39;
        if(!son[j][x]) son[j][x]=++id;
        j=son[j][x];
    }
    cnt[j]=flag;
    return ;
}
void Query(string s,int flag){
    int n=s.size();
    int j=0;
    for(int i=0;i<n;i++){
        int x=s[i];
        if(x>=97&&x<=122) x-=97;
        if(x>=65&&x<=90) x-=39;
        if(!son[j][x]) return ;
        j=son[j][x];
    }
    num[flag]=cnt[j];
    return ;
}
void mergesort(int l,int r){
    if(l>=r) return ;
    int mid=(l+r)/2;
    mergesort(l,mid);
    mergesort(mid+1,r);
    int i=l,j=mid+1,k=0;
    while(i<=mid&&j<=r){
        if(num[i]<=num[j]) temp[k++]=num[i++];
        else temp[k++]=num[j++],ans+=mid-i+1;
    }
    while(i<=mid) temp[k++]=num[i++];
    while(j<=r) temp[k++]=num[j++];
    for(int i=l,j=0;i<=r;i++,j++) num[i]=temp[j];
    return ;
}
int main(){
    ios::sync_with_stdio(false);
    int n;
    cin>>n;
    Init_Trie(id);
    for(int i=0;i<n;i++){
        string s;
        cin>>s;
        Insert(s,i);
    }
    for(int i=0;i<n;i++){
        string s;
        cin>>s;
        Query(s,i);
    }
    mergesort(0,n-1);
    cout<<ans<<endl;
    return 0;
}

并查集

并查集:
将两个集合合并
查询两个元素是否在同一个集合之中

int n,dad[N],sizee[N];//sizee数组规定只有祖宗结点是有效值
//初始化所有集合
void Init(){
    for(int i=1;i<=n;i++){
        dad[i]=i;
        sizee[i]=1;
    }
    return ;
}
//查找a的祖宗节点
int Find(int a){
    if(dad[a]!=a) dad[a]=Find(dad[a]);//每个集合中只有祖宗节点的值等于自身的值
    return dad[a];
}
//将a和b的两个数所在的集合合并
void Merge(int a,int b){
    if(Find(a)==Find(b)) return ;//特判a,b本身就在同一个集合之中
    //先更新sizee数组再合并
    sizee[Find(b)]+=sizee[Find(a)];
    dad[Find(a)]=Find(b);
    return ;
}
//判断a,b是否在同一个集合之中
bool Check(int a,int b){
    if(Find(a)==Find(b)) return true;
    else return false;
}
//统计a所在集合的元素个数
int Count(int a){
    return sizee[Find(a)];
}

以下练习可以让我们更好的理解和掌握并查集算法:

P3367 【模板】并查集

#include<iostream>
using namespace std;
const int N=1e5+5;
int n,m,dad[N];
void Init(){
    for(int i=1;i<=n;i++) dad[i]=i;
    return ;
}
int Find(int a){
    if(dad[a]!=a) dad[a]=Find(dad[a]);
    return dad[a];
}
void Merge(int a,int b){
    if(Find(a)!=Find(b)) dad[Find(a)]=Find(b);
    return ;
}
bool Check(int a,int b){
    if(Find(a)==Find(b)) return true;
    else return false;
}
int main(){
    ios::sync_with_stdio(false);
    cin>>n>>m;
    Init();
    while(m--){
        int z,x,y;
        cin>>z>>x>>y;
        if(z==1){
            Merge(x,y);
        }
        if(z==2){
            if(Check(x,y)) puts("Y");
            else puts("N");
        }
    }
    return 0;
}

P2256 一中校运会之百米跑

#include<iostream>
using namespace std;
const int N=2e4+5;
int n,m,dad[N];
struct student{
    int num;
    string name;
}stu[N];
int Trans(string a){
    for(int i=1;i<=n;i++) if(stu[i].name==a) return stu[i].num;
    return 0;
}
void Init(){
    for(int i=1;i<=n;i++) dad[i]=i;
    return ;
}
int Find(int a){
    if(dad[a]!=a) dad[a]=Find(dad[a]);
    return dad[a];
}
void Merge(int a,int b){
    if(Find(a)!=Find(b)) dad[Find(a)]=Find(b);
    return ;
}
bool Query(int a,int b){
    if(Find(a)==Find(b)) return true;
    else return false;
}
int main(){
    cin>>n>>m;
    Init();
    for(int i=1;i<=n;i++){
        cin>>stu[i].name;
        stu[i].num=i;
    }
    while(m--){
        string a,b;
        cin>>a>>b;
        Merge(Trans(a),Trans(b));
    }
    int k;
    cin>>k;
    while(k--){
        string a,b;
        cin>>a>>b;
        int x=Trans(a),y=Trans(b);
        if(x&&y&&Query(x,y)) cout<<"Yes."<<endl;
        else cout<<"No."<<endl;
    }
    return 0;
}

P8654 [蓝桥杯 2017 国 C] 合根植物

#include<iostream>
using namespace std;
const int N=1e6+5;
int n,m,k,dad[N],ans;
void Init(){
    for(int i=1;i<=n*m;i++) dad[i]=i;
    return ;
}
int Find(int a){
    if(dad[a]!=a) dad[a]=Find(dad[a]);
    return dad[a];
}
void Merge(int a,int b){
    if(Find(a)!=Find(b)) dad[Find(a)]=Find(b);
    return ;
}
int main(){
    cin>>m>>n>>k;
    Init();
    while(k--){
        int a,b;
        cin>>a>>b;
        Merge(a,b);
    }
    for(int i=1;i<=n*m;i++) if(dad[i]==i) ans++;
    cout<<ans<<endl;
    return 0;
}

P8403 [CCC2022 J4] Good Groups

P8396 [CCC2022 S2] Good Groups

并查集+暴力(85 points):

#include<iostream>
using namespace std;
const int N=1e5+5;
int n,m,k,dad[3*N],ans;
string flag[3*N];
typedef pair<string,string>pss;
pss must[N],mustnot[N];
int Trans(string a){
    for(int i=1;i<=k*3;i++){
        if(flag[i]==a){
            return i;
        }
    }
    return 0;
}
void Init(){
    for(int i=1;i<=3*k;i++) dad[i]=i;
    return ;
}
int Find(int a){
    if(dad[a]!=a) dad[a]=Find(dad[a]);
    return dad[a];
}
void Merge(int a,int b){
    if(Find(a)!=Find(b)) dad[Find(a)]=Find(b);
    return ;
}
bool Check(int a,int b){
    if(Find(a)==Find(b)) return true;
    else return false;
}
int main(){
    ios::sync_with_stdio(false);
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>must[i].first>>must[i].second;
    }
    cin>>m;
    for(int i=1;i<=m;i++){
        cin>>mustnot[i].first>>mustnot[i].second;
    }
    cin>>k;
    Init();
    for(int i=1;i<=3*k;i+=3){
        cin>>flag[i]>>flag[i+1]>>flag[i+2];
        Merge(i,i+1);
        Merge(i+1,i+2);
    }
    for(int i=1;i<=n;i++){
        string x=must[i].first,y=must[i].second;
        if(!Check(Trans(x),Trans(y))) ans++;
    }
    for(int i=1;i<=m;i++){
        string x=mustnot[i].first,y=mustnot[i].second;
        if(Check(Trans(x),Trans(y))) ans++;
    }
    cout<<ans<<endl;
    return 0;
}

并查集+unordered_map(AC):

#include<iostream>
#include<unordered_map>
using namespace std;
const int N=1e5+5;
int n,m,k,dad[3*N],ans;
unordered_map<string,int>mapp;
typedef pair<string,string>pss;
pss must[N],mustnot[N];
int Trans(string a){
    return mapp[a];
}
void Init(){
    for(int i=1;i<=3*k;i++) dad[i]=i;
    return ;
}
int Find(int a){
    if(dad[a]!=a) dad[a]=Find(dad[a]);
    return dad[a];
}
void Merge(int a,int b){
    if(Find(a)!=Find(b)) dad[Find(a)]=Find(b);
    return ;
}
bool Check(int a,int b){
    if(Find(a)==Find(b)) return true;
    else return false;
}
int main(){
    ios::sync_with_stdio(false);
    cin>>n;
    for(int i=1;i<=n;i++) cin>>must[i].first>>must[i].second;
    cin>>m;
    for(int i=1;i<=m;i++) cin>>mustnot[i].first>>mustnot[i].second;
    cin>>k;
    Init();
    for(int i=1;i<=3*k;i+=3){
        string a,b,c;
        cin>>a>>b>>c;
        mapp.insert({a,i});
        mapp.insert({b,i+1});
        mapp.insert({c,i+2});
        Merge(i,i+1);
        Merge(i+1,i+2);
    }
    for(int i=1;i<=n;i++){
        string x=must[i].first,y=must[i].second;
        if(!Check(Trans(x),Trans(y))) ans++;
    }
    for(int i=1;i<=m;i++){
        string x=mustnot[i].first,y=mustnot[i].second;
        if(Check(Trans(x),Trans(y))) ans++;
    }
    cout<<ans<<endl;
    return 0;
}

P1840 Color the Axis

这题标记一下
#include<iostream>
using namespace std;
const int N=2e5+5;
int n,m,cnt,dad[N];
void Init(){
    for(int i=1;i<=n;i++) dad[i]=i;
    return ;
}
int Find(int a){
    if(dad[a]!=a) dad[a]=Find(dad[a]);
    return dad[a];
}
int main(){
    ios::sync_with_stdio(false);
    cin>>n>>m;
    Init();
    while(m--){
        int a,b;
        cin>>a>>b;
        b=Find(b);
        //固定染色区间的左端点,将整个区间合并(从右向左)
        while(a<=b){
            if(a!=b&&Find(a)==b) break;
            dad[b]=Find(dad[b-1]);
            cnt++;
            b=Find(b);
        }
        cout<<n-cnt<<endl;
    }
    return 0;
}

P8686 [蓝桥杯 2019 省 A] 修改数组

纯暴力混80points:

#include<iostream>
using namespace std;
const int N=1e5+5;
int n,flag[N],a[N];
int main(){
    ios::sync_with_stdio(false);
    cin>>n;
    for(int i=1;i<=n;i++) {
        cin>>a[i];
        if(flag[a[i]]==0) flag[a[i]]++;
        else{
            for(int j=a[i];j<=N;j++){
                if(flag[j]==0){
                    a[i]=j;
                    flag[j]++;
                    break;
                }
            }
        }
    }
    for(int i=1;i<=n;i++) cout<<a[i]<<" ";
    return 0;
}

并查集(AC):

这题标记一下
#include<iostream>
using namespace std;
const int N=1e6+5;
int n,dad[N],a[N];
void Init(){
    for(int i=1;i<N;i++) dad[i]=i;
    return ;
}
int Find(int a){
    if(dad[a]!=a) dad[a]=Find(dad[a]);
    return dad[a];
}
int main(){
    ios::sync_with_stdio(false);
    cin>>n;
    Init();
    for(int i=1;i<=n;i++){
        cin>>a[i];
        a[i]=Find(a[i]);//变为自己的祖先
        cout<<a[i]<<" ";
        dad[a[i]]++;    //祖先的祖先变为不同的数
    }
    return 0;
}

P1551 亲戚

#include<iostream>
using namespace std;
const int N=5e3+5;
int n,m,p,dad[N];
void Init(){
    for(int i=1;i<=n;i++) dad[i]=i;
    return ;
}
int Find(int a){
    if(dad[a]!=a) dad[a]=Find(dad[a]);
    return dad[a];
}
void Merge(int a,int b){
    if(Find(a)!=Find(b)) dad[Find(a)]=Find(b);
    return ;
}
bool Query(int a,int b){
    if(Find(a)==Find(b)) return true;
    else return false;
}
int main(){
    ios::sync_with_stdio(false);
    cin>>n>>m>>p;
    Init();
    while(m--){
        int a,b;
        cin>>a>>b;
        Merge(a,b);
    }
    while(p--){
        int a,b;
        cin>>a>>b;
        if(Query(a,b)) puts("Yes");
        else puts("No");
    }
    return 0;
}

P2024 [NOI2001] 食物链

这题标记一下
#include<iostream>
using namespace std;
const int N=5e4+5,mod=3;
int n,k,ans;
int dad[N],dist[N];//dist存储当前结点到父结点的距离,只有三种:0,1,2
void Init(){
    for(int i=1;i<=n;i++){
        dad[i]=i;
        dist[i]=0;
    }
    return ;
}
int Find(int a){
    if(dad[a]!=a){
        int temp=dad[a];                 //临时存储父亲结点位置
        dad[a]=Find(dad[a]);             //更新dad数组,实现路径压缩
        dist[a]=(dist[a]+dist[temp])%mod;//更新dist数组
    }
    return dad[a];
}
bool Check_Merge(int x,int y){
    int dadx=Find(x),dady=Find(y);
    //如果x和y的父结点在同一个根结点上,只需要判断距离是否相等
    if(dadx==dady) return dist[x]%mod==dist[y]%mod;
    else{//如果x和y的父结点不在同一个根结点上,需要先进行合并
        dad[dadx]=dady;
        //合并的时候,只需要计算dist[dadx],并且满足x和y在同一类上
        //dist[y]%mod==(dist[x]+dist[dadx])%mod
        dist[dadx]=((dist[y]-dist[x])+mod)%mod;
        return true;
    }
}
bool Check_Eat(int x,int y){
    int dadx=Find(x),dady=Find(y);
    //如果x和y的父结点在同一个根结点上,只需要判断是否满足吃的条件
    if(dadx==dady) return dist[x]%mod==(dist[y]+1)%mod;
    else{//如果x和y的父结点不在同一个根结点上,先需要进行合并
        dad[dady]=dadx;
        //合并的时候,只需要计算dist[dady],并且满足吃的条件
        //dist[x]%mod==(dist[y]+dist[dady]+1)%mod
        dist[dady]=((dist[x]-dist[y]-1)+mod)%mod;
        return true;
    }
}
int main(){
    cin>>n>>k;
    Init();
    while(k--){
        int t,x,y;
        cin>>t>>x>>y;
        if(x>n||y>n) ans++;
        else{
            if(t==1&&!Check_Merge(x,y)) ans++;
            if(t==2&&!Check_Eat(x,y)) ans++;
        }
    }
    cout<<ans<<endl;
    return 0;
}

堆

堆
插入一个数       heap[++size]=x; up(size);
求集合中的最小值  heap[1];
删除最小值       heap[1]=heap[size]; size--; down(1);
删除任意一个元素  heap[k]=heap[size]; size--; up(k);down(k);
修改任意一个元素  heap[k]=x; up(k);down(k);
//堆排序
void heap_sort(){
    //从sizee/2开始,把堆初始化成小根堆,把数字大的下沉
    for(int i=sizee/2;i;i--) down(i);
    return ;
}
//查询堆顶元素
int heap_top(){
    return heap[1];
}
//删除堆顶元素
void heap_pop(){
    heap[1]=heap[sizee];
    sizee--;
    down(1);
    return ;
}

//heap[i]表示第i个结点存储的值,2*i是左子节点,2*i+1是右子节点
//sizee既表示堆里存储的元素个数,又表示最后一个结点的下标
//id :已经插入过多少结点
//kp[k] :堆中第k个插入的数——>heap中结编号的映射
//pk[p] :堆中结点编号为p——>heap中第k插入的个数的映射
int heap[N],sizee,id,kp[N],pk[N];
//交换函数
void h_swap(int a,int b){
    swap(heap[a],heap[b]);
    //交换映射
    swap(pk[a],pk[b]);
    swap(kp[pk[a]],kp[pk[b]]);
}
//插入一个数x
void Insert(int x){
    heap[++sizee]=x;
    pk[sizee]=++id;
    kp[id]=sizee;
    up(sizee);
}
//局部下沉函数
void down(int x){
    int t=x;//t存储三个结点中存在并且最小的结点的下标,初始化为当前结点x
    if(2*x<=sizee&&heap[2*x]<heap[t]) t=2*x;//左子节点存在并且小于当前结点,更新t的下标
    if(2*x+1<=sizee&&heap[2*x+1]<heap[t]) t=2*x+1;//右子节点存在并且小于当前结点,更新t的下标
    //如果t==x意味着不用交换,x就是三个结点中拥有最小值的结点下标,否则交换数值并且继续递归
    if(t!=x){
        h_swap(t,x);
        down(t);
    }
    return ;
}
//局部上升函数
void up(int x){
    int t=x;
    if(x/2>0&&heap[x/2]>heap[t]) t=x/2;
    if(t!=x){
        h_swap(t,x);
        up(t);
    }
}
//删除堆顶元素
void Delete_top(){
    h_swap(1,sizee);
    sizee--;
    down(1);
}
//删除第k个插入的数
void Delete(int k){
    int t=kp[k];
    h_swap(kp[k],sizee);
    sizee--;
    up(t);down(t);
}
//将第k个插入的数的值更新为x
void Upgrade(int k,int x){
    heap[kp[k]]=x;
    up(kp[k]);down(kp[k]);
}

哈希表

哈希表的作用:大空间映射到小空间(离散化是一种特殊的哈希方式)
-10^9到+10^9 (通过哈希函数)--->(映射) 0到10^5

一般的哈希函数:f(x)=x%N;(N是一个较大的质数)
为了方便并且可能出现负数,哈希函数可以写成:f(x)=(x%N+N)%N;

哈希表的存储结构一般有两种:拉链法和开放寻址法
哈希表一般支持的操作:添加和查找
注意:哈希表的删除==哈希表的查找+标记元素(不是真正意义上的删除)

大于10^5的最小质数为 10^5+3
大于2*10^5的最小质数为 2*10^5+3
大于3*10^5的最小质数为 3*10^5+7

拉链法实现哈希表(需要用链表实现):

const int N =1e5+3;//取大于1e5的第一个质数(使得冲突的概率最小)
int h[N],value[N],nextt[N],id;//开一个槽h,创建链表
void init(){
    memset(h,-1,sizeof h);//将槽先清空,空指针用-1来表示
}
void insert(int x){
    int k=(x%N+N)%N;//如果是负数,那它取模也是负的,所以+N再%N就一定是正数
    value[id]=x;
    nextt[id]=h[k];
    h[k]=id++;
}
bool find(int x){
    int k=(x%N+N)%N;//Hash函数,将x映射到0到1e5之间的数
    for(int i=h[k];i!=-1;i=nextt[i]){
        if(value[i]==x){
            return true;
        }
    }
    return false;
}

开放寻址法实现哈希表(开两到三倍的数组):

const int N=2e5+3;//数组开两到三倍
const int null=0x3f3f3f3f;//规定空指针为0x3f3f3f3f
//0x3f3f3f3f的十进制是1061109567,是大于10^9的,可以当作无穷大
int h[N];
void init(){//初始化
    //因为memset是按字节操作的,然而0x3f3f3f3f的每个字节都是0x3f
    //所以要把一段内存全部置为无穷大,只需memset(a,0x3f,sizeof(a))
    memset(h,0x3f,sizeof h);
}
//find函数返回的是这个数的位置
int find(int x) {
    int t=(x%N+N)%N;
    while(h[t]!=null&&h[t]!=x){//冲突情况:当前位置不为空并且不为x
        t++;
        if(t==N) t=0;//末尾情况就从头开始
    }
    return t;//位置是空的,则返回它本应该存储的位置
}
void insert(int x){//插入函数
    h[find(x)]=x;
}
bool check(int x){//判断查找是否成功函数
    if(h[find(x)]!=null) return true;
    else false;
}

字符串前缀哈希法(快速判断两个字符串的子串是否相同):

#include<iostream>
#include<cstring>
using namespace std;
typedef unsigned long long ULL;//ULL类型一般为64位,自动取模并且可以尽可能地减少冲突
const int N=1e5+5,P=131;
ULL h[N],p[N];
//h[i]:前i个字符的hash值,p数组:存储p的幂
//把字符串变成一个p进制数字(哈希值),实现不同的字符串映射到不同的数字
//P=131或13331 Q=2^64,大概率不会出现冲突,映射后的范围为:0到2^64-1
//作用:快速判断两个字符串的子串是否相同
ULL query(int l,int r){
    return h[r]-h[l-1]*p[r-l+1];//区间和公式
}
int main(){
    int n,m;cin>>n>>m;
    string s;cin>>s;
    //字符串从1开始编号,h[0]为0个字符的哈希值
    p[0]=1,h[0]=0;
    for(int i=0;i<n;i++){
        p[i+1]=p[i]*P;//更新权值
        h[i+1]=h[i]*P+s[i];//前缀和公式求整个字符串的哈希值
    }
    while(m--){
        int l1,r1,l2,r2;
        cin>>l1>>r1>>l2>>r2;
        if(query(l1,r1)==query(l2,r2)) cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
    return 0;
}