第 9 周 15、 异常检测(Anomaly Detection)

15.3 算法

在本节视频中，我将应用高斯分布开发异常检测算法。

异常检测算法：对于给定的数据集 $x^{(1)},x^{(2)},...,x^{(m)}$，我们要针对每一个特征计算 $\mu$和${\sigma }^2$的估计值。

$${\mu }_j=\frac{1}{m}\sum _{i=1}^m{x}_j^{(i)}$$
$${\sigma }_j^2=\frac{1}{m}\sum _{i=1}^m(x_j^{(i)}-{\mu }_j{)}^2$$

一旦我们获得了平均值和方差的估计值，给定新的一个训练实例，根据模型计算 𝑝(𝑥)：
$$p(x)=\prod _{j=1}^{n}p(x_j,{\mu }_j,{\sigma }_j^2)=\prod _{j=1}^1\frac{1}{\sqrt{2\pi {\sigma }_j^2}}{e}^{-\frac{(x_j-{\mu }_j{)}^2}{2{\sigma }_j^2}}$$

当𝑝(𝑥) < 𝜀时，为异常。
下图是一个由两个特征的训练集，以及特征的分布情况：

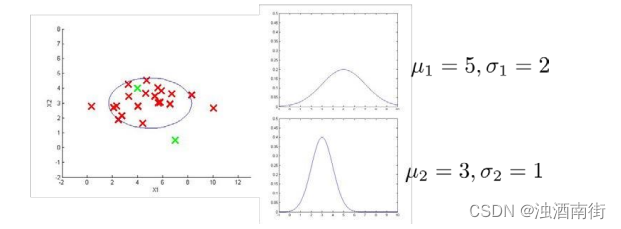
下面的三维图表表示的是密度估计函数，𝑧轴为根据两个特征的值所估计𝑝(𝑥)值：

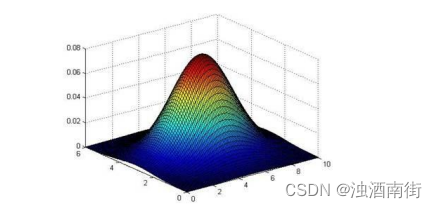
我们选择一个𝜀，将𝑝(𝑥) = 𝜀作为我们的判定边界，当𝑝(𝑥) > 𝜀时预测数据为正常数据，否则为异常。

在这段视频中，我们介绍了如何拟合𝑝(𝑥)，也就是 𝑥的概率值，以开发出一种异常检测算法。同时，在这节课中，我们也给出了通过给出的数据集拟合参数，进行参数估计，得到参数 𝜇 和 𝜎，然后检测新的样本，确定新样本是否是异常。

在接下来的课程中，我们将深入研究这一算法，同时更深入地介绍，怎样让算法工作地更加有效。

15.4 开发和评价一个异常检测系统

异常检测算法是一个非监督学习算法，意味着我们无法根据结果变量 𝑦 的值来告诉我们数据是否真的是异常的。我们需要另一种方法来帮助检验算法是否有效。当我们开发一个异常检测系统时，我们从带标记（异常或正常）的数据着手，我们从其中选择一部分正常数据用于构建训练集，然后用剩下的正常数据和异常数据混合的数据构成交叉检验集和测试集。

例如：我们有 10000 台正常引擎的数据，有 20 台异常引擎的数据。 我们这样分配数据：

6000 台正常引擎的数据作为训练集
2000 台正常引擎和 10 台异常引擎的数据作为交叉检验集
2000 台正常引擎和 10 台异常引擎的数据作为测试集

具体的评价方法如下：

1. 根据测试集数据，我们估计特征的平均值和方差并构建𝑝(𝑥)函数
2. 对交叉检验集，我们尝试使用不同的𝜀值作为阀值，并预测数据是否异常，根据 F1 值或者查准率与查全率的比例来选择 𝜀
3. 选出 𝜀 后，针对测试集进行预测，计算异常检验系统的𝐹1值，或者查准率与查全率之比。