1.返回倒数第k个节点
实现一种算法,找出单向链表中倒数第 k 个节点。返回该节点的值。
示例:
输入: 1->2->3->4->5 和 k = 2 输出: 4
说明:
给定的 k 保证是有效的。
1.1快慢指针
即慢指针一次走一步,快指针一次走两步,两个指针从链表起始位置开始运行,如果链表带环则一定会在环中相遇,否则快指针先走到链表的末尾
1.2解题代码
/*
快慢指针法 fast, slow, 首先让fast先走k步,然后fast,slow同时走,fast走到末尾时,slow走到倒数第k个节点。
*/
class Solution {
public:
ListNode* FindKthToTail(ListNode* pListHead, unsigned int k) {
struct ListNode* slow = pListHead;
struct ListNode* fast = slow;
while(k--)
{
if(fast)
fast = fast->next;
else
return NULL;
}
while(fast)
{
slow = slow->next;
fast = fast->next;
}
return slow;
}
};
2.链表的回文结构
对于一个链表,请设计一个时间复杂度为O(n),额外空间复杂度为O(1)的算法,判断其是否为回文结构。给定一个链表的头指针A,请返回一个bool值,代表其是否为回文结构。保证链表长度小于等于900。
测试样例:
1->2->2->1
返回:true
2.1解题思路
可以先找到中间节点,然后把后半部分逆置,在对前后两部分一一对比,如果节点的值全部相同,则即为回文。
2.2解题代码
class PalindromeList {
public:
bool chkPalindrome(ListNode* A) {
if (A == NULL || A->next == NULL)
return true;
ListNode* slow, *fast, *prev, *cur, *nxt;
slow = fast = A;
//找到中间节点
while (fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
}
prev = NULL;
//后半部分逆置
cur = slow;
while (cur)
{
nxt = cur->next;
cur->next = prev;
prev = cur;
cur = nxt;
}
//逐点比对
while (A && prev)
{
if (A->val != prev->val)
return false;
A = A->next;
prev = prev->next;
}
return true;
}
};2.3此题的另一种解法
可以先把链表中的元素值全部保存在数组中,然后再判断数组是否回文,不建议使用这种解法,因为如果没有告诉链表最大长度,则不能同此解法。
class PalindromeList {
public:
bool chkPalindrome(ListNode* A) {
// write code here
int a[900] = {0};
ListNode* cur = A;
int n = 0;
//保存链表元素
while(cur)
{
a[n++] = cur->val;
cur = cur->next;
}
//判断数组是否为回文结构
int begin = 0, end = n-1;
while(begin < end)
{
if(a[begin] != a[end])
return false;
++begin;
--end;
}
return true;
}
};
3.相交链表
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
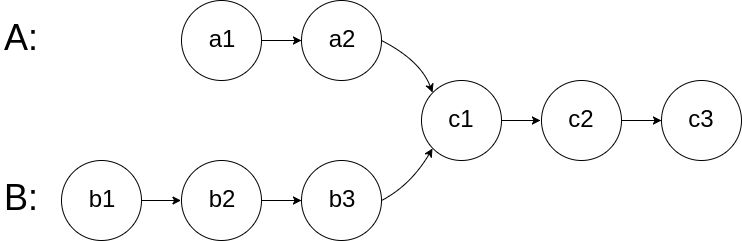
3.1解题思路
可以先计算出两个链表的长度,让长的链表先走相差的长度,然后两个链表同时走,直到遇到相同的节点,即为第一个公共节点。
3.2解题代码
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
int lenA = 0, lenB = 0;
struct ListNode* curA = headA, *curB = headB;
//计算链表长度
while(curA) {
++lenA;
curA = curA->next;
}
while(curB) {
++lenB;
curB = curB->next;
}
int gap = abs(lenA-lenB);
struct ListNode* longList = headA, *shortList = headB;
if(lenA < lenB) {
longList = headB;
shortList = headA;
}
//让长链表先走几步
while(gap--){
longList = longList->next;
}
//两个链表同时走,直到遇到相同的节点
while(longList && shortList)
{
if(longList == shortList) {
return longList;
}
else {
longList = longList->next;
shortList = shortList->next;
}
}
return NULL;
}4.随机链表的复制
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random --> y 。
返回复制链表的头节点。
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示Node.val的整数。random_index:随机指针指向的节点索引(范围从0到n-1);如果不指向任何节点,则为null。
你的代码 只 接受原链表的头节点 head 作为传入参数。
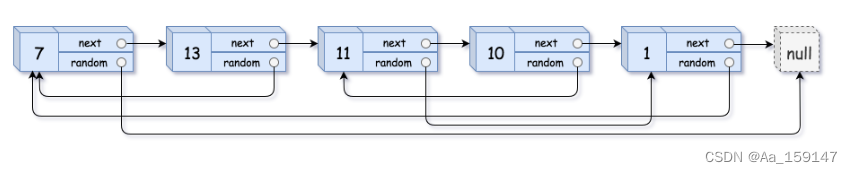
4.1解题思路
1.拷贝链表的每一个节点,拷贝的节点先链接到被拷贝节点的后面
2.复制随机指针的链接:拷贝节点的随机指针指向被拷贝节点随机指针的下一个位置
3.拆解链表,把拷贝的链表从原链表中拆解出来
4.2解题代码
class Solution {
public:
Node* copyRandomList(Node* head) {
// 1.拷贝链表,并插入到原节点的后面
Node* cur = head;
while(cur)
{
Node* next = cur->next;
Node* copy = (Node*)malloc(sizeof(Node));
copy->val = cur->val;
// 插入
cur->next = copy;
copy->next = next;
// 迭代往下走
cur = next;
}
// 2.置拷贝节点的random
cur = head;
while(cur)
{
Node* copy = cur->next;
if(cur->random != NULL)
copy->random = cur->random->next;
else
copy->random = NULL;
cur = copy->next;
}
// 3.解拷贝节点,链接拷贝节点
Node* copyHead = NULL, *copyTail = NULL;
cur = head;
while(cur)
{
Node* copy = cur->next;
Node* next = copy->next;
// copy解下来尾插
if(copyTail == NULL)
{
copyHead = copyTail = copy;
}
else
{
copyTail->next = copy;
copyTail = copy;
}
cur->next = next;
cur = next;
}
return copyHead;
}
};
5.环形链表|
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
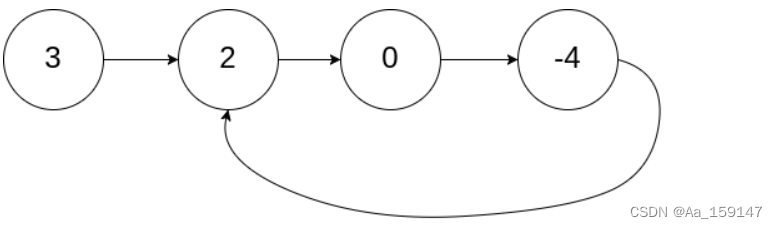
5.1解题思路
定义快慢指针fast,slow, 如果链表确实有环,fast指针一定会在环内追上slow指针。
5.2解题代码
typedef struct ListNode Node;
bool hasCycle(struct ListNode *head) {
Node* slow = head;
Node* fast = head;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
if(slow == fast)
return true;
}
return false;
}6. 环形链表||
6.1解题思路
如果链表存在环,则fast和slow会在环内相遇,定义相遇点到入口点的距离为X,定义环的长度为C,定义头到入口的距离为L,fast在slow进入环之后一圈内追上slow,
则会得知: slow所走的步数为:L + X fast所走的步数为:L + X + N * C
并且fast所走的步数为slow的两倍,故: 2*(L + X) = L + X + N * C
即: L = N * C - X 所以从相遇点开始slow继续走,让一个指针从头开始走,相遇点即为入口节点
6.2解题代码
typedef struct ListNode Node;
struct ListNode *detectCycle(struct ListNode *head) {
Node* slow = head;
Node* fast = head;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
//走到相遇点
if(slow == fast)
{
// 求环的入口点
Node* meet = slow;
Node* start = head;
while(meet != start)
{
meet = meet->next;
start = start->next;
}
return meet;
}
}
return NULL;
}7.拓展快慢指针
7.1快指针每次两步,慢指针每次一步
假设链表带环,两个指针最后都会进入环,快指针先进环,慢指针后进环。当慢指针刚进环时,可
能就和快指针相遇了,最差情况下两个指针之间的距离刚好就是环的长度。此时,两个指针每移动
一次,之间的距离就缩小一步,不会出现每次刚好是套圈的情况,因此:在满指针走到一圈之前,
快指针肯定是可以追上慢指针的,即相遇。
7.2 快指针走3步or4步....n步呢
假设快指针一次走3步,慢指针一次走两步
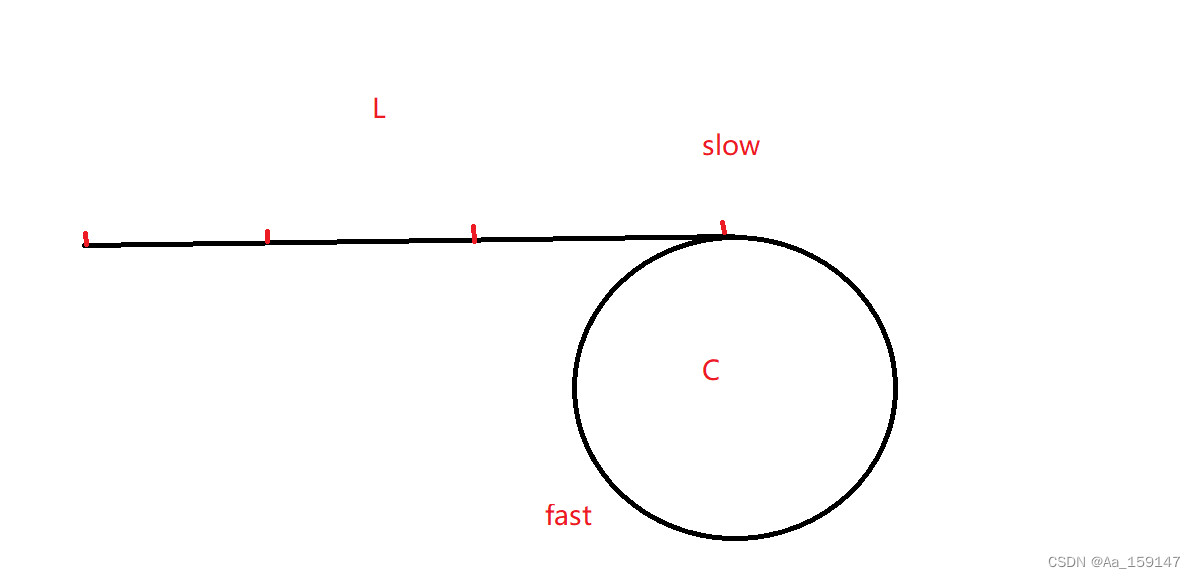
快慢指针之间的距离变化:
当N为偶数的时候:N-3 N-6 ............... 6 3 0
当N为奇数的时候:N-3 N-6 ................ 5 2 -1(当为-1时,则快慢指针刚好擦肩而过,此时距离变为C-1)
如若C-1为偶数,那么快慢指针相遇,如若C-1为奇数,那么快慢指针不会相遇
所以说:N为奇数,C为为偶数,则不可能相遇
是否存在此情况?
快指针一次走3步,慢指针一次走1步,此时快指针肯定先进环,慢指针后来才进环。
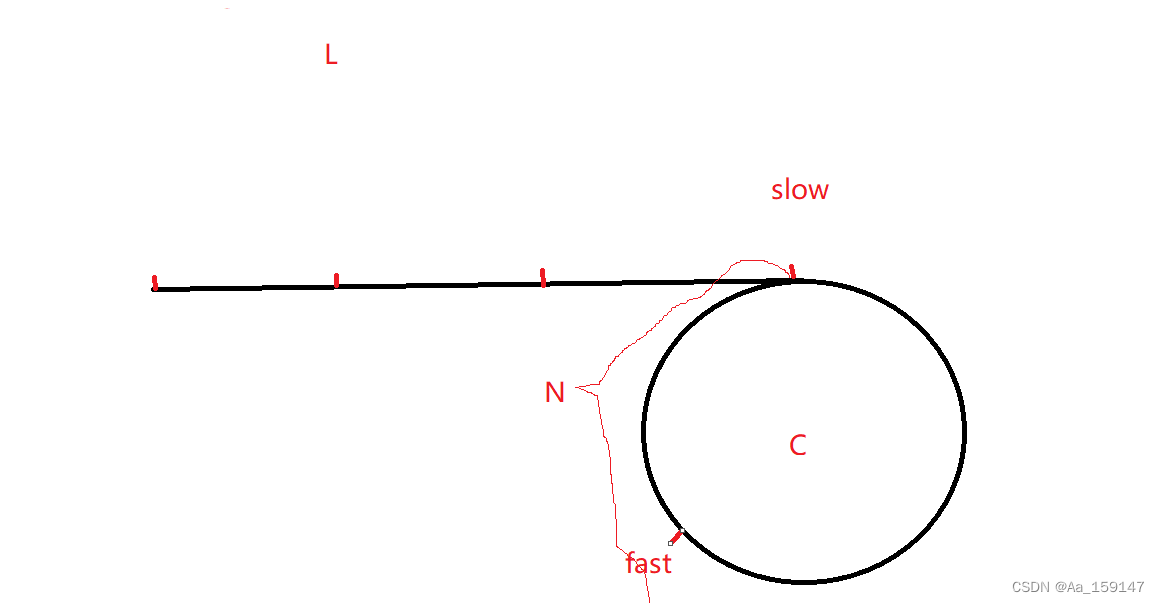
环的长度为C,环距头结点的距离是L,当slow刚进入环的时候与fast的距离是N
在判环时,快慢指针相遇是所走的路径长度:
slow刚进环时,有:
fast:L+n*C+C-N slow: L
注意:1.当慢指针进入环时,快指针可能已经在环中绕了几圈了,n至少为1
2.慢指针进入环之后,快指针肯定会在慢指针走一圈之内追上慢指针
因为:慢指针进入环后,快慢指针之间的距离最多就是环的长度,而两个指针在移动时。距离都在缩减。
fast每次走三步,所以路程是慢指针的三倍,所以有:
3L= L+n*C+C-N ------>>>2L = (n-1)C-N
等式左边是2L,永远是偶数,所以等式右边也必须是偶数,N为奇数,C为偶数,偶数乘以任意数也是偶数,则偶数 - 奇数不等一偶数,则不存在此情况
![[C++][数据结构]二叉搜索树:介绍和实现](https://img-blog.csdnimg.cn/direct/6f3eecc7fa6f472db3e13b17244bffa3.png)