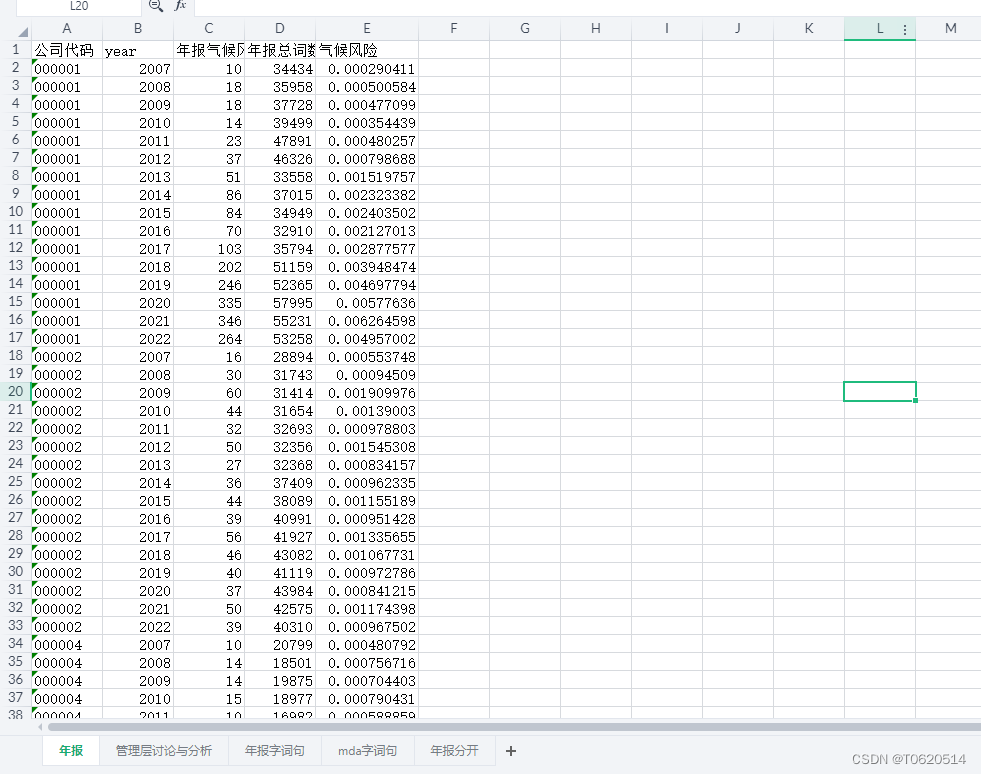
算法提高之方格取数

• 核心思想：数字三角形模型

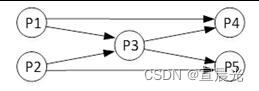
  • 考虑同时走两条路 用f[i1][j1][i2][j2]表示两条路取值

  • 因为两条路步数一定相同 即i1+j1 == i2+j2 设为k

    • 则f[k][i1][i2]即可表示两条路 k = n*2

  • 

    • dp方法如图

•   #include <iostream>
    #include <cstring>
    #include <algorithm>
    
    using namespace std;
    const int N = 11;
    int g[N][N],f[2*N][N][N];
    int n;
    
    int main()
    {
        cin>>n;
        int a,b,c;
        while(cin>>a>>b>>c , a||b||c) g[a][b] = c;
        
        for(int k=2;k<=2*n;k++)  //步数增加
            for(int i1=1;i1<=n;i1++)
                for(int i2=1;i2<=n;i2++)
                {
                    int j1=k-i1,j2=k-i2;  //取坐标
                    if(j1<1 || j2<1 || j1>n || j2>n) continue;  //出界
                    int &x = f[k][i1][i2];  //当前格子的f
                    int t = g[i1][j1];  //t为这一步要加的数
                    if(i1!=i2) t+=g[i2][j2];  //如果两条路在该点不重合 则两个格子的数都取
                    //dp
                    x = max(x,f[k-1][i1-1][i2-1]+t);
                    x = max(x,f[k-1][i1-1][i2]+t);
                    x = max(x,f[k-1][i1][i2-1]+t);
                    x = max(x,f[k-1][i1][i2]+t);
                }
        cout<<f[2*n][n][n]<<endl;
    }