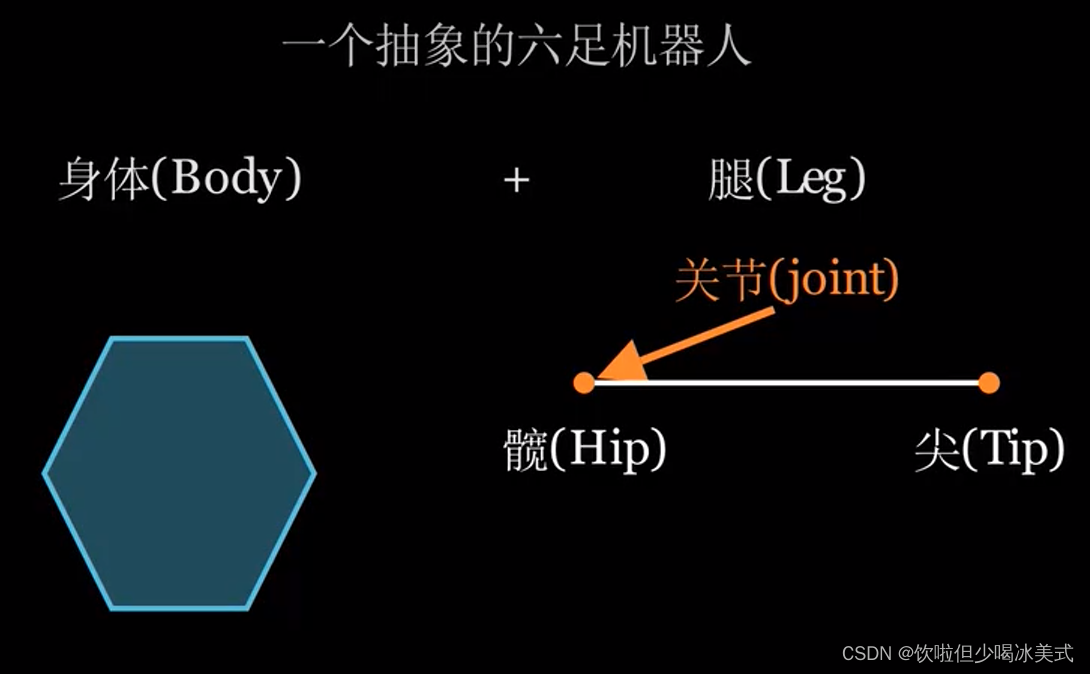

绕第一个顶点可以沿Z轴转动,角度用alpha表示

绕第二个点沿X轴转动,角度为Beta

第三个点沿X轴转动,记作gama
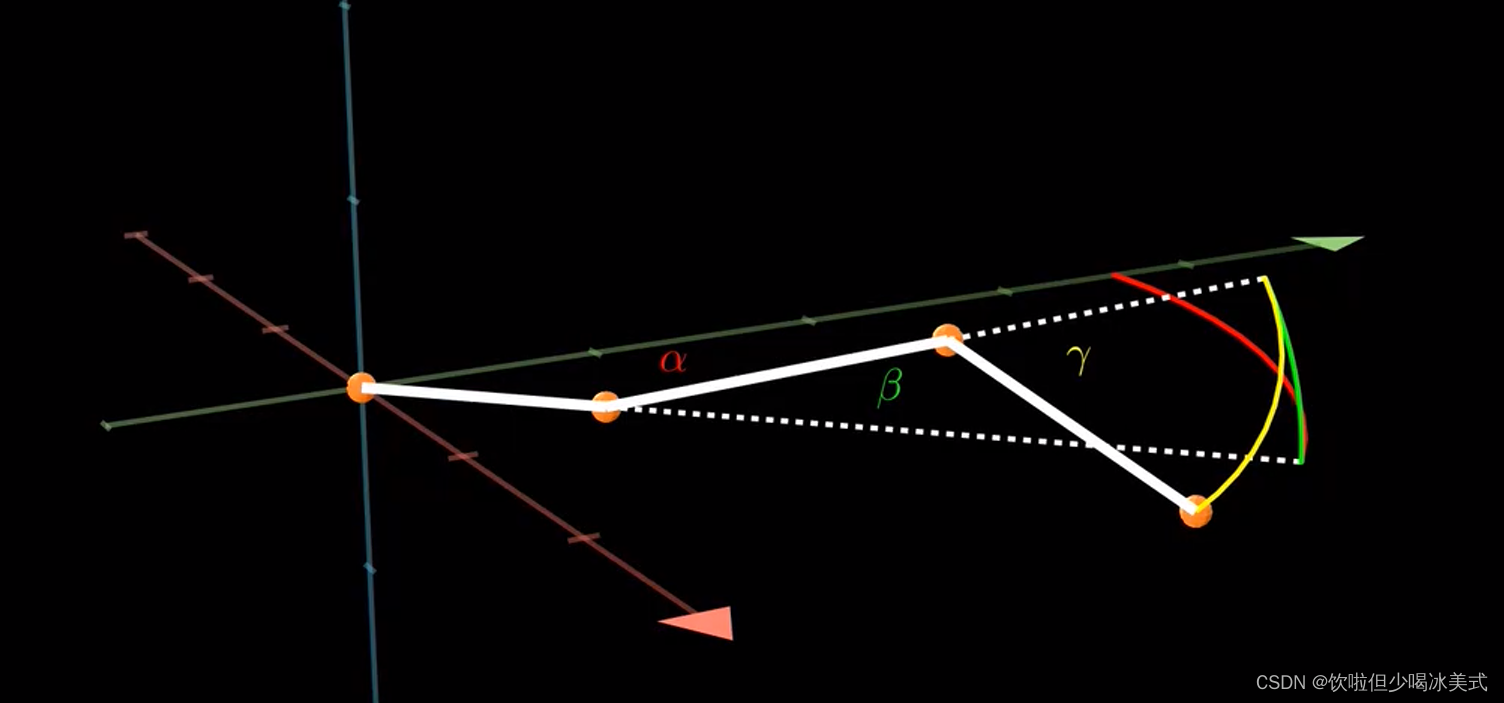
这三个点构成姿态(pose)
我们记第一个点为P0,画出它的本地坐标系,和世界坐标系一样红绿蓝分布代表XYZ

P0坐标系相当于绕Z轴旋转了alpha角度。因此,从世界坐标到此的变化可以写成齐次矩阵M0

其中Rz(alpha)表示绕z轴旋转alpha角所对应的旋转矩阵。

T描述的是腿部的整体平移
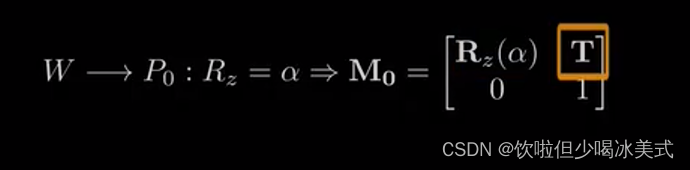
P1相对于P0是在Y方向上平移了L1长度,沿X轴旋转Beta角,所以世界坐标到P1的变换矩阵可以写作M1.


同理,P1到P2是x轴旋转gamma,y轴移动L2,P2到P3是y轴移动L3



这种已知alpha、beta、gamma三个角度来求解p3的过程,我们称之为正向运动学(forward kinematics)
反过来,如果我们知道P0和P3的位置,来求解这三个角度。这个过程就叫做反向运动学或逆运动学(inverse kinematics)
逆运动学
在实际应用中,逆运动学往往更加重要。我们经常已知tip尖端的位置,需要求得是角度。因为这个角度就是需要让舵机打到的角度。
比如,作为机器人的腿,尖端TIP就是与地面接触的,我们希望它可以抬起来往前走一步。于是我们规划尖端的运动轨迹,来反求角度对舵机进行控制。
另外,这其实也可以看成是一个机械臂,那么尖端就是手或者类似的抓取机构

我们通常能够结算目标的位置,通过舵机打角让机械臂的尖端到达目标位置。

下面我们来具体求解
首先,运动过程中腿是在一个平面内的,alpha角度会使这个平面绕Z轴旋转。
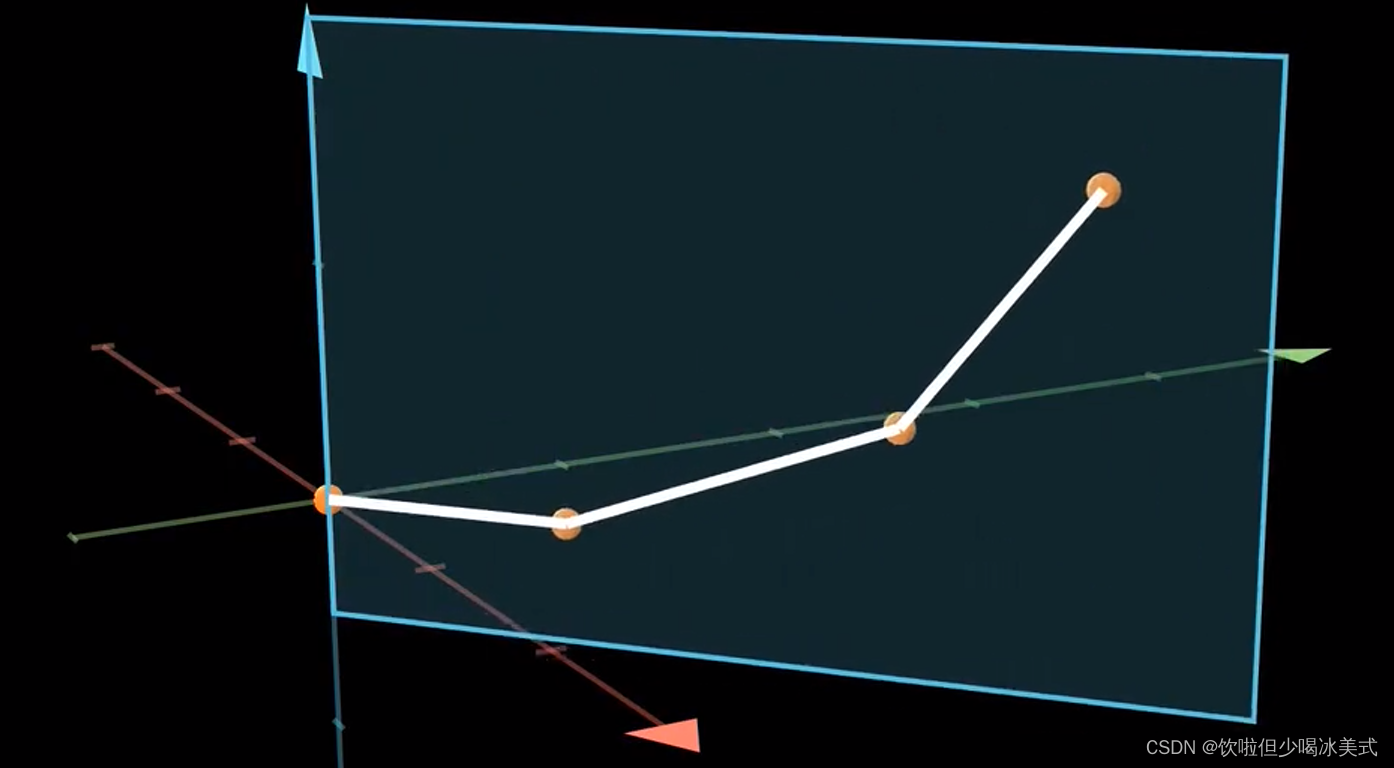
我们连接P0和P3,并记从P0到P3在XY平面上的投影向量为u

可得alpha角度就是向量u与y轴向量的夹角

我们从二维来看

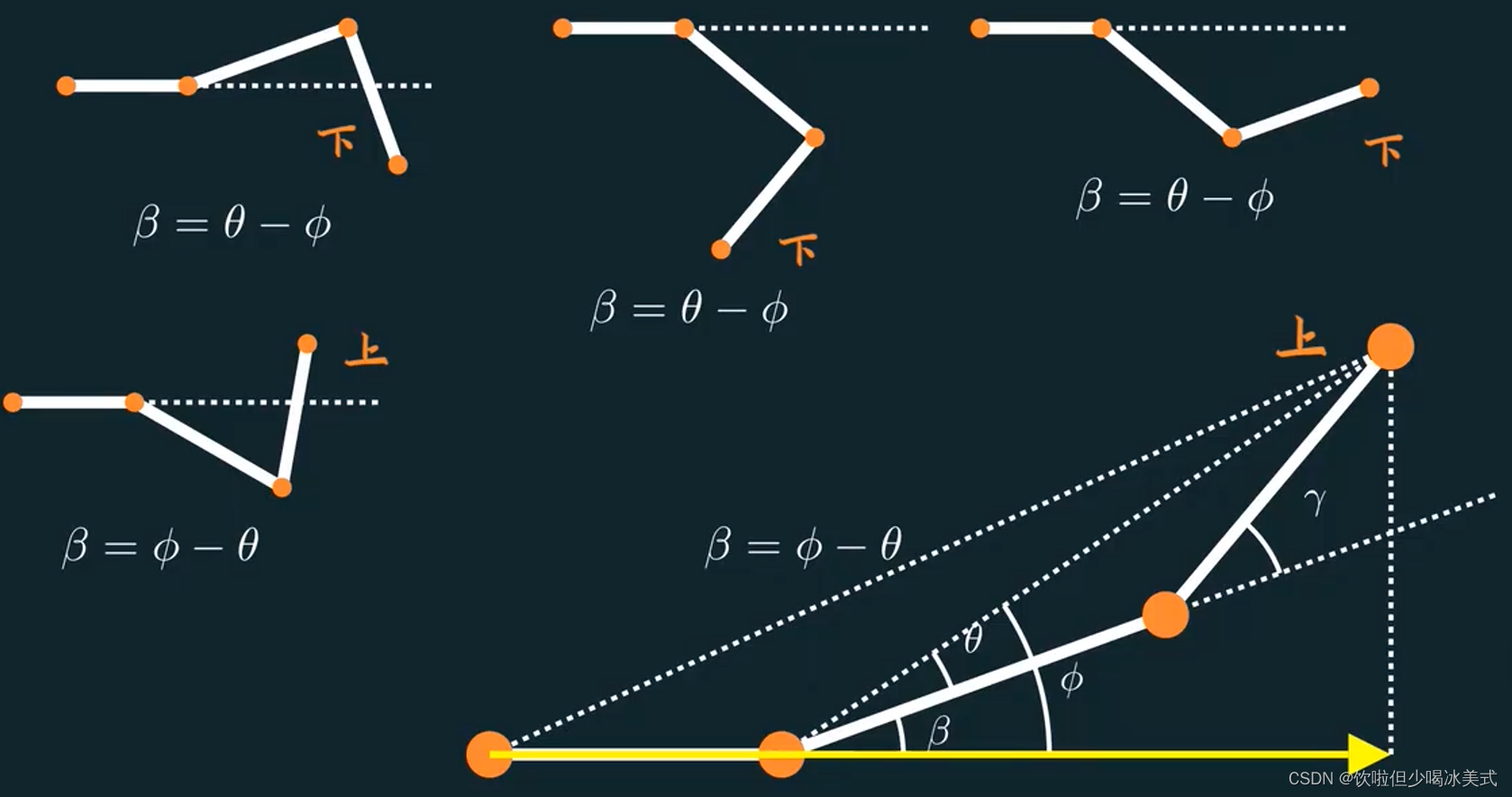
为了求belta和gamma,我们引入两个辅助角theta和phi



于是在三角形P1P2P3中,根据余弦定理可求theta

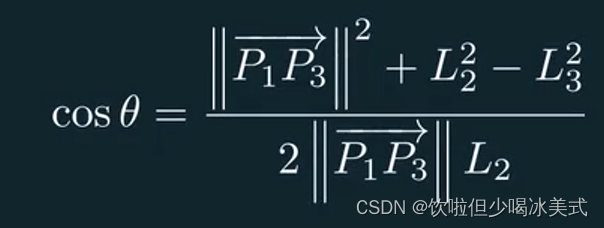
而phi是向量P1P3和向量u的夹角
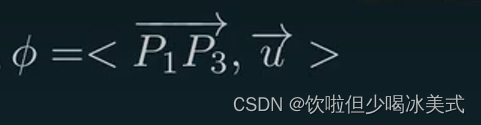
所以,易得beta是phi与theta的差

知道beta后可求P2的坐标。
就是P1的坐标在u方向上偏移L2乘以cosbeta的长度,在Z方向上偏移L2乘以sinbeta长度。

P2得到后就可求gamma,它是向量P1P2和向量P2P3的夹角

不过,这样计算还有个问题,就是如果P1P2P3攻线不能组成三角形的话。gamma等于多少呢?
那么gamma就一定为0,beta就是P1P3和u的夹角,这样连P2的坐标都不需要求了。

到这里还没完,因为beta、theta、phi并不是始终是这样的关系。
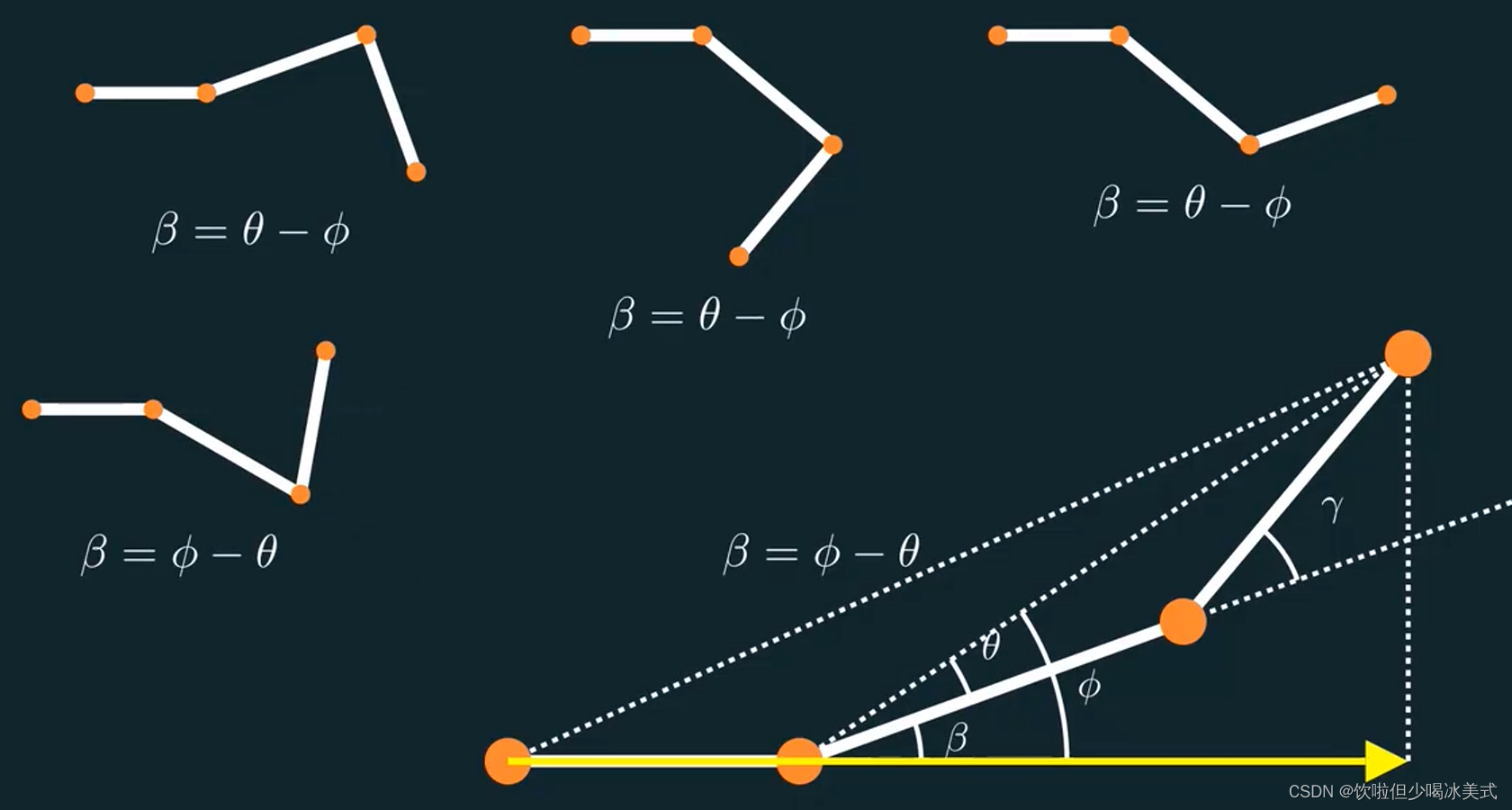
你会发现,其实只有两种情况,只要P3在u向量的上方,那么beta等于phi减去theta,否则beta等于theta减去phi