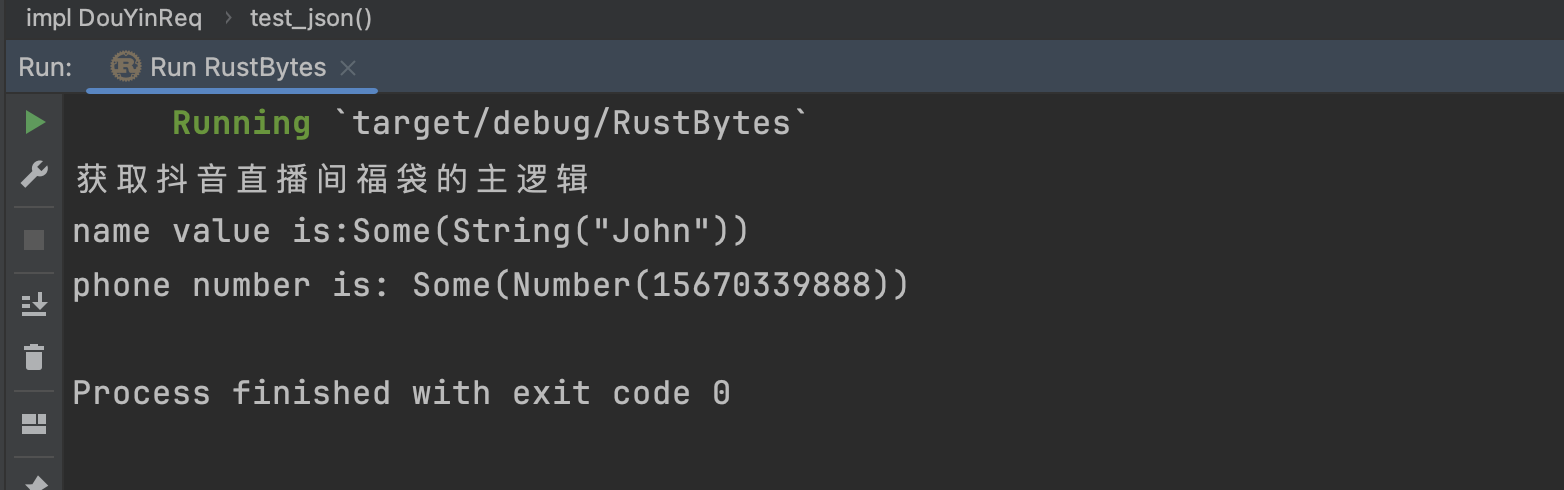
104 二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

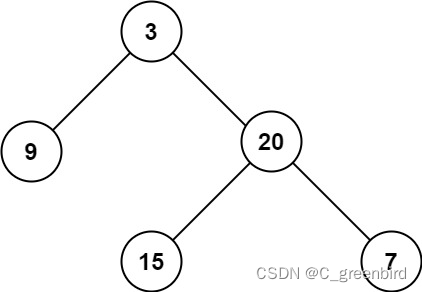
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：
输入：root = [1,null,2]
输出：2

提示：
树中节点的数量在 $[0,10^4]$ 区间内。
$-100<=Node.val<=100$

思路

（1）深度优先遍历DFS：
按深度往下遍历，先遍历左子树计算其深度l，再遍历右子树计算其深度r，那么该二叉树的最大深度就是max(l,r)+1。左右子树的深度也是如此计算，故用递归计算左右子树的最大深度+1即可。
（2）广度优先遍历BFS：
即二叉树的层次遍历，因为计算层数就可知道深度。不同于普通的层次遍历每次只取一个队列中的一个节点，计算深度需要每次取当前队列中的所有节点进行遍历。用ans记录深度。

代码

法一：

//DFS
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

法二：

// BFS
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        queue<TreeNode*> q;
        q.push(root);
        int ans = 0;
        while (!q.empty()) {
            int n = q.size();
            for (int i = 0; i < n; i++) {
                TreeNode* now = q.front();
                q.pop();
                if (now->left) {
                    q.push(now->left);
                }
                if (now->right) {
                    q.push(now->right);
                }
            }
            ans++;
        }
        return ans;
    }
};