在实际的工程应用中，往往会进行大量的数学运算。运算时除了会用到整数，很多时候也会用到小数。而我们知道在数字电路底层，只有「高电平1」和「低电平0」的存在，那么仅凭 0和1 该如何表示小数呢？

数字电路中，小数可以用两种形式来表示：「定点数」和「浮点数」。浮点数的内容我们下篇文章再讲，本文只讲定点数。

什么是定点数？

首先要明确的是，「定点数」的说法是相对「浮点数」来说的。要理解什么是定点数，可以先从要理解它的名字开始–定是什么？点又是什么？

「定点数」是英语「fixed-point number」的中文翻译，fixed的意思是固定的，point的意思是小数点，所以「定点数」其实也可以叫「固定小数点的数」。同样的，「浮点数」自然就是「浮动小数点的数」。

在10进制中，小数的表示是通过小数点和它所在位置来实现的。比如12.5，它表示的值是十二点五；而1.25则是一点二五。尽管12.5和1.25都用了「1 2 5」这3个数来表示，但由于小数点位置的不同，使得前者的数值是后者的十倍。

遗憾的是，电路只能表示1和0，无法直接表示小数点，所以上面的方法在电路中是行不通的。

假如你现在收到一条信息「我传一个小数过来，10100111」，看到这样一条信息，你恐怕只会觉得莫名其妙！10100111是哪门子小数？慢着，10100111如果直接转换成10进制数就是167，167当然不是小数，因为它没有小数点。但是仔细想想？它真的没有小数点吗？如果把167看做是167.0呢？也就是默认它的小数点是在最右边呢？

接着你很快又收到了第二条信息「我再传一个小数过来，10100111，它的小数点在从右往左数第1位」。这次你终于能看懂了 ，这不就是1010011.1吗？也就是10进制数83.5。那么直接说83.5不就完事了吗？说这么多干吗？

然后是第三条消息「我再传一个小数过来，10100111，它的小数点在从右往左数第2位」。这次传的是101001.11，即10进制数41.75。

······（省略后面的10086条消息）······

看到这是不是清晰很多了–尽管我们无法直接用小数点来表示2进制小数，但可以通过指定小数点的位置来说明这是一个小数啊！

约定小数点的位置，且这个位置固定不变，小数点前、后的数字，分别用2进制表示，组合起来就可以用来表示和使用2进制小数了。用这种方式表示的数就叫做「定点数」。

定点数如何表示数字？

很容易想到，定点数除了能表示小数外，也可以表示整数。因为你可以把小数点的位置约定在最右面，这样其实相当于没有小数点，所以表示的都是整数；同样的，你也可以把小数点规定在最左边，这样表示的就是一个整数部分为0的小数。

所以定点数的表示可以分为三种情况：

纯整数

这种情况约定小数点在最右边。例如10进制数85用8位无符号2进制数表示就是0101_0101，因为小数点在最右边，所以可以看做是0101_0101.0 。

纯小数

定点纯小数是指整数部分为0的小数。根据是无符号数还是有符号数，分为两种情况：

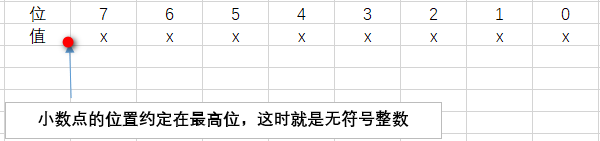
（1）无符号数

无符号数的最高位不表示符号，仅表示数值。这种情况约定小数点的位置在最左边。例如10进制数0.125用8位无符号2进制数表示就是0.0010_0000，因为小数点在最左边，所以是0010_0000。

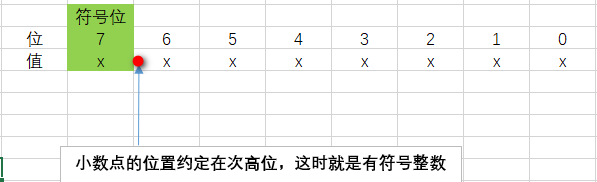
（2）有符号数

有符号数的最高位表示符号，不表示数值。这种情况约定小数点的位置在次高位。例如10进制数-0.125用8位无符号2进制数表示就是1.0010_000，因为小数点在次高位，所以是1010_0000。

整数 + 小数

除了纯整数和纯小数这两种情况外，其实定点数主要是用来表示 「整数 + 小数」的情况，例如3.14、1.5、25.125等等。这种情况需要确定以下信息才能正确表示该数：

• 整数部分长度
• 小数部分长度
• 是否有符号位

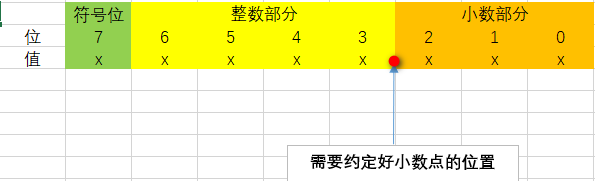
整数和小数的长度之和确定了用多大的电路来表示定点数，而二者的长度之比则确定了小数点的位置。符号位则确定了该数是一个有符号数还是一个无符号数。

光说不练云玩家，接下来看几个例子。

（1）1.25 的定点数表示

首先约定用无符号数来表示，然后约定5 位为整数部分，3 位为小数部分。所以有：

1.25(D) = 1.01(B) = 00001.010 = 00001010

（2）-9.5 的定点数表示

首先需要用有符号数来表示，因为整数9需要4位来表示，而小数0.5仅需1位就可表示。为此可以约定5位为整数部分（注意最高位为符号位），3 位为小数部分。所以有：

-9.5(D) = 10110.1(B) = 10110.100 = 10110100

定点数的数值范围

定点数用来表示小数很方便，但是它也有个很大的问题–它的表示范围很小。

以5 位表示整数部分，3 位表示小数部分的无符号定点数为例，它的整数部分可以表示的范围是00000-11111，即0-31，步长是1；小数部分的范围是0.000-0.111，即0-0.875，步长是0.125。综合起来范围是0-31.875，步长为0.125。

有符号数的因为是用补码表示，所以它的范围取值比较特殊。以5 位表示整数部分，3 位表示小数部分的有符号定点数为例，它能表示的最小值是10000_000，即-32，它能表示的最大值是01111_111，即15.875。

若以m表示定点数的整数位宽（m不包含符号位），以n表示定点数的小数位宽，则有符号数和无符号数的定点数的表示范围为：

有符号数	-2^m ~ （2^m - 2^-n）
无符号数	0 ~ （2^m - 2^-n）

如果想表示更大范围、更高精度的值，怎么办？

• 扩大整体位宽：比如使用 16位、32位来表示， 这样相应地整数部分和小数部分的宽度都可以增加，自然表示范围也就变大了。但是位宽的增加，也会带来更多的硬件开销
• 改变小数点的位置：小数点向后移动，那么整个数字范围就会扩大，但是小数部分的精度就会越来越低。小数点向前移，表示的精度会变高，但是数字的表示范围又会降低。所以说定点数小数点位置的确定是一个范围和精度的trade off（权衡）

一些定点数的表示格式

除了可以用类似「以5 位表示整数部分，3 位表示小数部分的无符号定点数」的语言来描述定点数的格式外，还有多种定点数的表示格式。常见的有以下几种：

Q格式（Q notation）

Q格式的一般形式是：

Qm.n

默认情况下，用Q格式描述的都是有符号定点数。其中m表示整数部分的长度（这个值不包括符号位），n表示小数部分的长度。所以用Q格式描述的定点数的整体长度为：

w = m + n + 1 //整数部分长度 + 小数部分长度 + 符号位长度

例如 「 Q3.12 」描述的是一个整体长度为16位的2进制有符号定点数，它的整数部分长度是3，而小数部分长度是12。根据小数部分的长度，可以推断出分辨率为 2^-12。

在Q前面加一个 U 即可用来表示无符号的2进制定点数。例如 「 UQ1.15」描述的就是一个整数部分长度为1，小数部分长度为15的无符号的2进制定点数。

整数部分的长度值和小数点可以被省略，而只描述小数部分的长度。例如「 Q12 」描述的就是一个小数部分长度是12的2进制有符号定点数，但是它的整体长度是不确定的，你可以额外指定整体长度，或者说整体长度就取决于存储这个定点数的寄存器。

如果这个定点数存储一个16位的寄存器，那它的值就是：

xxxx . xxxx_xxxx_xxxx

如果这个定点数存储一个32位的寄存器，那它的值就是：

xxxx_xxxx_xxxx_xxxx_xxxx_xxxx . xxxx_xxxx_xxxx

其实也可以看出来，这种表示方法就是把它的值乘以 2^-12 。

这种整数长度m不包括符号位的Q格式主要是TI公司的DSP在使用，ARM公司也有一种类似的Q格式，但是它的整数长度m是包含符号位的。表示方式的不同不是什么大不了的事，只要是使用过程中确定好了就行，为此你甚至也可以自己创造一套定点数表示方式（只要不怕没人用就行，嘿嘿）。

S表示法

S表示法的一般形式是：

Sm.n

其中S表示这是一个有符号的定点数，m表示整数位数（m不包括符号位），n表示小数位数。这种方法其实跟Q格式很像，只不过它的表示无符号定点数的方法不是在前面加 U ，而是去掉 S，像这样：

m.n

例如「 2.4 」表示的就是一个整数位数为2，小数位数为4的无符号定点数。

总结

总的来说，用定点数表示的小数，不仅数值的范围表示有限，而且其精度也很低。要想解决这 2 个问题，人们就提出了使用「浮点数」的方式表示数字，关于浮点数的表示方法，我们会在下一篇文章进行讲解。

定点数和浮点数都可以表示小数，而定点数的精度固定，表现范围比较有限；但是，定点数在硬件上比较容易实现，在实际的数据算法中，定点数运算效率比浮点数的运算效率高很多，同时定点数使用的资源也比较少。因此，定点数被广泛地应用在数字信号处理的各种应用场景中。

1. 定点数是在计算机中表示数字的一种方式，它既可以表示整数，也可以表示小数
2. 在固定 bit 下，约定小数点的位置，然后把整数部分和小数部分分别转换为二进制，就是定点数的结果
3. 受限于小数点的位置，用定点数表示小数时，数值的范围和小数精度是有限的
4. 在现代计算机中，定点数通常用来表示整数，对于高精度的小数，通常用浮点数表示