一、题目

描述

    每年六一儿童节，牛客都会准备一些小礼物和小游戏去看望孤儿院的孩子们。其中，有个游戏是这样的：首先，让 n 个小朋友们围成一个大圈，小朋友们的编号是0~n-1。然后，随机指定一个数 m ，让编号为0的小朋友开始报数。每次喊到 m-1 的那个小朋友要出列唱首歌，然后可以在礼品箱中任意的挑选礼物，并且不再回到圈中，从他的下一个小朋友开始，继续0... m-1报数....这样下去....直到剩下最后一个小朋友，可以不用表演，并且拿到牛客礼品，请你试着想下，哪个小朋友会得到这份礼品呢？

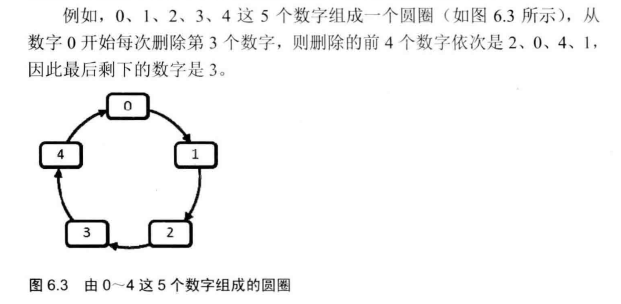
数据范围：1≤𝑛≤50001≤n≤5000，1≤𝑚≤100001≤m≤10000

要求：空间复杂度 𝑂(1)O(1)，时间复杂度 𝑂(𝑛)O(n)

示例1

输入：

5,3

返回值：

3

示例2

输入：

2,3

返回值：

1

说明：

有2个小朋友编号为0，1，第一次报数报到3的是0号小朋友，0号小朋友出圈，1号小朋友得到礼物  

示例3

输入：

10,17

返回值：

2

二、思路解析

这道题，我们可以通过模拟的方式来解决，但是直接模拟的话时间复杂度可能会较高。所以我们需要找到一种更高效的方法。

观察规律发现，每轮游戏中，第一个出列的小朋友编号总是在上一轮的基础上增加了 m-1。

假设在第 i 轮游戏中，第一个出列的小朋友的编号为 f(i)，那么在第 i+1 轮游戏中，第一个出列的小朋友的编号为 f(i+1) = (f(i) + m) % n。

利用这个规律，从后往前推导，我们便能得到最后剩下的小朋友的编号。

三、完整代码

import java.util.*;


public class Solution {

    public int LastRemaining_Solution (int n, int m) {

        int ret = 0;
        int f = 0;
        for(int i = 2; i <= n; i++){
            f = (f + m) % i;
        }

        return f;
    }
}

以上就是本篇博客的全部内容啦，如有不足之处，还请各位指出，期待能和各位一起进步！