前缀和(Prefix Sum)和差分(Difference)是两种常用的数组操作,用于解决一些求和、求区间和、区间修改等问题。
前缀和是指一个数组中每个位置上的元素与它前面位置上所有元素的和。例如,数组nums=[1, 2, 3, 4, 5]的前缀和数组为prefix=[1, 3, 6, 10, 15],其中prefix[i]表示nums中前i个元素的和。我们可以通过一次遍历数组来计算前缀和,时间复杂度为O(n)。
差分是指一个数组中每个位置上的元素与它前面位置上的元素的差。例如,数组nums=[1, 2, 3, 4, 5]的差分数组为diff=[1, 1, 1, 1, 1],其中diff[i]表示nums中第i个元素与第i-1个元素的差。我们可以通过一次遍历数组来计算差分,时间复杂度为O(n)。
前缀和和差分可以相互转换。给定一个前缀和数组prefix,我们可以通过计算差分数组diff来还原原始数组nums。具体方法是,我们可以通过一次遍历prefix计算diff数组,其中diff[i]=prefix[i]-prefix[i-1](特别地,diff[0]=prefix[0])。给定一个差分数组diff,我们可以通过计算前缀和数组prefix来还原原始数组nums。具体方法是,我们可以通过一次遍历diff计算prefix数组,其中prefix[i]=prefix[i-1]+diff[i](特别地,prefix[0]=diff[0])。
前缀和和差分的应用非常广泛。其中,前缀和可以用于快速计算数组中某个区间的和,时间复杂度为O(1)。差分可以用于快速修改数组中某个区间的元素。通过修改差分数组,我们可以在O(1)的时间内完成区间修改操作。总之,前缀和和差分是编程中非常有用且灵活的数组处理技巧。
一维前缀和:
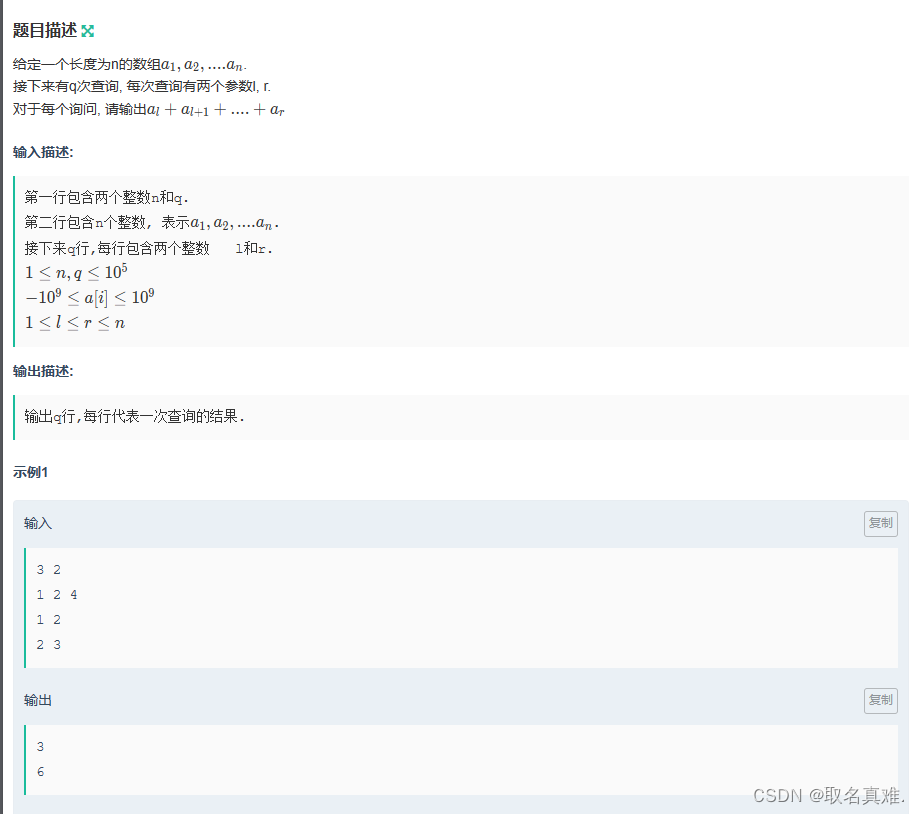
#include<iostream>
#include<cstring>
using namespace std;
const int N=1e5+10;
int n,q;
long long a[N],sum[N];
int main()
{
memset(sum,0,sizeof(sum));
cin>>n>>q;
for(int i=1;i<=n;i++)
{
cin>>a[i];
sum[i]=sum[i-1]+a[i];
}
while(q--)
{
int a,b;
cin>>a>>b;
cout<<sum[b]-sum[a-1]<<endl;
}
}二维前缀和:

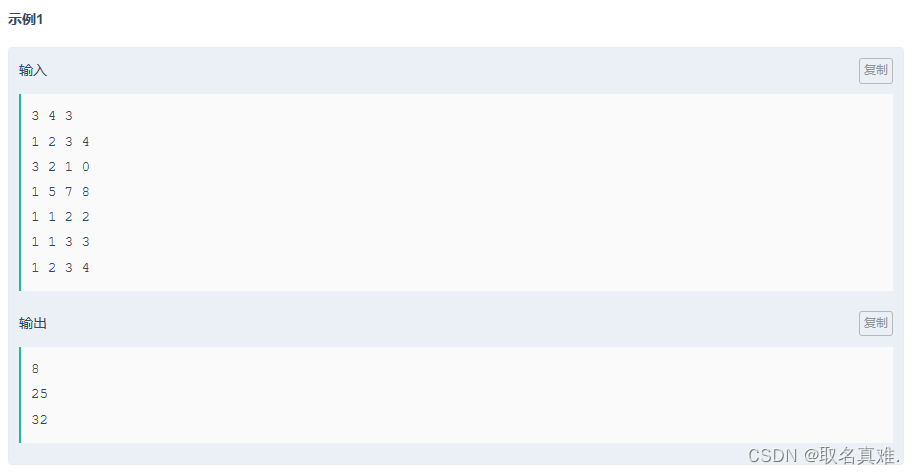
#include<iostream>
using namespace std;
const int N=1e3+10;
int a[N][N];
long long s[N][N];
int n,m,q;
int main()
{
cin>>n>>m>>q;
for(int i=1;i<=n;++i)
for(int t=1;t<=m;++t)
cin>>a[i][t];
for(int i=1;i<=n;++i){
for(int t=1;t<=m;++t){
s[i][t]=s[i-1][t]+s[i][t-1]-s[i-1][t-1]+a[i][t];
}
}
int x1,x2,y1,y2;
while(q--){
cin>>x1>>y1>>x2>>y2;
cout<<s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]<<endl;
}
return 0;
}一维差分:
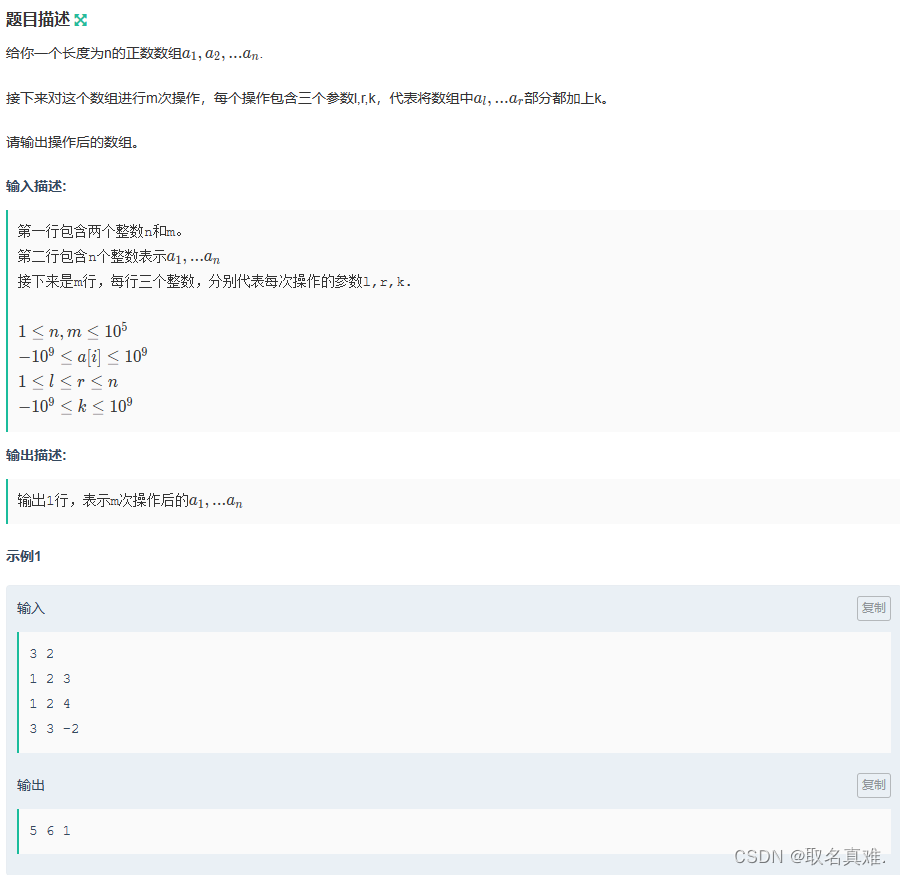
#include<iostream>
using namespace std;
const int N=1e5+10;
int n,m;
long long a[N],dp[N];
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
dp[i]=a[i]-a[i-1];
}
while(m--)
{
int a,b,k;
cin>>a>>b>>k;
dp[a]+=k;
dp[b+1]-=k;
}
for(int i=1;i<=n;i++)
{
dp[i]+=dp[i-1];
cout<<dp[i]<<" ";
}
}二维差分:

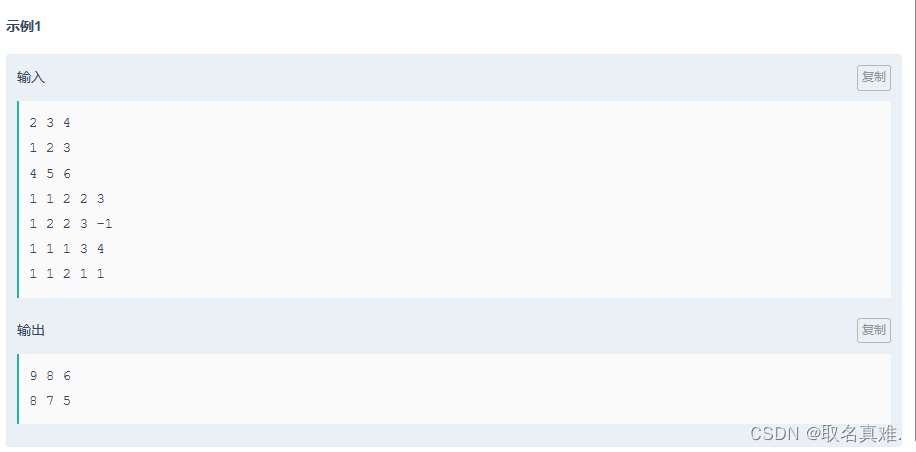
#include<iostream>//从三个方向来加
using namespace std;
const int N=1e4+10;
int n,m,q,x1,x2,y1,y2,k;
long long a[N][N],dp[N][N],ans[N][N];
/*
k 。
。。-k
-k k
*/
int main()
{
cin>>n>>m>>q;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>a[i][j];
while(q--)
{
cin>>x1>>y1>>x2>>y2>>k;
dp[x1][y1]+=k;
dp[x1][y2+1]-=k;
dp[x2+1][y1]-=k;
dp[x2+1][y2+1]+=k;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
ans[i][j]=dp[i][j]+ans[i-1][j]+ans[i][j-1]-ans[i-1][j-1];
cout<<a[i][j]+ans[i][j]<<" ";
}
cout<<endl;
}
}