阅读目录
- 1. 题目
- 2. 解题思路一
- 3. 代码实现一
- 4. 解题思路二
- 5. 代码实现二
1. 题目

2. 解题思路一
参考 剑指 Offer——数组中的逆序对,我们依然借助于归并排序中的合并操作来计算某个元素右侧小于它的元素个数。
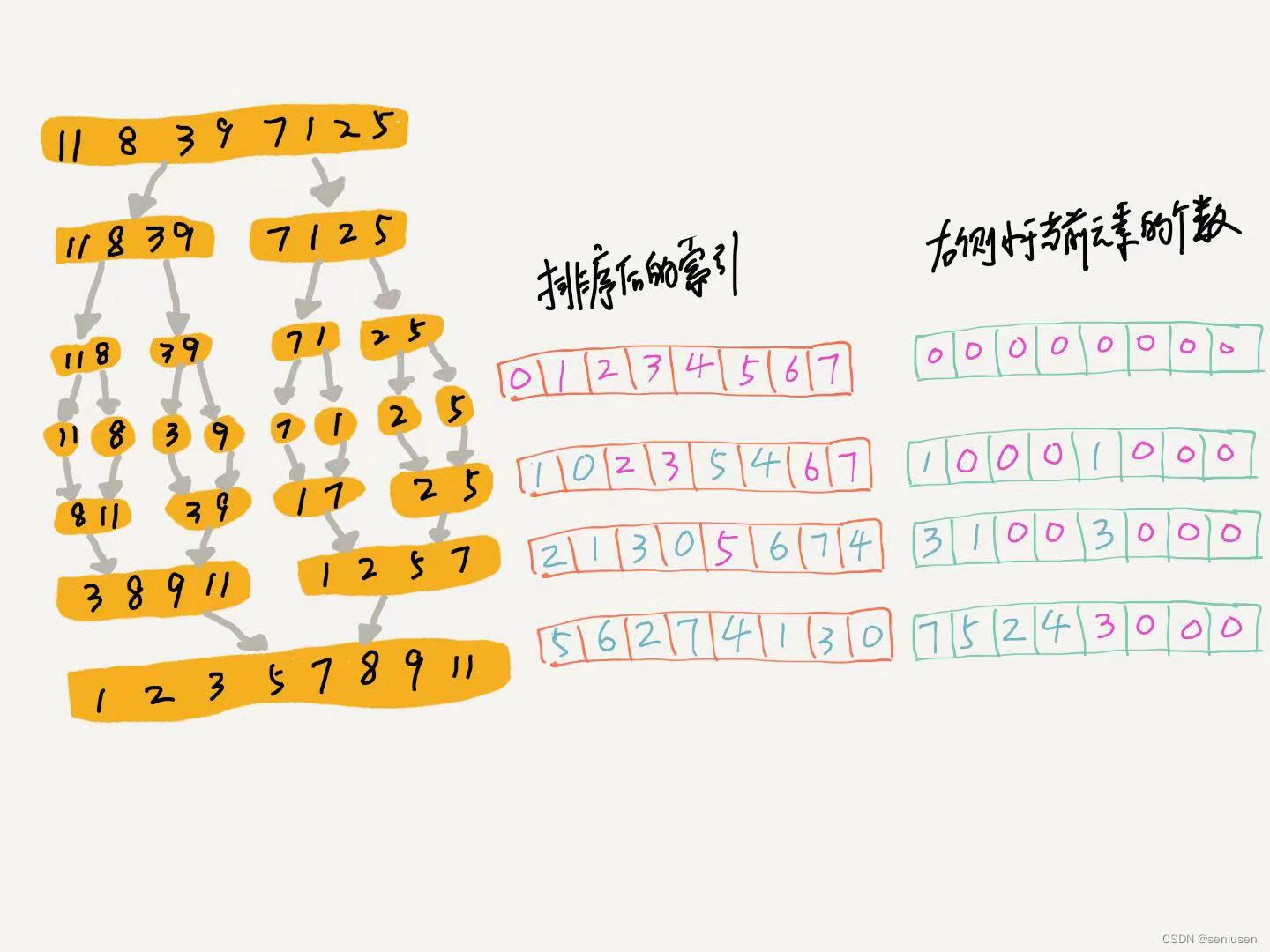
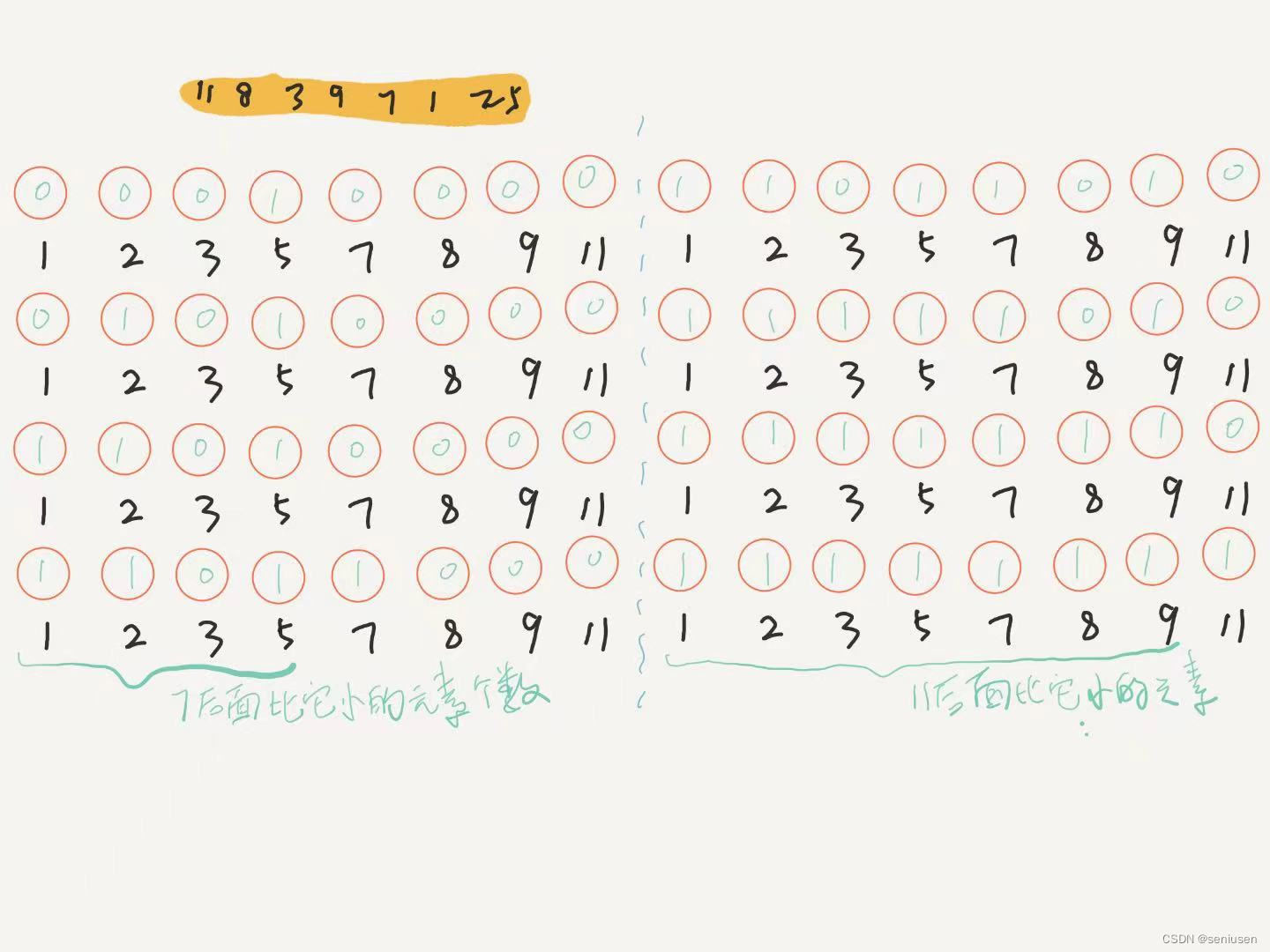
如上图最左边所示,第五行开始进行第一次合并过程。因为 11 > 8 11>8 11>8,所以, 11 11 11 右边小于它的元素个数加 1 1 1,也就是上图最右侧第二行的数组(我们记为 c o u n t s counts counts 数组)第 0 0 0 个元素变为 1 1 1。同理,数字 7 7 7 所在的位置,数组的第 4 4 4 个元素也要加 1 1 1 。
这次合并后,有一些元素的位置更改了,比如 11 11 11 变到了第 1 1 1 个位置,后面合并过程如果再遇到有比 11 11 11 小的元素,我们需要对 c o u n t s [ 0 ] counts[0] counts[0] 的值进行更改(也就是 11 11 11 在原数组中的位置 0 0 0),而不是修改 c o u n t s [ 1 ] counts[1] counts[1] (也就是 11 11 11 在当前合并后的位置 1 1 1)。
所以,我们还需要一个索引数组来记录每个数字在原始数组中的索引位置,这里我们记为 s r c _ i n d e x src\_index src_index 数组,也就是上图中间的数组,这样,不管数字 11 11 11 在排序后变到了哪个位置,我们都可以获取到它的原始索引。
继续往后看,下一步,我们需要合并左边的有序数组 [ 8 , 11 ] [8, 11] [8,11] 和右边的有序数组 [ 3 , 9 ] [3, 9] [3,9],首先,我们判断出 8 > 3 8>3 8>3,那么 8 8 8 以及它后面的元素对应的 c o u n t s counts counts 数组的值都需要增 1 1 1。然后 8 < 9 8<9 8<9,不需要做什么。最后, 11 > 9 11>9 11>9,那么 11 11 11 对应的 c o u n t s [ 0 ] counts[0] counts[0] 继续增 1 1 1 变为 3 3 3。
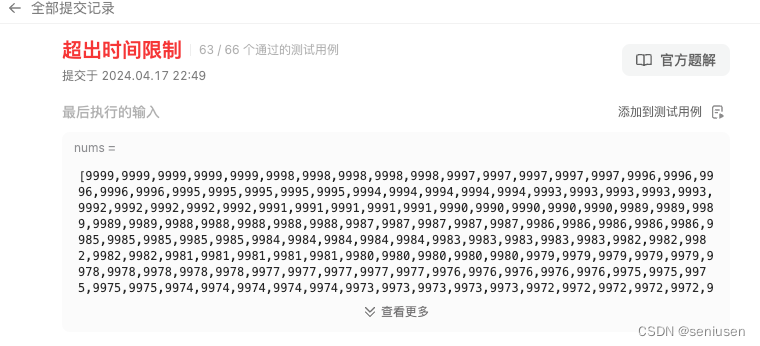
这样理解起来没什么问题,但若是实现代码,那么每次遇到右边元素比左边小,我们都需要循环左边有序区间还未进行归并的元素,来对它们的 c o u n t s counts counts 数组进行修改,这样每次归并过程就不是只访问所有待合并元素一遍,那么总的算法时间复杂度也就不是 O ( n l o g n ) O(nlogn) O(nlogn) 了, LeetCode 上部分测试用例也会通不过,会报一个超出时间限制的错误,如下图所示。
我们换个思路,只在归并到左边区间元素的时候更新 c o u n t s counts counts 数组即可。还是上面的过程,首先,我们判断出 8 > 3 8>3 8>3,这时候需要放置右边的元素 3 3 3,所以我们什么都不做。然后 8 < 9 8<9 8<9,我们需要放置左边的元素 8 8 8,这时候我们去检查右边区间的元素已经放置了多少个,那么 c o u n t s counts counts 数组就需要增加多少,发现右边只放了一个 3 3 3,所以 c o u n t s [ 1 ] + = 1 counts[1]+=1 counts[1]+=1 。继续判断 11 > 9 11>9 11>9,需要把 9 9 9 放置过去, c o u n t s counts counts 数组不变。最后,我们需要放置左边的元素 11 11 11,这时候发现右边区间放置了 3 , 9 3, 9 3,9 两个元素 ,所以 c o u n t s [ 0 ] + = 2 counts[0]+=2 counts[0]+=2 。
3. 代码实现一
class Solution {
public:
vector<int> sorted_nums; // 合并过程中存放元素的临时数组
vector<int> counts; // 存放结果
vector<int> src_idxs; // 存放排序后元素对应的原始索引
vector<int> sorted_idxs; // 合并过程中存放元素原始索引的临时数组
void MergeArray(vector<int>& nums, int left, int mid, int right) {
int i = left;
int j = mid + 1;
int st = 0;
while (i <= mid && j <= right) {
if (nums[i] <= nums[j]) {
// 正确做法是在放置左边元素的时候,一次性更新counts数组
// 这时候,右边区间[mid+1, j)位置的元素都比左边当前元素小
counts[src_idxs[i]] += j - mid - 1;
sorted_idxs[st] = src_idxs[i];
sorted_nums[st++] = nums[i++];
} else {
// 这里,每次遇到右边元素比左边元素小
// 就更新左边区间当前元素及后面元素的counts数组
// 时间复杂度不满足O(nlogn),会超时
// for (int m = i; m <= mid; ++m) {
// counts[src_idxs[m]]++;
// }
sorted_idxs[st] = src_idxs[j];
sorted_nums[st++] = nums[j++];
}
}
while (i <= mid) {
counts[src_idxs[i]] += j - mid - 1;
sorted_idxs[st] = src_idxs[i];
sorted_nums[st++] = nums[i++];
}
while (j <= right) {
sorted_idxs[st] = src_idxs[j];
sorted_nums[st++] = nums[j++];
}
for (int i = 0; i < right-left+1; ++i) {
src_idxs[left+i] = sorted_idxs[i];
nums[left+i] = sorted_nums[i];
}
}
void MergeSort(vector<int>& nums, int left, int right) {
int mid = left + (right - left) / 2;
if (left < right) {
MergeSort(nums, left, mid);
MergeSort(nums, mid+1, right);
MergeArray(nums, left, mid, right);
}
}
vector<int> countSmaller(vector<int>& nums) {
sorted_nums.reserve(nums.size());
sorted_idxs.reserve(nums.size());
counts = vector<int>(nums.size(), 0);
for (int i = 0; i < nums.size(); ++i) {
src_idxs.push_back(i);
}
MergeSort(nums, 0, nums.size()-1);
return counts;
}
};
4. 解题思路二
假设数据依然为 [ 11 , 8 , 3 , 9 , 7 , 1 , 2 , 5 ] [11, 8, 3, 9, 7, 1, 2, 5] [11,8,3,9,7,1,2,5],同时我们准备了 8 8 8 个桶来分别放置每个元素,然后我们从后往前开始遍历元素并将它们放入对应的桶内。当放置到元素 7 7 7 时,前面四个桶内的元素个数也就是右侧小于 7 7 7 的元素个数。
但是,如果我们计算右侧小于 7 7 7 的元素个数时要对前 4 4 4 个桶求和,而计算右侧小于 11 11 11 的元素个数时要对前 7 7 7 个桶求和,那么这时候的算法复杂度是 O ( n 2 ) O(n^2) O(n2),就和暴力求解法没有区别了。
所以,如果我们寻找到一种能在 O ( l o g n ) O(logn) O(logn) 复杂度下计算出前 n n n 个桶的和的算法,那么总的时间复杂度就变成了 O ( n l o g n ) O(nlogn) O(nlogn),问题也就迎刃而解了 。
这时候,我们只需要借助于一种数据结构——树状数组即可。
上图中的
a
[
1
]
−
a
[
8
]
a[1]-a[8]
a[1]−a[8] 就代表我们上面说的每个桶里面的元素个数,然后数组
c
c
c 有:
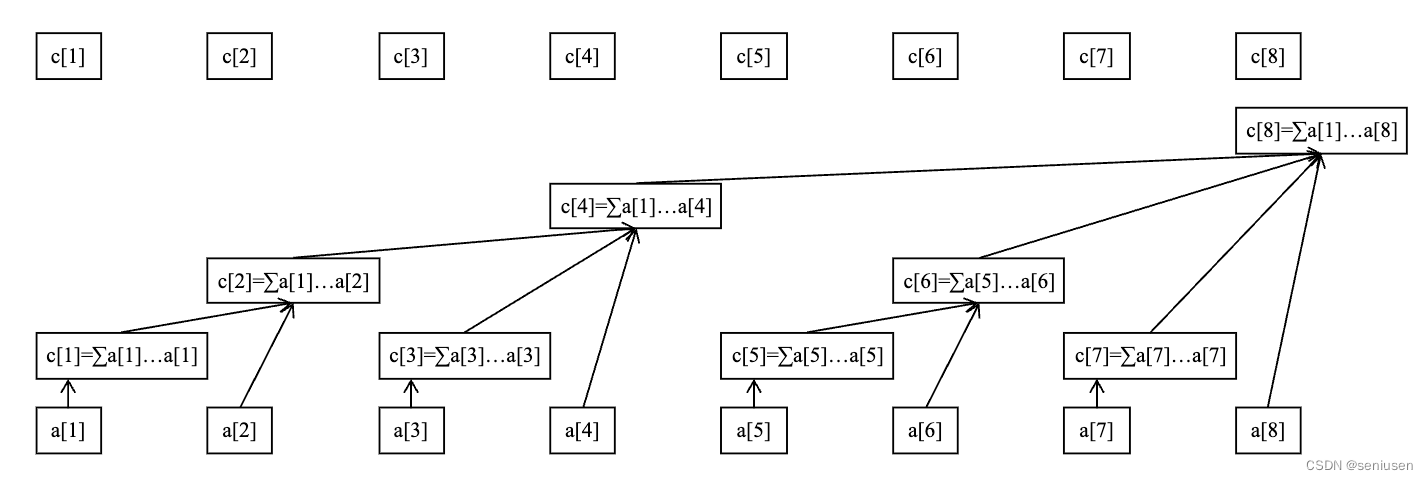
c [ 1 ] = a [ 1 ] c [ 2 ] = a [ 1 ] + a [ 2 ] c [ 3 ] = a [ 3 ] c [ 4 ] = a [ 1 ] + a [ 2 ] + a [ 3 ] + a [ 4 ] c [ 5 ] = a [ 5 ] c [ 6 ] = a [ 5 ] + a [ 6 ] c [ 7 ] = a [ 7 ] c [ 8 ] = a [ 1 ] + a [ 2 ] + a [ 3 ] + a [ 4 ] + a [ 5 ] + a [ 6 ] + a [ 7 ] + a [ 8 ] \begin{gather*} c[1] &=& a[1] \\ c[2] &=& a[1]+a[2] \\ c[3]&=&a[3] \\ c[4]&=&a[1]+a[2]+a[3]+a[4] \\ c[5]&=&a[5] \\ c[6]&=&a[5]+a[6] \\ c[7]&=&a[7] \\ c[8]&=&a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8] \\ \end{gather*} c[1]c[2]c[3]c[4]c[5]c[6]c[7]c[8]========a[1]a[1]+a[2]a[3]a[1]+a[2]+a[3]+a[4]a[5]a[5]+a[6]a[7]a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]
这样,比如我们要求前 5 5 5 个桶内的和时,只需要求 c [ 4 ] + c [ 5 ] c[4]+c[5] c[4]+c[5] 即可;求前 7 7 7 个桶内的和时,只需要求 c [ 4 ] + c [ 6 ] + c [ 7 ] c[4]+c[6]+c[7] c[4]+c[6]+c[7] 即可。
而当某个桶内元素增加的时候,我们需要同步更新对应的数组 c c c。比如,第二个桶内元素也即 a [ 2 ] a[2] a[2] 更新的时候, c [ 2 ] , c [ 4 ] , c [ 8 ] c[2], c[4], c[8] c[2],c[4],c[8] 都需要同步进行更新。
c [ k ] c[k] c[k] 管理的元素个数为区间 a [ k − l o w b i t ( k ) + 1 , k ] a[k-lowbit(k)+1, k] a[k−lowbit(k)+1,k],其中 l o w b i t ( k ) lowbit(k) lowbit(k) 代表 k k k 的二级制中从最低位的一个 1 1 1 开始的后面所有位所表示的数字。比如, 3 3 3 的二进制为 011 011 011,最低位的一个 1 1 1 在倒数第一位,所以 l o w b i t ( 1 ) = 1 lowbit(1)=1 lowbit(1)=1, c [ 3 ] c[3] c[3] 管理的元素个数为区间 a [ 3 , 3 ] a[3, 3] a[3,3]。 6 6 6 的二进制为 110 110 110,最低位的一个 1 1 1 在倒数第二位,所以 l o w b i t ( 6 ) = 1 0 2 进制 = 2 lowbit(6)=10_{2进制}=2 lowbit(6)=102进制=2, c [ 6 ] c[6] c[6] 管理的元素个数为区间 a [ 5 , 6 ] a[5, 6] a[5,6]。 8 8 8 的二进制为 1000 1000 1000,最低位的一个 1 1 1 在倒数第四位,所以 l o w b i t ( 8 ) = 100 0 2 进制 = 8 lowbit(8)=1000_{2进制}=8 lowbit(8)=10002进制=8, c [ 8 ] c[8] c[8] 管理的元素个数为区间 a [ 1 , 8 ] a[1, 8] a[1,8]。
求和过程:
-
所以,如果我们要求前 k k k 个元素的和时,第一步我们先拿到 c [ k ] c[k] c[k] 也即是 a [ k − l o w b i t ( k ) + 1 , k ] a[k-lowbit(k)+1, k] a[k−lowbit(k)+1,k] 的和。
-
下一步我们跳到 k 1 = k − l o w b i t ( k ) k_1=k-lowbit(k) k1=k−lowbit(k),这时候我们可以拿到 c [ k 1 ] c[k_1] c[k1] 也即是 a [ k 1 − l o w b i t ( k 1 ) + 1 , k − l o w b i t ( k ) ] a[k_1-lowbit(k_1)+1, k-lowbit(k)] a[k1−lowbit(k1)+1,k−lowbit(k)] 的和。
-
依次往下,直到最后一个区间的左边界为 1 1 1,我们可以拿到 c [ k n − 1 ] c[k_{n-1}] c[kn−1] 也即是 a [ 1 , k n − 1 ] a[1, k_{n-1}] a[1,kn−1] 的和。
-
再往下就到了第零个元素,循环结束,我们也就得到了前 k k k 个元素的和。
同理,某一个 a [ k ] a[k] a[k] 更新的时候,我们需要找到所有管理区间包含 a [ k ] a[k] a[k] 的 c c c 进行更新。
更新过程:
- 首先, c [ k ] c[k] c[k] 管理的元素个数为区间 a [ k − l o w b i t ( k ) + 1 , k ] a[k-lowbit(k)+1, k] a[k−lowbit(k)+1,k],所以,我们第一个先更新 c [ k ] c[k] c[k]。
- 然后,跳到 k 1 = k + l o w b i t ( k ) k_1=k+lowbit(k) k1=k+lowbit(k),更新 c [ k 1 ] c[k_1] c[k1],其中, c ( k , k + l o w b i t ( k ) ) c(k, k+lowbit(k)) c(k,k+lowbit(k)) 都不包含 a [ k ] a[k] a[k],具体证明可参考树状数组中的性质3 ;
- 依次往上,直到 k n − 1 k_{n-1} kn−1 大于数组 a a a 的大小,我们停止更新。
那么,现在还有最后一个问题,怎么求 l o w b i t ( k ) lowbit(k) lowbit(k) 呢?
负数的补码等于其对应的正数,符号位取反,其余位取反再加 1 1 1。
k
=
0
…
…
⏞
任意个
0
,
1
1
…
…
⏞
任意个
0
k = 0\overbrace{……}^{任意个0,1}1\overbrace{……}^{任意个0}
k=0……
任意个0,11……
任意个0
−
k
=
1
…
…
⏞
x
的对应位取反
1
…
…
⏞
任意个
1
-k = 1\overbrace{……}^{x的对应位取反}1\overbrace{……}^{任意个1}
−k=1……
x的对应位取反1……
任意个1
k
&
(
−
k
)
=
…
…
⏞
任意个
0
1
…
…
⏞
任意个
0
k \& (-k) = \overbrace{……}^{任意个0}1\overbrace{……}^{任意个0}
k&(−k)=……
任意个01……
任意个0
所以,正数与相反数按位取反就正好得到了我们想要的 l o w b i t ( k ) lowbit(k) lowbit(k),完美!
5. 代码实现二
class Solution {
public:
vector<int> c;
int lowbit(int k) {
return k & (-k);
}
void update(int k, int n) {
while (k < n) {
c[k] += 1;
k += lowbit(k);
}
}
int query(int k) {
int sum = 0;
while (k > 0) {
sum += c[k];
k -= lowbit(k);
}
return sum;
}
vector<int> countSmaller(vector<int>& nums) {
// 排序,去重,看看需要几个桶
vector<int> bucket = nums;
sort(bucket.begin(), bucket.end());
bucket.erase(unique(bucket.begin(), bucket.end()), bucket.end());
// 初始化树状数组,第0个位置不使用
c = vector<int>(bucket.size()+1, 0);
int n = c.size();
vector<int> counts(nums.size(), 0);
// 从后往前把每个元素放入桶内
for (int i = int(nums.size())-1; i >= 0; --i) {
// 当前元素应该放进哪个桶内,第0个桶对应a[1]
int idx = lower_bound(bucket.begin(), bucket.end(), nums[i]) - bucket.begin() + 1;
cout << nums[i] << ", " << idx << endl;
// 求前idx-1个桶的元素和
counts[i] = query(idx-1);
// 更新c
update(idx, n);
}
return counts;
}
};