目录
数字和
数字和介绍
数字和简单应用
哈沙德数
最小元素各数位之和
数字根
数字根介绍
数字根简单应用
数字和
数字和介绍
简单来说,数字和即一个整数数字每一位数值相加求和所得的值,数字和可以为任意正整数,使用代码获取一个数值的数字和模版如下:
while (num)
{
sum += num % 10;// 记录各位之和
num /= 10; // 获取下一个高位数值
}数字和简单应用
哈沙德数
题目链接:3099. 哈沙德数 - 力扣(LeetCode)
如果一个整数能够被其各个数位上的数字之和整除,则称之为 哈沙德数(Harshad number)。给你一个整数x。如果x是 哈沙德数 ,则返回x各个数位上的数字之和,否则,返回-1。
思路解析:
题目要求获取哈沙德数,根据题目描述,所谓哈沙德数即为当前数值可以被其数字和整除,所以直接使用数字和模版先获取数字和,再判断是否可以整除从而判断x是否为哈沙德数
参考代码:
/*
* @lc app=leetcode.cn id=3099 lang=cpp
*
* [3099] 哈沙德数
*/
// @lc code=start
class Solution
{
public:
int sumOfTheDigitsOfHarshadNumber(int x)
{
// 求各位之和
int sum = 0;
int tmp = x;
while (tmp)
{
sum += tmp % 10;
tmp /= 10;
}
if (x % sum == 0)
{
return sum;
}
return -1;
}
};
// @lc code=end最小元素各数位之和
题目链接:1085. 最小元素各数位之和 - 力扣(LeetCode)
给你一个正整数的数组A。
然后计算S,使其等于数组A当中最小的那个元素各个数位上数字之和。
最后,假如S所得计算结果是 奇数 ,返回 0 ;否则请返回 1。
思路解析:
本题只需要先获取数组中最小的数值,再求该数值的数字和即可
参考代码:
/*
* @lc app=leetcode.cn id=1085 lang=c
*
* [965] 最小元素各数位之和
*/
// @lc code=start
class Solution {
public:
int sumOfDigits(vector<int>& nums) {
int ret = *min_element(nums.begin(), nums.end());
int ans = 0;
while (ret){
ans += ret % 10;
ret /= 10;
}
if(ans % 2){
return 0;
}
return 1;
}
};
// @lc code=end数字根
数字根介绍
相比较于数字和来说,数字根是数值的每一位相加求和直到和结果为1位数,例如6278的数字根计算方式为6+2+7+8=23->2+3=5,所以6278的数字根为5
求一个数值的数字根有两种方法
- 循环求和
while (tmp > 9)
{
// 获取最低位和
while (tmp)
{
sum += tmp % 10;
tmp /= 10;
}
tmp = sum;
sum = 0;
}
sum = tmp;- 数学计算(去9法)
观察到因为数字根最大不会超过9,而对于十进制数值来说,例如6278,可以转化为6000+200+70+8,即6*1000+2*100+7*10+8*1

此时将上式转化为6*(999+1)+2*(99+1)+7*(9+1)+8,化简可得6*999+2*99+7*9+6+2+7+8,可以看到最后的6,2,7和8即为6278的每一位数值,而对于6+2+7+8=23来说可以划分为2*10+3*1,转化为2*(9+1)+3=2*9+2+3,可以看到最后的2和3即为23的每一位数值
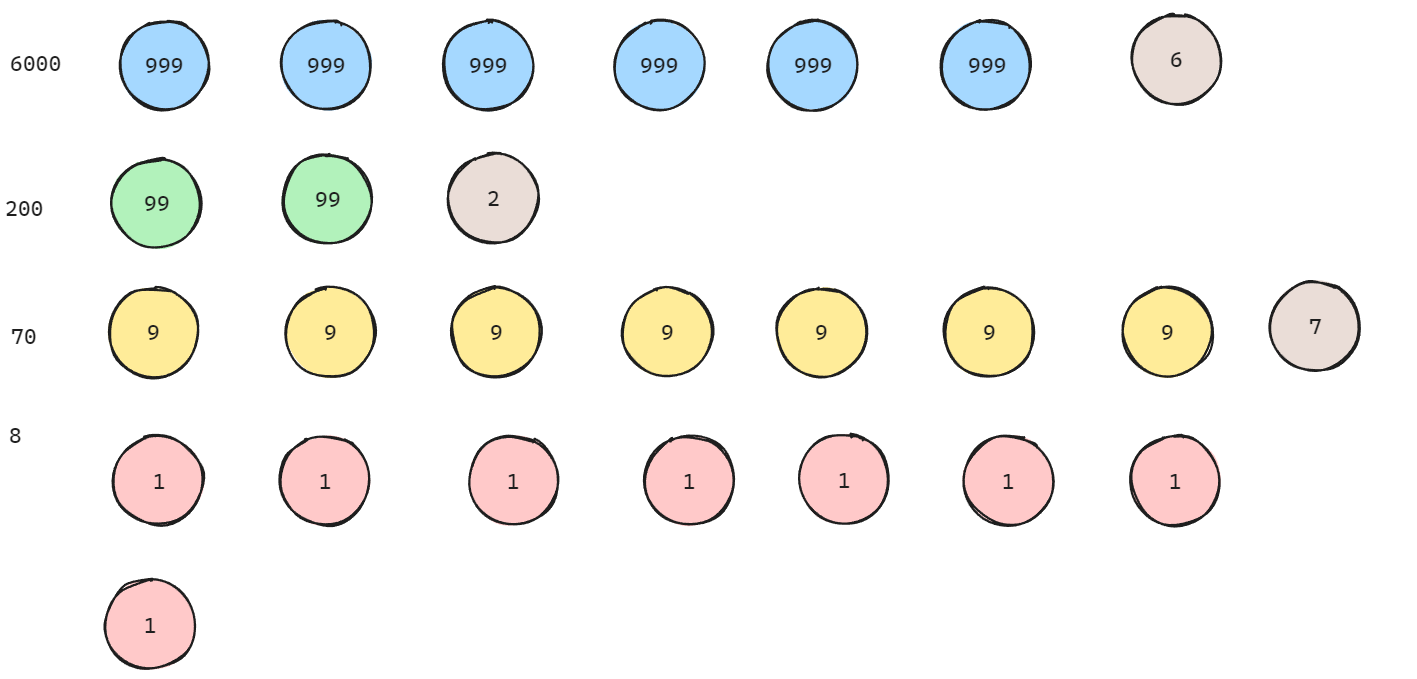
现在将范围扩大到所有十进制以内整数num,对于num来说,用i代表最低位位权值0,n-1代表最高位位权值,则上面等式可以写为通式:
转化为
此时算式中的即为每一次求和的数字和,多次求和直到和小于10,则和即为该数的数字根
而因为i为0时,是9的倍数,i为1时,
依旧是9的倍数。而去掉的每一部分,例如上面的6278中的6,2,7和8之和取9的余数此时和原数6278取9的余数相同(也称模9同余),有下面的结果:6278/9=698…5 ,所以6278%9=5
23 % 9 = 5,此时5即6278的数字根
但是如果该数值为9的倍数,那么余数为0,但是数字根不为0,所以此时需要改变计算方法
例如对于数值18来说,18%9=0,1+8=9,此时数字根并不等于余数,但是17%9=8,而17比18只少一个最低位,所以可以采取(18-1)%9+1=9,此时数字根等于余数
对于其余正常数值来说,也并不影响余数即为数字根,因为改变的都只是最低位的数值,而最低位数值都是1的倍数,所以相当于缺一个1补一个1
所以数字根,可以理解为数字相对于数值9来说的余数
综上所述,可以将代码简化为
(num-1)%9+1数字根简单应用
题目链接:258. 各位相加 - 力扣(LeetCode)
给定一个非负整数
num,反复将各个位上的数字相加,直到结果为一位数。返回这个结果。
思路解析:
数字根基本计算
参考代码:
/*
* @lc app=leetcode.cn id=258 lang=cpp
*
* [258] 各位相加
*/
// @lc code=start
class Solution
{
public:
int addDigits(int num)
{
return (num - 1) % 9 + 1;
}
};
// @lc code=end