variance和bias
MSE之前,先看两个更为朴素的指标:variance和bias。
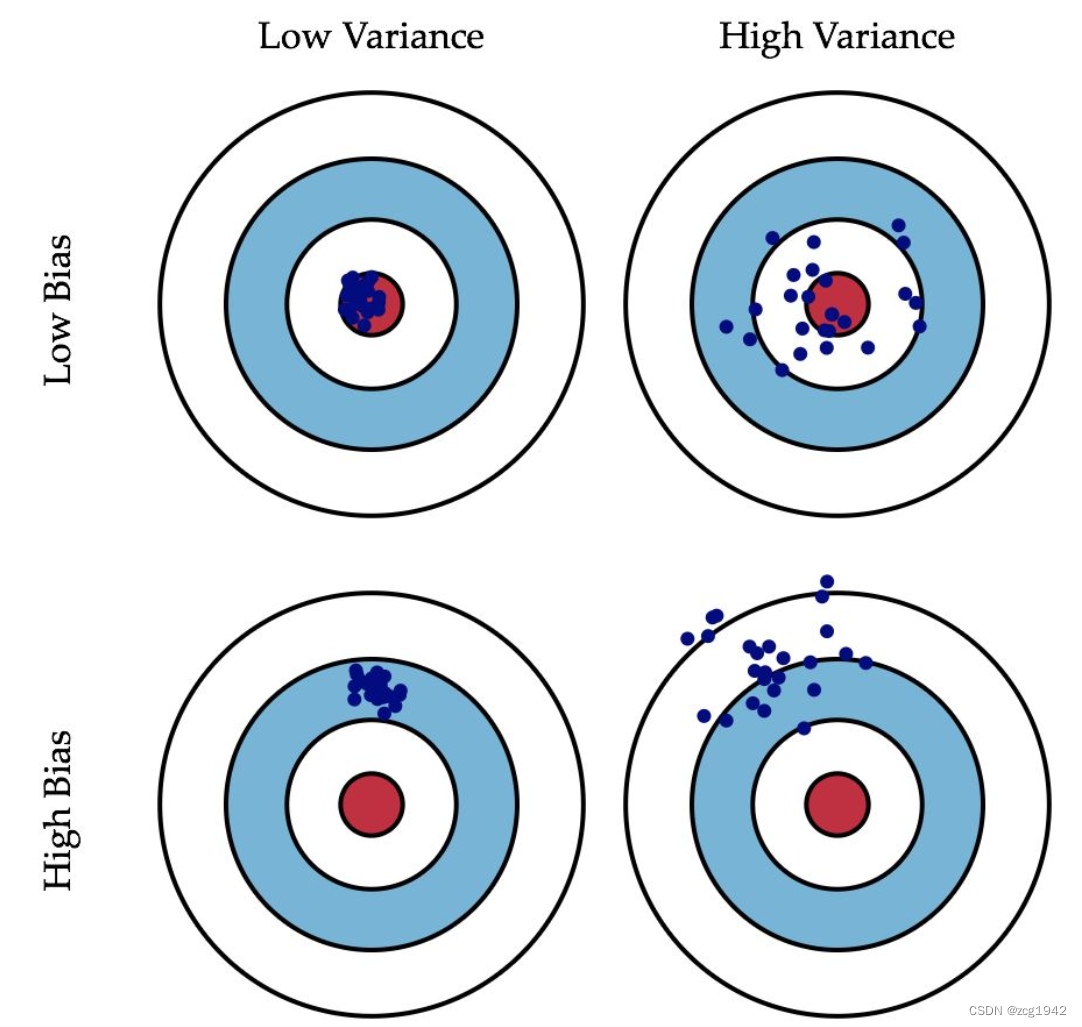
在打靶中,有的人所有的子弹都离靶心很远,偏差显然过高,但是很稳定地维持在某一点附近;有的人平均环数更高,但是分布太过分散。我们当然希望又准确又稳定,如何衡量二者呢?
MSE(Mean squared error)
可以发现,MSE正好是偏差和方差构成的:
方差公式:
V(X) = E[(X - E(X))²]
= E[X² - 2 X E(X) + E(X)²]
= E(X²) - 2 E(X) E(X) + [E(X)]²
= E[(X )²] - [E(X)]²
V(θhat -θ) = E[(θhat - θ)²] - [E(θhat - θ)]²,方差平移不变,所以:
V(θhat) = E[(θhat - θ)²] - [E(θhat) - E(θ)]²,等式变换:
E[(θhat - θ)²] = [E(θhat) - θ]² + V(θhat)=[Bias]² + V(θhat) = Bias² + Variance=MSE
对于网络模型的训练,由模型简单到复杂的过程中,欠拟合逐渐变为过拟合。因为随着模型变大,网络学习能力变强,偏差变小,但是受噪声影响变大,方差变大:

MSE和L2正则的关系?
在之前的文章中,我们看到L2正则和先验概率有一些联系,那么MSE怎么从贝叶斯的角度理解呢?
正则的本质是依据于先验概率,对参数进行约束,相当于参数有一个初始分布,最终估计出的不应该偏离这个值太远。
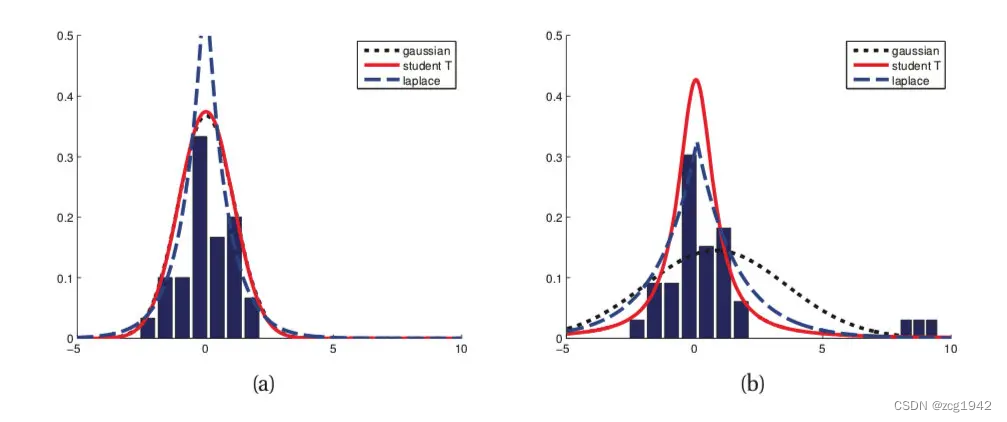
MSE衡量的是预测值与真实值之间的关系,那么关于预测值的似然函数可以写成关于GT的函数,如果这个函数是高斯分布,根据最大似然估计就可以得到MSE。所以MSE是先验为高斯分布下的最大似然估计。
机器学习常用损失函数小结 - 知乎
从收敛速度看MSE
MSE形状是开口向上的二次曲线,光滑连续、可导,便于使用梯度下降算法,是比较常用的一种损失函数。而且,MSE 随着误差的减小,梯度也在减小,即使固定学习因子,函数也能较快取得最小值。
因为是二次函数,当误差大于1时会被放大,小于1时会被减小。所以MSE会惩罚误差更大的点。
分类可以使用MSE吗
1. 直观地来说,分类中的label只是一个标签,和绝对数值大小没关系,所以强行拟合可能会有问题;
2. 刚才提到,MSE的先验是高斯分布,而分类和高斯分布关系不大,更像是伯努利分布;交叉熵则是以数据分布服从多项式分布为前提,所以分类更多使用交叉熵;
3.从梯度更新上看,MSE中的预测值是sigmoid后的输出,那么求导时就会出现sigmoid的导数,而sigmoid的导数在两侧很小,会导致梯度下降不了。比如真实值是1,不管预测是0还是1附近,梯度都很小。MSE在这里变成了非凸优化。
那么交叉熵就没有这个问题吗?还真没有,因为在求梯度过程中能消掉。可以看下面的回答:
交叉熵损失(Cross-Entropy)和平方损失(MSE)究竟有何区别? - 陆壹爵爷的文章 - 知乎
https://zhuanlan.zhihu.com/p/423179343
回归一定使用MSE吗
在第一篇使用CNN做超分的SRCNN中,确实使用的还是MSE。但是正如前面提到的,MSE过分关注离群点,和人眼不太符合;同时MSE可能会损失高频细节,这和它高斯分布的假设也有关系。
所以超分,去噪更多使用L1,SSIM等,尤其后面又有GAN loss等的出现,MSE使用得更少了。
分类问题中为什么用交叉熵而不用MSE KL散度和交叉熵的关系_分类为什么用交叉熵不用mse-CSDN博客
交叉熵损失(Cross-Entropy)和平方损失(MSE)究竟有何区别? - 陆壹爵爷的文章 - 知乎
https://zhuanlan.zhihu.com/p/423179343
那么,交叉熵可以用于回归问题吗?有些情况下,还真可以:分类必然交叉熵,回归无脑MSE?未必 - 知乎
https://www.cnblogs.com/USTC-ZCC/p/13219281.htmlAI 面试高频问题: 为什么二分类不用 MSE 损失函数? - mathinside的个人空间 - OSCHINA - 中文开源技术交流社区
RMSE (Root Mean Square Error)
均方根误差RMSE就是对MSE开方之后的结果
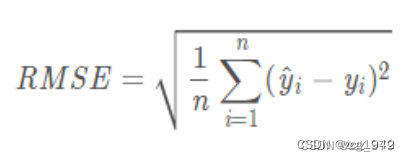
MAE(mean absolute error)
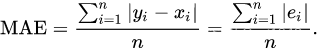
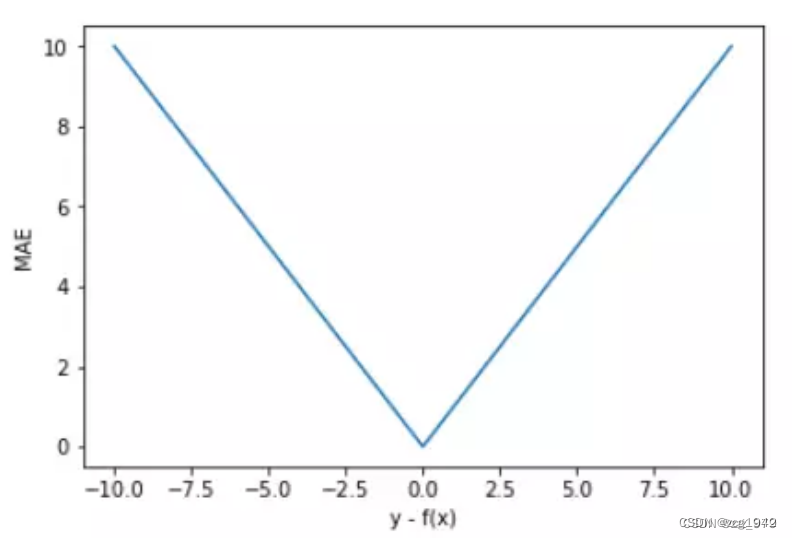
对外点更鲁棒:
mean absolute percentage error (MAPE)

where At is the actual value and Ft is the forecast value.
MAPE和MAE最大的区别就是进行了归一化。相当于在绝对误差的基础上又考虑了相对误差。
MAPE (Mean absolute percentage error)
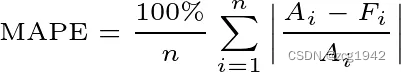
Symmetric mean absolute percentage error (SMAPE
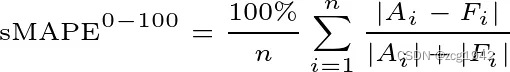
进一步在归一化的时候同时考虑了真实值和预测值。为什么同时考虑,是为了解决MAPE没有上限的问题:除以一个很小的值,结果会很大。
对于分母,为了避免真实值和预测值之和为负数,所以各自取了绝对值再求和。
有的公式分母会再除以2,这样SMAPE最大值就会达到2.

我们可以看到虽然0-200的范围不太常见,但它是更接近MAPE的:
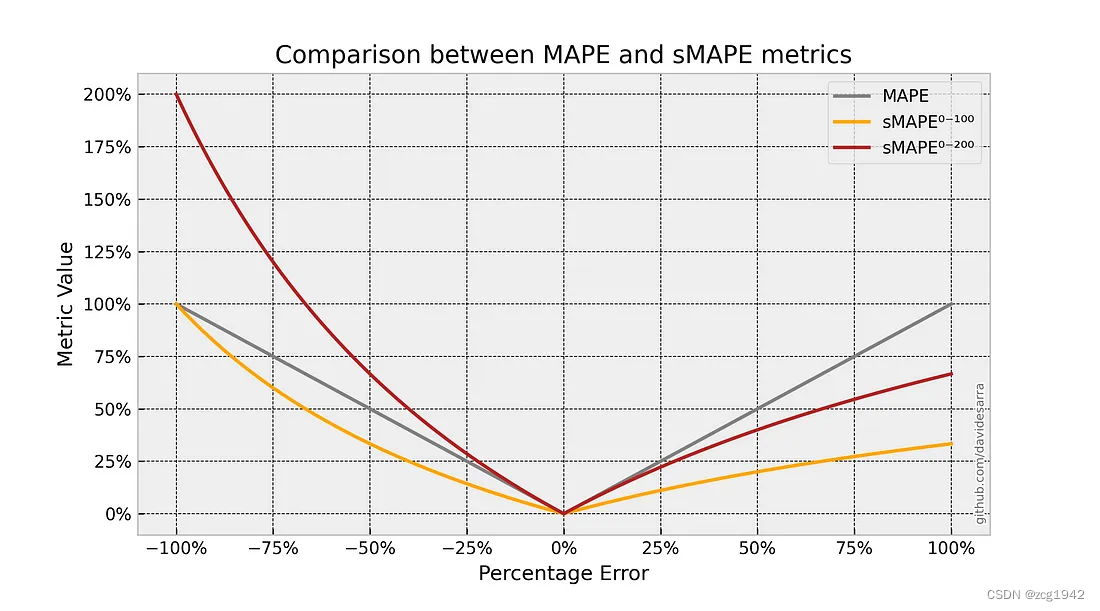
也可以看到两种sMAPE都不是对称的,0-200的甚至在左边大于MAPE,在右边小于MAPE。
没有达到”对称“的效果:
- Over-forecasting: At = 100 and Ft = 110 give SMAPE = 4.76%
- Under-forecasting: At = 100 and Ft = 90 give SMAPE = 5.26%.
反而是MSE和MAE有对称效果。
实验结果评估准则 - 知乎
通俗易懂方差(Variance)和偏差(Bias)_偏差和方差-CSDN博客深度学习常用损失MSE、RMSE、MAE和MAPE-CSDN博客
https://medium.com/@davide.sarra/how-to-interpret-smape-just-like-mape-bf799ba03bdc