0.概述

记录向量的元素访问、插入、区间删除、单元素删除、查找、唯一化、遍历算法。

1.元素访问

重载操作符"[]"，使元素访问更加便捷。

template <typename T> T & Vector<T>::operator[] ( Rank r ) //重载下标操作符
{ return _elem[r]; } // assert: 0 <= r < _size

template <typename T> const T & Vector<T>::operator[] ( Rank r ) const //仅限于做右值
{ return _elem[r]; } // assert: 0 <= r < _size

经重载后操作符“[]”返回的是对数组元素的引用，这就意味着它既可以取代get()操作（通常作为赋值表达式的右值），也可以取代set()操作（通常作为左值）。

2.置乱器

目标：借助操作符 “[]” 随机置乱向量，使各元素等概率出现于各位置。
策略：自后向前，依次将各元素与随机选取的某一前驱（含自身）做交换

template <typename T> void permute ( Vector<T>& V ) { //随机置乱向量，使各元素等概率出现于各位置
   for ( int i = V.size(); i > 0; i-- ) //自后向前
      swap ( V[i - 1], V[rand() % i] ); //V[i - 1]与V[0, i)中某一随机元素交换
}

从待置乱区间的末元素开始，逆序地向前逐一处理各元素。

注意，这里的交换操作swap()，隐含了三次基于重载操作符“[]”的赋值。

• 通过反复调用 permute()算法，可以生成向量 V[0, n)的所有 n!种排列。
• 由该算法生成的排列中，各元素处于任一位置的概率均为 1/n
• 该算法生成各排列的概率均为 1/n!

3.判等器与比较器

算法思想：

• 可比较或可比对的任何数据类型，而不必关心如何定义以及判定其大小或相等关系。
• 将比对和比较操作的具体实现剥离出来，直接讨论算法流程本身。
• 在定义对应的数据类型时，通过重载"<“和”=="之类的操作符，给出大小和相等关系的具体定义及其判别方法。

template <typename T> static bool lt ( T* a, T* b ) { return lt ( *a, *b ); } //less than
template <typename T> static bool lt ( T& a, T& b ) { return a < b; } //less than
template <typename T> static bool eq ( T* a, T* b ) { return eq ( *a, *b ); } //equal
template <typename T> static bool eq ( T& a, T& b ) { return a == b; } //equal

在一些复杂的数据结构中，内部元素本身的类型可能就是指向其它对象的指针；而从外部更多关注的，则往往是其所指对象的大小。若不加处理而直接根据指针的数值（即被指对象的物理地址）进行比较，则所得结果将毫无意义。

4.无序查找

4.1 判等器

Vector::find(e)接口，功能语义为“查找与数据对象e相等的元素”。这同时也暗示着，向量元素可通过相互比对判等，但未必支持比较的向量，称作无序向量（unsorted vector）。

4.2 顺序查找

从末元素起自后向前，逐一取出各个元素并与目标元素e进行比对，直至发现与之相等者（查找成功），或者直至检查过所有元素之后仍未找到相等者（查找失败）。这种依次逐个比对的查找方式，称作顺序查找。

4.3 实现

template <typename T> //在无序向量中顺序查找e：成功则返回最靠后的出现位置，否则返回lo-1
Rank Vector<T>::find ( T const& e, Rank lo, Rank hi ) const { //0 <= lo < hi <= _size
   while ( ( lo < hi-- ) && ( e != _elem[hi] ) ); //从后向前，顺序查找
   return hi; //若hi < lo，则意味着失败；否则hi即命中元素的秩
}

细节：

• 当同时有多个命中元素时，统一约定返回其中秩最大者
• while循环的控制逻辑由两部分组成，首先判断是否已抵达lo，再判断当前元素与目标元素是否相等。得益于C/C++语言中逻辑表达式的短路求值特性，在前一判断非真后循环会立即终止，而不致因试图引用已越界的秩（-1）而出错。

4.4 复杂度

最坏情况 查找终止于首元素_elem[lo]，运行时间为O(hi - lo) = O(n)。
最好情况 查找命中于末元素_elem[hi - 1]，仅需O(1)时间。
对于规模相同、内部组成不同的输入，渐进运行时间却有本质区别，故此类算法也称作输入敏感的算法。

5. 插入

5.1 算法实现

算法思想：插入之前必须首先调用expand()算法，核对是否即将溢出。

template <typename T> //将e插入至[r]
Rank Vector<T>::insert ( Rank r, T const& e ) { //0 <= r <= size
   expand(); //如必要，先扩容
   for ( Rank i = _size; r < i; i-- ) //自后向前，后继元素
      _elem[i] = _elem[i-1]; //顺次后移一个单元
   _elem[r] = e; _size++; //置入新元素并更新容量
   return r; //返回秩
}

为保证数组元素物理地址连续的特性，随后需要将后缀_elem[r, _size)（如果非空）整体后移一个单元（图©）。这些后继元素自后向前的搬迁次序不能颠倒，否则会因元素被覆盖而造成数据丢失。在单元_elem[r]腾出之后，方可将待插入对象e置入其中（图(d)）。

5.2 复杂度分析

时间主要消耗于后继元素的后移，线性正比于后缀的长度，故总体为O(_size - r + 1)。
r取最大值_size时为最好情况，只需O(1)时间；r取最小值0时为最坏情况，需要O(_size)时间。

若插入位置等概率分布，则平均运行时间为O(_size) = O(n)

运行时间主要来自于后继元素顺次后移的操作。因此对于每个插入位置而言，对应的移动操作次数恰好等于其后继元素（包含自身）的数目。不难看出它们也构成一个等差数列（数学期望O($n^2$) m为后继元素数目），故在等概率的假设条件下，其均值（数学期望）应渐进地与其中的最高项同阶，为O(n)。

6. 删除

应将单元素删除视作区间删除的特例，并基于后者来实现前者。

6.1 区间删除

template <typename T> Rank Vector<T>::remove( Rank lo, Rank hi ) { //0 <= lo <= hi <= n
   if ( lo == hi ) return 0; //出于效率考虑，单独处理退化情况
   while ( hi < _size ) _elem[lo++] = _elem[hi++]; //后缀[hi, _size)顺次前移hi-lo位
   _size = lo; shrink(); //更新规模，lo=_size之后的内容无需清零；如必要，则缩容
   //若有必要，则缩容
   return hi - lo; //返回被删除元素的数目
}

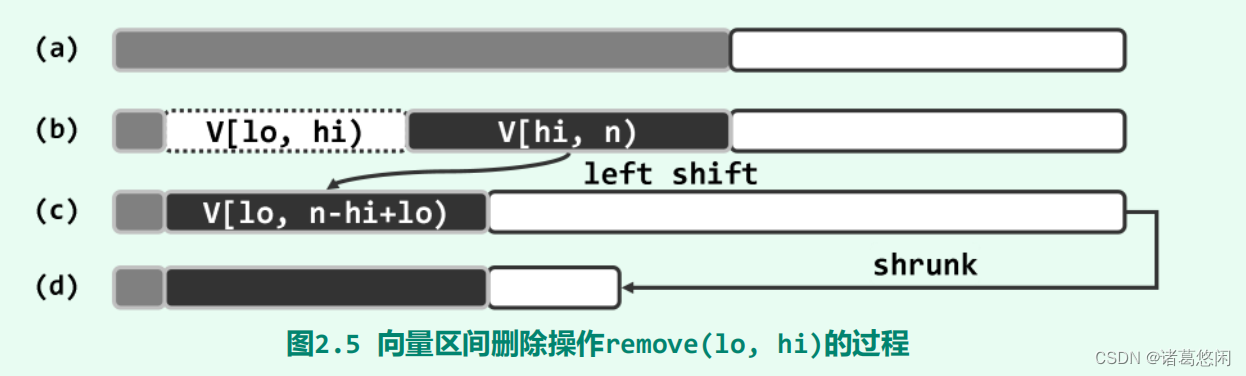
设[lo, hi)为向量（图(a)）的合法区间（图(b)），则其后缀[hi, n)需整体前移hi - lo个单元（图©）。与插入算法同理，后继元素自前向后的移动次序也不能颠倒。

• 若以自后向前得次序逐个前移后继元素，位置靠前的元素，可能被位置靠后（优先移动）的元素覆盖，从而造成数据的丢失。
  
  V.remove(0, 2)以删除其中的前两个元素，可见，原数据元素V[2] = 2并未顺利转移至输出向量中的V[0]，即出现数据的丢失现象。

6.2 单元删除

重载即可实现如下另一同名接口remove®。

template <typename T> T Vector<T>::remove( Rank r ) { //删除向量中秩为r的元素，0 <= r < size
   T e = _elem[r]; //备份被删除元素
   remove( r, r + 1 ); //调用区间删除算法，等效于对区间[r, r + 1)的删除
   return e; //返回被删除元素
}

6.3 复杂度

remove(lo, hi)的计算成本，主要消耗于后续元素的前移，线性正比于后缀的长度，总体不过O(m + 1) = O(_size - hi + 1)。
结论：

区间删除操作所需的时间，应该仅取决于后继元素的数目，而与被删除区间本身的宽度无关。

被删除元素在向量中的位置越靠后（前）所需时间越短（长），最好为O(1)，最坏为O(n) = O(_size)。

7. 唯一化

所谓向量的唯一化处理，就是剔除其中的重复元素。

7.1 实现

template <typename T> Rank Vector<T>::dedup() { //删除无序向量中重复元素（高效版）
   Rank oldSize = _size; //记录原规模
   for ( Rank i = 1; i < _size; ) //自前向后逐个考查_elem[1,_size)
      if ( -1 == find(_elem[i], 0, i) ) //在前缀[0,i)中寻找与[i]雷同者（至多一个），O(i)
         i++; //若无雷同，则继续考查其后继
      else
         remove(i); //否则删除[i]，O(_size-i)
   return oldSize - _size; //被删除元素总数
}

该算法自前向后逐一考查各元素_elem[i]，并通过调用find()接口，在其前缀中寻找与之雷同者。若找到，则随即删除；否则，转而考查当前元素的后继。

7.2 正确性

在while循环中，在当前元素的前缀_elem[0, i)内，所有元素彼此互异

7.3 复杂度

随着循环的不断进行，当前元素的后继持续地严格减少

这里所需的时间，主要消耗于find()和remove()两个接口。

find()时间应线性正比于查找区间的宽度，即前驱的总数；
remove()时间应线性正比于后继的总数。因此，每步迭代所需时间为O(n)，总体复杂度应为O($n^2$)。

8. 遍历

8.1 实现

算法思想：

1. 借助函数指针*visit()指定某一函数，该函数只有一个参数，其类型为对向量元素的引用，故通过该函数即可直接访问或修改向量元素。
2. 也可以函数对象的形式，指定具体的遍历操作。这类对象的操作符“()”经重载之后，在形式上等效于一个函数接口，故此得名。
   

template <typename T> void Vector<T>::traverse( void ( *visit )( T& ) ) //借助函数指针机制
{ for ( Rank i = 0; i < _size; i++ ) visit( _elem[i] ); } //遍历向量

template <typename T> template <typename VST> //元素类型、操作器
void Vector<T>::traverse( VST& visit ) //借助函数对象机制
{ for ( Rank i = 0; i < _size; i++ ) visit( _elem[i] ); } //遍历向量

相比较而言，后一形式的功能更强，适用范围更广。

比如，函数对象的形式支持对向量元素的关联修改。也就是说，对各元素的修改不仅可以相互独立地进行，也可以根据某个（些）元素的数值相应地修改另一元素。前一形式虽也可实现这类功能，但要繁琐很多。

例如：统一递增向量中的各元素

template <typename T> void increase ( Vector<T> & V ) //统一递增向量中的各元素
{  V.traverse ( Increase<T>() );  } //以Increase<T>()为基本操作进行遍历

8.2 复杂度

遍历操作本身只包含一层线性的循环迭代，故除了向量规模的因素之外，遍历所需时间应线性正比于所统一指定的基本操作所需的时间。故这一遍历的总体时间复杂度为O(n)。

9. 总结

1. 置乱算法 permute() 从待置乱区间的末元素开始，逆序地向前逐一处理各元素。时间复杂度为O(n)。
2. 顺序查找算法 find() 从末元素起自后向前，逐一取出各个元素并与目标元素进行比对，时间复杂度应线性正比于查找区间的宽度，即前驱的总数。
3. 插入算法insert() ，时间复杂度线性正比于后缀的长度为。
4. 删除算法remove() ，时间复杂度应该仅取决于后继元素的数目。
5. 唯一化算法deduplicate()，主要消耗于find()和remove()两个接口，时间复杂度O($n^2$)