堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏、最好、平均时间复杂度均为O(nlogn),是不稳定排序。
小根堆(最小堆):每个结点的值都<=其左右孩子结点的值。

大根堆:每个结点的值都>=其左右孩子结点的值。
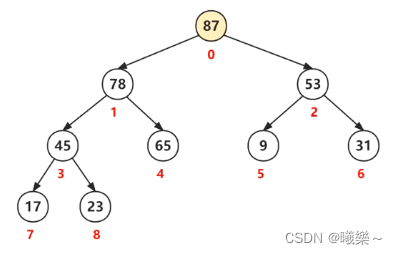
没有规定其左右孩子之间的大小关系,这与二叉排序树不同。
结点的编号:自顶向下,自左至右连续给结点编号0,1,2,…,n-1,之后按结点编号将树中各结点顺序的存放于顺序表中。

i = 0位置为根结点,没有双亲;i>0时,双亲结点为(i-1)/2;
若2*i+1<n,则i的左孩子为2*i+1;若2*i+2<n,则i的右孩子为2*i+2;
左孩子i都为奇数,右孩子i都为偶数;
i所在的层次为log2(i+1);
堆排序的降序排序
1.将待排序的序列构建成一个最小堆(先局部再整体从底向上)
整个序列的最小值为根节点的值

2.将根节点的值与末尾元素的值交换
3.剩余n-1个元素继续进行上述两步,直到只剩一个元素,排序完成
创建小根堆
使用tmp存根的值,i存根下标,j存其左子下标,先对比其左右两子的大小(如果存在),使j指向小的。
对比根和小的子孩子的值,如果根小则排列完成,否则交换根的小子的值,之后继续排后面的。
将tmp赋给nums[i],它应该在的地方
void FilterDown(int *nums,int start,int end)//start是当前根结点下标,end为当前小根堆结束下标
{
int i = start, j = i*2+1;
int tmp = nums[start];//保存根结点的值
while ( j<=end )
{
if(j+1<=end)//有左右两个孩子
j = nums[j] < nums[j+1] ? j : j+1;//j指向小的孩子
if (tmp < nums[j])
break;
else
nums[i] = nums[j];//小的存到上面
i = j;
j = i * 2 + 1;
}
nums[i] = tmp;
}堆排序
先将序列排序成最小堆,然后一个一个交换,存在数组末尾,直到所有数排完。
void HeapSort(int *nums,int n)
{
if (nums == nullptr || n < 2)return;
int pos = (n-2)/2;//当前小根堆的根结点下标
//调整成最小堆
while(pos>=0)
{
FilterDown(nums, pos, n-1);
pos--;//下一个根
}
//排序
int end = n-1;
while (end > 0)
{
swap(nums[0], nums[end]);//交换根与最后一个位置的值
end--;//规模缩小
FilterDown(nums, 0, end);
}
}堆排序的升序排序
升序排序是创建大根堆来排,其他根上面的代码一样。
创建堆也可以不用i,j两个存下标,下面用一个写大根堆(这是好久之前用C语言写的,有点不一样)
//创建大根堆
void CreateHeap(int* num, int index, int n)//index是下标,该下标的节点作为父节点
{
int t = num[index];//存一下父节点的值
int i = index * 2;//i指向其左子孩子下标(如果存在的话)
while (i <= n)//有孩子
{
if (i < n)//有两个孩子
{
if (num[i] < num[i + 1])//找大的孩子
i++;
}
if (t >= num[i])//如果根节点最大,就创建好了当前大根堆,出循环
break;
else//如果不是,则把最大的孩子放父节点
{
num[i / 2] = num[i];
i *= 2;//i指向这个最大值孩子节点的左孩子
}
}
num[i / 2] = t;//把刚开始的父节点值存在排好的大根堆的父节点
}
void HeapSort(int* num, int n)
{
int i;
for (i = n / 2; i >= 1; i--)//创建大根堆
CreateHeap(num, i, n);
for (i = n; i >= 1; i--)//大根堆的顶(最大的值)与大根堆最后一个值交换(排序放在数组的最后一个)
{
int t = num[1];
num[1] = num[i];
num[i] = t;
CreateHeap(num, 1, i - 1);//排好一个所以i-1,顶上的根改变了,所以从1开始再一次排好大根堆
}
}