二叉树

如下图，是一个二叉树的结构图片：

 

可以看到无论是对象“9”、还是“5”、“13”、“2”、“7”、“11”、“15”它们的下面分别都叉了两个其他的对象。而且这两个对象都是左边的数值要小一些，右边的数值要大一些。

所以这就是二叉树的结构特点：

1、每个对象（节点）下面最多拥有两个对象（节点）（标准说法则是：非叶子节点最多拥有两个子节点，叶子节点则是“1”、“3”、“6”、“8”、“11”、“14”、“16”这些节点。）。

2、小对象均在二叉树的左边，大对象均在二叉树的右边。（标准说法是：非叶子节点值大于左边子节点、小于右边子节点。）

3、没有值相等重复的节点。

为什么会有树这种数据结构？

原因是为了提高查询效率

树的数据结构的特点：

1、查询效率高。

2、插入效率慢（因为树的结构特点都是小对象在左边，大对象在右边，这样的话每次插入新的对象都会根据实际情况来调整每个对象的位置，所以说插入效率会很慢。）

平衡二叉树

平衡二叉树它基于二叉树，它的结构和二叉树一样。

但是二叉树会出现下图这种情况（只有一个根节点）：

 

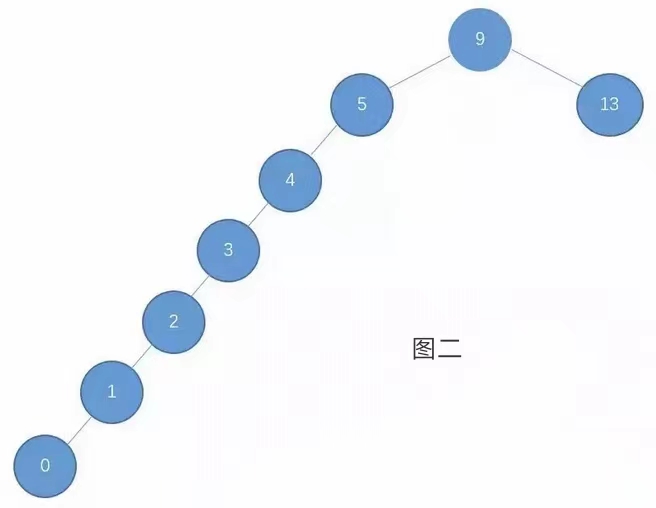
这种情况它会降低对象的查询效率。

假如说我们要查询对象“1”：

用图一的树状图来查询：从“9”到“5”查询一次（查询次数为1），从“5”到“2”再查询一次（查询次数为2），从“2”到“1”再查询一次（查询次数为3）。总计查询了3次。

用图二的树状图来查询：从“9”到“5”查询一次（查询次数为1），从“5”到“4”再查询一次（查询次数为2），从“4”到“3”再查询一次（查询次数为3），从“3”到“2”再查询一次（查询次数为4），从“2”到“1”再查询一次（查询次数为5）。总计查询了5次。

所以说图二的出现就会降低二叉树的查询效率。

而平衡二叉树则没有图二这种情况。其余特点和二叉树一样。

红黑树

如下图，就是红黑树：

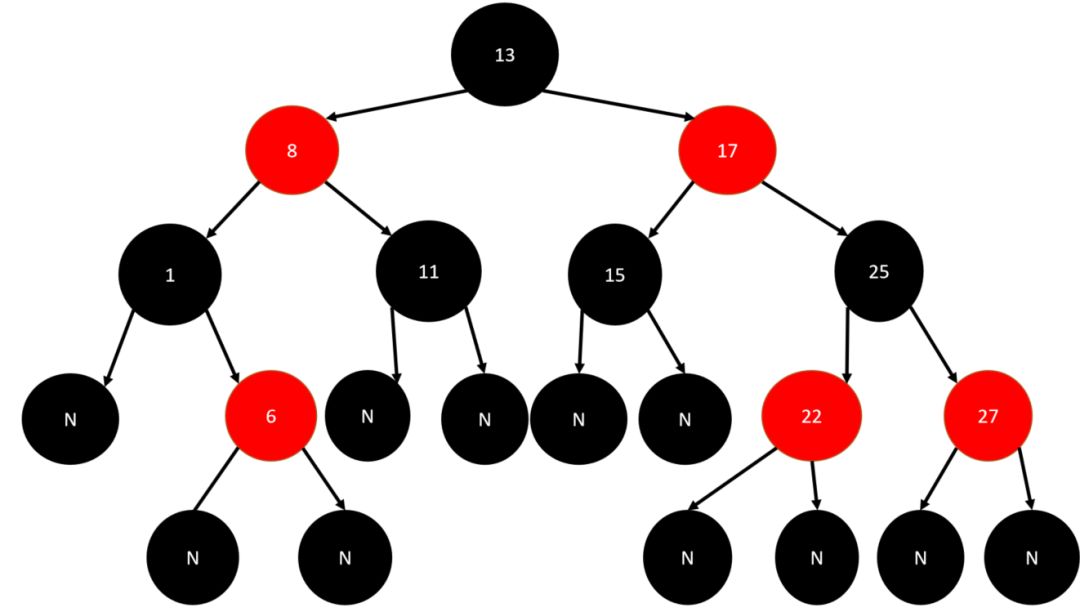
可以发现红黑树的每个节点非黑即红。再仔细观察，可以发现它只有根节点才是黑色的。而且可以看到红色节点下面的子节点都是黑色的。

所以说红黑树的结构特点大致可以总结为：

1、每个节点非黑即红。

2、根节点总是黑色的。

3、如果节点是红色的，则它的子节点必须是黑色的。

4、非叶子节点值大于左边子节点、小于右边子节点。

那么为什么会有红黑树呢？

树的查询效率高、插入效率慢。

平衡二叉树追求绝对平衡。它只适用于查询，并不适合插入。

红黑树追求相对平衡。它不仅仅适用查询，也适用插入（但是“查询效率高、插入效率慢”的本质还是存在的。）。

B树

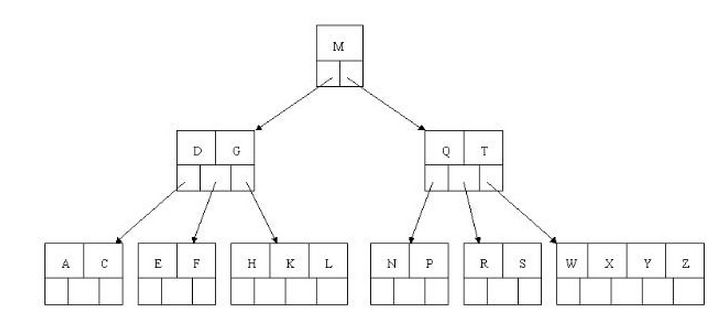
上图就是B树。

能看到B树的每个节点有多个对象。再仔细看，B树的高度矮一些。正是因为B树的高度要矮一些，所以说B树的查询效率也会更高一些。

总结：

1、B树的查询效率要高一些，主要是因为B树的高度相对矮一些。

2、B树的节点可以存多个对象。

3、非叶子节点值大于左边子节点、小于右边子节点。

B+树

这是B+树的图示。Mysql索引就是通过B+树来实现的。

B+树它和B树一样树的高度都不高，而且每个节点都可以存储多个对象。区别就是它的叶子节点（也就是最下面的一排Q）会形成一个单向链表，因此它的范围查找速度是很高的。

所以相对于B树而言，B+树很大的提高了范围查找的速度。

B*树

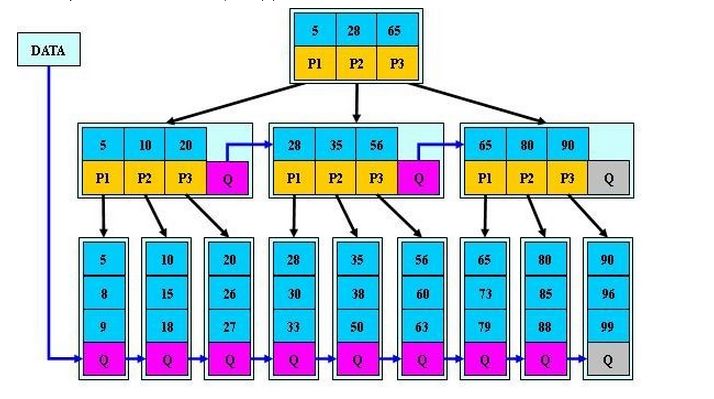
B*树和B+树十分相似，B*树除了叶子节点以外，它的非叶子节点也会形成一个链表。

B*树节点满时会检查兄弟节点是否满（因为每个节点都有指向兄弟的指针），如果兄弟节点未满则向兄弟节点转移对象，如果兄弟节点已满，则从当前节点和兄弟节点各拿出三分之一的数据创建一个新的节点出来。

因此，B*树除了具备B+树的特征以外，还令节点的空间使用率变的更高。