题干

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

解题思路

从楼底到楼顶共有n阶楼梯，我们要求爬n阶楼梯有几种方法，我们思考n阶楼梯可以从第几阶楼梯爬来，根据我们每次可以爬1或2个台阶，可得n阶楼梯是由第n-1阶台阶走一个，或第n-2阶台阶走两个到达。因此爬n阶楼梯的方法数其实是爬n-1阶楼梯的方法数加爬n-2阶楼梯的方法数。用dp数组可以记录每一阶楼梯的方法数。

动态规划五部曲

1.确定dp数组以及下标的含义

dp[i]：爬到 i 阶楼梯有dp[i]种方法

2.确定递推公式

dp[i] = dp[i-1] + dp[i-2]

3.dp数组如何初始化

dp[1] = 1 dp[2] = 2

需要注意的是：题目中说了n是一个正整数，题目根本就没说n有为0的情况。

所以我们可以不用讨论dp[0]的初始化，只初始化dp[1] = 1，dp[2] = 2，然后从i = 3开始递推，这样才符合dp[i]的定义。

4.确定遍历顺序

从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，遍历顺序一定是从前向后遍历的

5.举例推导dp数组

举例当n为5的时候，dp table（dp数组）应该是这样的

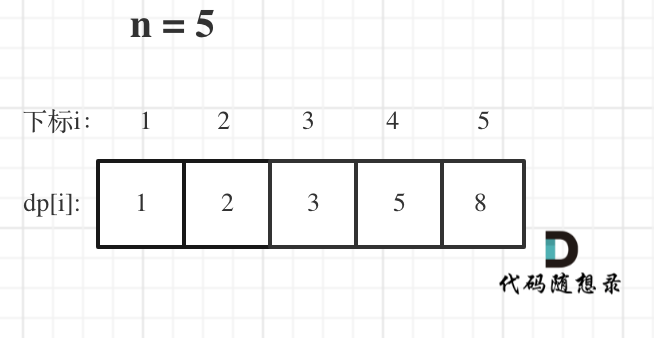
如果代码出问题了，就把dp table 打印出来，看看究竟是不是和自己推导的一样。

其实我们可以发现这道题目其实就是斐波那契数列，只不过题目中没有给出明显的递推公式，导致本题增加了难度。

完整代码如下：

class Solution {
public:
    int climbStairs(int n) {
        if(n < 3)
        return n;
        //初始化dp数组
        int dp[n+1];
        dp[1] = 1;
        dp[2] = 2;
        for(int i = 3; i <=n; i++){
            dp[i] = dp[i-1] + dp[i-2];
        }
    return dp[n];
    }
};