1 Title
Diffusion Improves Graph Learning(Johannes Gasteiger, Stefan Weißenberger, Stephan Günnemann)【NeurIPS 2019】
2 Conclusion
This study removes the restriction of using only the direct neighbors by introducing a
powerful, yet spatially localized graph convolution: Graph diffusion convolution(GDC). GDC leverages generalized graph diffusion, examples of which are the heat kernel and personalized PageRank. It alleviates the problem of noisy and often arbitrarily defined edges in real graphs. GDC is also closely related to spectral-based models and thus combines the strengths of both spatial (message passing) and spectral methods.
3 Good Sentences
1、Message Passing Neural Networks (MPNNs) are the prevalent approach in this field but they only pass messages between neighboring nodes in each layer. These messages are then aggregated at each node to form the embedding for the next layer. While MPNNs do leverage higher-order neighborhoods in deeper layers, limiting each layer’s messages to one-hop neighbors seems arbitrary.(The shortcomings of previous GNNs method)
2、To reconcile these two separate approaches and combine their strengths we propose
a novel technique of performing message passing inspired by spectral methods: Graph diffusion
convolution (GDC). Instead of aggregating information only from the first-hop neighbors, GDC
aggregates information from a larger neighborhood. This neighborhood is constructed via a new
graph generated by sparsifying a generalized form of graph diffusion.since GDC generates a new
sparse graph it is not limited to MPNNs and can trivially be combined with any existing graph-based model or algorithm in a plug-and-play manner(The motivation and advantages of GDC)
3、While there are tight connections between GDC and spectralbased models, GDC is actually spatial-based and therefore does not share their limitations. Similar to polynomial filters, GDC does not compute an expensive eigenvalue decomposition, preserves locality on the graph and is not limited to a single graph after training(The improvement of GDC when compared with spatial-based works)
GDC说白了就是个预处理步骤,通过扩散步骤,把原图生成出一个稠密图,然后用PPR或者热核等方法中的某一个把图在稀疏化,最后把稀疏图投入一种图算法。但是GDC利用了图的节点同质性,所以适用度有限。
通过引入一个强大的、空间局部化的图形卷积:图形扩散卷积(GDC ),消除了只使用直接邻居的限制。用图扩散卷积代替消息传递,在监督和非监督任务以及各种数据集上,在广泛的模型中有显著的性能改进。此外,GDC不限于GNNs,而是可以与任何基于图的模型或算法(例如谱聚类)相结合,而不需要对后者进行任何改变或也不影响其计算复杂度。
GDC利用了广义图扩散。
广义图扩散:
假设有无向图G =(V,E),其节点集为V,边集为E .用 N = |V|表示节点数,A∈表示邻接矩阵,那么这个图的图扩散就定义为:
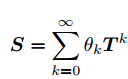 ,其中
,其中是加权系数,
是广义转移矩阵,
和
的选择必须保证上面的公式收敛,在本文中,其限制为:
![]() ,T的特征值
,T的特征值被限制在区间 [0, 1],这样就能保证矩阵收敛,常规图扩散通常要求T是列随机或行随机的。
转移矩阵(Transition matrix)
转移矩阵包括随机行走转移矩阵![]() 和对称转移矩阵
和对称转移矩阵![]() ,其中度矩阵D是节点度的对角矩阵
,其中度矩阵D是节点度的对角矩阵![]() ,在本文的定义中,
,在本文的定义中,是列随机的,并且还通过向原始邻接矩阵添加(加权)自循环来调整随机游走
![]() ,在这个公式中,
,在这个公式中,是用来调整的自循环参数。这相当于以概率P执行一种称为“懒惰随机游走”的操作,其中P是指在节点i处保持不动的概率。
![]()
图扩散的两个流行的例子是个性化页面排名(PPR)和热度核,
PPR对应于![]() ,传送概率为
,传送概率为
热度核对应于![]() ,t为扩散diffusion time
,t为扩散diffusion time
Graph diffusion convolution:
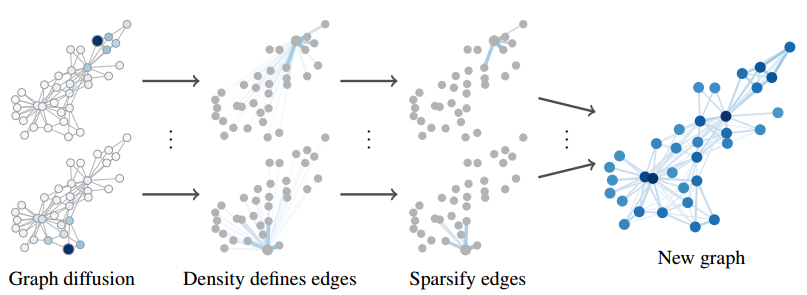
GDC的图示。通过图扩散和稀疏化将图A转换成新的图S,并在该图上运行给定的模型。本质上,图扩散卷积(GDC)就是用广义图扩散矩阵S的稀疏版本替换了正常的邻接矩阵A。该矩阵定义了一个加权有向图,本文旨在增强模型应用于该图,加权边有助于GDC的应用,但GDC也可以用于仅支持未加权边的模型,如度校正随机块模型(DCSBM),也可以通过
![]() 把图变成无向图(当想用谱聚类的时候),这样GDC基本可以适用于任何基于图的模型或算法
把图变成无向图(当想用谱聚类的时候),这样GDC基本可以适用于任何基于图的模型或算法
Intuition:
GDC背后的一般直觉是,图形扩散平滑了图形上的邻域,充当了一种类似于图像上的高斯滤波器的去噪滤波器。真实图像的特征和边往往都带有噪声,基于图扩散的平滑确实从噪声图中恢复了有意义的领域。
稀疏化(Sparsification):
大多数图形扩散会产生一个密集矩阵S,即使在这个公式 ,不把k相加,也会发生这种情况,这是因为现实生活中的“four/six degrees of separation”,即大部分节点之间存在着较短的路径,这通常导致S中的值的影响高度局部化。
,不把k相加,也会发生这种情况,这是因为现实生活中的“four/six degrees of separation”,即大部分节点之间存在着较短的路径,这通常导致S中的值的影响高度局部化。
而空间局部性允许我们截断S中的小值,从而恢复稀疏性,最终得到一个稀疏矩阵。
本文考虑两种稀疏化方案:1、top-k:使用每列质量最大的k个元素 2、阈值:设
置低于
的项为零。
虽然稀疏化需要计算密集矩阵S,但许多图扩散方法都有高效准确的近似算法,使得整个处理过程具有较低的时间和空间复杂度(通常是O(N))。此外,稀疏化还可以通过生成正则图来适用于批处理方法(甚至有助于提高预测准确度)
限制:GDC基于同质性假设,节点之间的扩散过程更多地考虑了节点之间的相似性,从而更准确地捕捉了网络中的局部结构和特征。如果想扩展到异质性,可以考虑给边负权重
GDC:
GDC总共包括四个步骤:1、计算转移矩阵T ;2、通过这个公式![]() 得到S;3、通过截断S的小值来稀疏化矩阵;4、最终得到计算转移矩阵
得到S;3、通过截断S的小值来稀疏化矩阵;4、最终得到计算转移矩阵。
第一步:过渡矩阵 T 的计算影响了使用哪种拉普拉斯矩阵来分析图的谱结构。具体来说,可以使用对称归一化拉普拉斯矩阵 或随机游走归一化拉普拉斯矩阵
,而不是未归一化的拉普拉斯矩阵
。(添加自循环会缩小图的特征值)
第二步:对求和,求和不影响原始矩阵的特征向量
![]()
![]() ,
,
对于特征向量以及对应的特征值
,特征值被公式
![]() 改变。
改变。
对于PPR,![]() ,
,
对于热核,![]()
PPR和热核都作为低通滤波器,低特征值会被放大,更好地突出和捕捉图中的大规模结构,高特征值会被抑制,从而减少对图中细节或噪声的影响。

第三步:稀疏化改变了特征值和特征向量,这意味着和
的特征值之间没有直接对应关系,但是可以使用特征值扰动理论(eigenvalue perturbation theory)来得到一个上界。
 ,其中
,其中是扰动矩阵,
是阈值。使用扰动矩阵E和阈值ϵ推导出的上界明显高估了扰动的大小。这是因为在实际情况中,基于PPR和热核的方法在真实世界的图上都表现出很强的局部化特性,因此特征值的变化经验上不会随着节点数N而扩大。典型的稀疏化阈值几乎不会对特征值产生影响。
 如图所示,基本没有影响,引起的微小变化也主要影响最高和最低的特征值。最高的特征值对应于非常大的集群和长距离的相互作用,这些对于局部图平滑来说不理想。最低的特征值则对应于虚假的振荡,这些对于图学习也没有帮助,可能是由于在阈值ϵ 处的突然截断而受到影响。
如图所示,基本没有影响,引起的微小变化也主要影响最高和最低的特征值。最高的特征值对应于非常大的集群和长距离的相互作用,这些对于局部图平滑来说不理想。最低的特征值则对应于虚假的振荡,这些对于图学习也没有帮助,可能是由于在阈值ϵ 处的突然截断而受到影响。
第四步:的转移矩阵:最后计算结果图
上的转移矩阵。此步骤不仅仅改变我们考虑的拉普拉斯算子,因为我们已经在步骤 1 中切换到使用转移矩阵。此外,它不保留特征向量,因此最好通过对特征值进行排序来进行实证研究
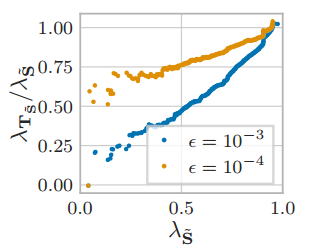 使用转移矩阵的主要目的是确保稀疏化不会因丢失不同数量的相邻边而导致节点被区别对待。滤波只是side-effect
使用转移矩阵的主要目的是确保稀疏化不会因丢失不同数量的相邻边而导致节点被区别对待。滤波只是side-effect