题目链接：最长递增路径

题目：

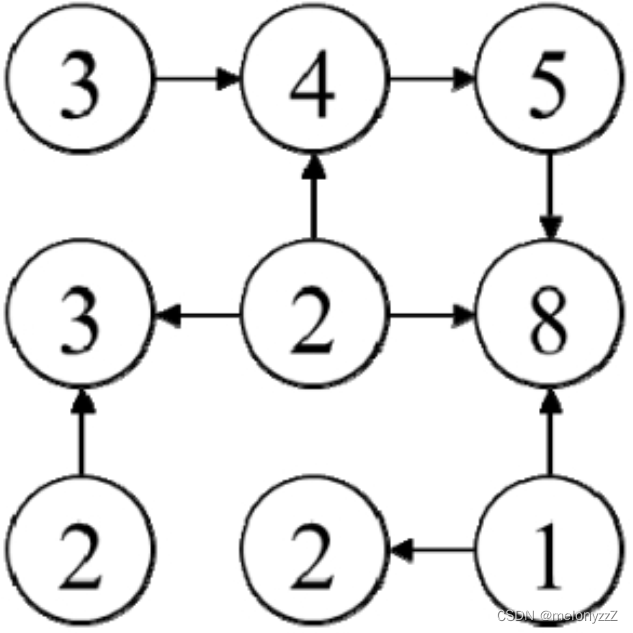
输入一个整数矩阵，请求最长递增路径的长度。矩阵中的路径沿着上、下、左、右 4 个方向前行。例如，下图中矩阵的最长递增路径的长度为 4，其中一条最长的递增路径为 3->4->5->8，如阴影部分所示。

分析：

这又是一个以矩阵为背景的经典题目。仍然可以将矩阵中的数字看成图中的节点。由于这个问题是关于递增路径的，因此只关心从较小的数字指向较大的数字的边，两个不同数字在图中对应的节点之间的边是有向边，针对这个问题构建出来的图是一个有向图。同时，由于图中所有边都是从较小的数字指向较大的数字，这样的边不可能形成环，因此构建出来的图一定是有向无环图。例如，根据上图中的矩阵构建的有向无环图如下图所示。

接着考虑如何计算图中最长递增路径的长度。由于需要搜索图中的所有节点才能确定最长递增路径的长度，因此这也是一个关于图搜索的问题。解决图搜索通常用广度优先搜索和深度优先搜索这两种不同的方法。这个问题中的路径是非常关键的信息，而深度优先搜索能够很方便地记录搜索地路径，因此深度优先搜索更适合这个问题。

因为不知道从哪个节点开始的递增路径是最长的，所以试着找出从矩阵的每个数字出发的最长递增路径的长度，通过比较可以得出整个矩阵中的最长递增路径的长度。

代码实现：

class Solution {
public:
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        int rows = matrix.size(), cols = matrix[0].size();
        vector<vector<int>> lengths(rows, vector<int>(cols, 0));
        int longest = 0;
        for (int i = 0; i < rows; ++i)
        {
            for (int j = 0; j < cols; ++j)
            {
                int length = dfs(matrix, lengths, i, j);
                longest = max(longest, length);
            }
        }
        return longest;
    }
private:
    int dfs(vector<vector<int>>& matrix, vector<vector<int>>& lengths, int i, int j) {
        if (lengths[i][j] != 0)
            return lengths[i][j];
        
        int rows = matrix.size(), cols = matrix[0].size();
        vector<vector<int>> dirs = { { -1, 0 }, { 1, 0 }, { 0, -1 }, { 0, 1 } };
        int length = 1;
        for (vector<int>& dir : dirs)
        {
            int r = i + dir[0];
            int c = j + dir[1];
            if (r >= 0 && r < rows && c >= 0 && c < cols && matrix[r][c] > matrix[i][j])
            {
                int path = dfs(matrix, lengths, r, c);
                length = max(length, path + 1);
            }
        }
        lengths[i][j] = length;
        return length;
    }
};

上述代码创建了一个与输入矩阵 matrix 大小相同的矩阵 lengths，lengths[i][j] 保存的是从矩阵中坐标为 (i, j) 的数字出发的最长递增路径的长度，然后通过比较得出矩阵中最长的递增路径的长度 longest。

矩阵 lengths 的所有值都初始化为 0，而以矩阵中某个坐标为起点的最长递增路径的长度至少是 1，所以如果 lengths[i][j] 的值大于 0，就说明之前已经计算过以坐标 (i, j) 为起点的最长递增路径的长度，如果在计算以其他坐标为起点的最长递增路径的长度时需要用到以坐标 (i, j) 为起点的最长递增路径的长度，就没有必要再次计算，只需要直接返回就可以。即矩阵 lengths 起到了缓存的作用，能够确保以任意坐标为起点的最长递增路径的长度只需要计算一次。

由于总是沿着数字递增的方向（maxtrix[r][c] > matrix[i][j] 为 true 时）在矩阵对应的图中搜索，这相当于是在一个有向无环图中搜索，因此不会出现重复访问一个节点的情况，也无须判断一个节点之前是否访问过。