目录
1、二分模板
2、习题
1.704.二分查找
2.35.搜索插入位置
3.744. 寻找比目标字母大的最小字母
4.69. x 的平方根
5.1351. 统计有序矩阵中的负数
6.74. 搜索二维矩阵
7.34. 在排序数组中查找元素的第一个和最后一个位置
8.33. 搜索旋转排序数组
9.153. 寻找旋转排序数组中的最小值
10.154. 寻找旋转排序数组中的最小值 II
3、总结
1、二分模板
二分查找可谓是入门的经典算法了,有固定的模板,但是呢每个人的模板又不太一样,为什么呢?
因为就题论题,主要是边界问题,所以我们需要在做题中,打造一个专属于自己的模板,一看就懂,即使是需要做一点小变化,自己写起来也能得心应手,
下面是我自己的二分模板:
int l = 1, r = n;
while (l < r) {
int mid = l+(r-l)/2;
if (mid > target)
l = mid + 1;//因为mid当前这个值不可能等于target了
//所以l更新为mid+1,在[mid+1,r]上查找
else
r = mid;//因为mid当前这个值可能等于target了
//所以r更新为mid,在[l,mid]上查找
}
return r;这个模板是在 [1,n] 上查找target,跳出循环时 l==r 所以我们最终返回还是r,都是一样的;
这里的 int mid = l+(r-l)/2 我用的是向下调整,但为什么是这个模式呢?
l+(r-l)/2
=l+r/2-l/2
=l/2+r/2
=(l+r)/2
写成(l+r)可能会爆int,就是超出int范围,有点危险,所以写成l+(r-l)/2,就可以避免这个问题;
了解了二分模板,我们来做几道题练习一下:
2、习题
题目来源均为LeetCode
1.704.二分查找

注意事项:
标准二分查找,套上面我给的模板,最后加个判断条件,如果当前数不是target,返回-1;
int search(int* nums, int numsSize, int target) {
int l=0,r=numsSize-1;
while(l<r)
{
int mid = l + (r - l) / 2;
if(nums[mid]<target)
l=mid+1;
else
r=mid;
}
if(nums[r]!=target)
return -1;
return r;
}2.35.搜索插入位置

注意事项;
如果数组中存在target,直接返回其下标,若不存在,我们需要二次判断,如果target大于当前值,则返回当前值的下标+1,如果target<=当前值,则返回当前值的下标;
int searchInsert(int* nums, int numsSize, int target) {
int l = 0, r = numsSize - 1;
while (l < r) {
int mid = l + (r - l) / 2;
if (nums[mid] < target)
l = mid + 1;
else
r = mid;
}
if (target > nums[r])
return r + 1;
return r;
}3.744. 寻找比目标字母大的最小字母
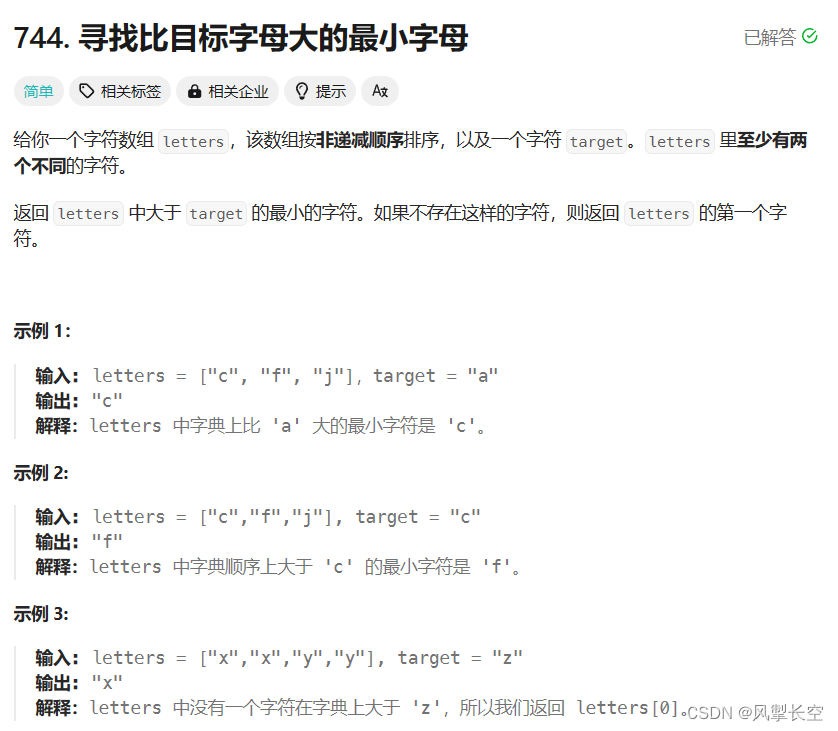
注意事项:
这个题目数组是按照非递减排序的,就是可能有重复元素,所以我们就要优化一下我们的二分模板,采用下面的二分模板,可以取到重复元素中最右边的值,然后最后再判断一下target和当前值的关系,所以我们要就题论题,,二分法往往不是一次就能做对的,多次调试次才可以;
char nextGreatestLetter(char* letters, int lettersSize, char target) {
int l = 0, r = lettersSize - 1;
// target比所有目标值都大,返回letters[0]
if (target >= letters[r])
return letters[0];
// 二分查找
while (l < r) {
int mid = l + (r - l + 1) / 2; // 向上取整
if (letters[mid] > target)
r = mid - 1;
else
l = mid;
}
// 如果target大于等于当前值,那么就返回当前值的下一个
if (target >= letters[r])
return letters[r + 1];
// 如果target小于当前值,就返回当前值
return letters[r];
}4.69. x 的平方根

注意事项:
用二分法解决数学问题,还是那个模板,本质是不变的,但是我们要考虑数学问题
int mySqrt(int x) {
//如果x==1,直接返回1
if (x == 1)
return 1;
//要开 long long类型,不然会超出范围
long long l = 1, r = x;
while (l < r) {
long long mid = l + (r - l) / 2;
if (mid * mid < x)
l = mid + 1;
else
r = mid;
}
//返回的r要么r*r刚好等于x,直接返回r就好了,要么大于x,所以要返回r-1
if (r * r == x)
return r;
return r - 1;
}5.1351. 统计有序矩阵中的负数

注意事项:
相信做到这里,你已经对二分查找有了不少理解吧,那么这道题可能对你来说不难。难的是格式的掌控,不太明白矩阵(也就是二维数组)的格式书写,当我们掌握了格式,对每一行的数据进行二分查找,就很简单了。
int binarysearch(int** grid, int i, int col) {
int l = 0, r = col-1;
while (l < r) {
int mid = (l + r) / 2;
if (grid[i][mid] >= 0)
l = mid + 1;
else
r = mid;
}
if (grid[i][r] >= 0)
return 0;//如果没有负数,返回0
return col - r;//返回负数的个数
}
int countNegatives(int** grid, int gridSize, int* gridColSize) {
// row是行 col是列
int row = gridSize, col = *gridColSize;
int sum = 0;
for (int i = 0; i < row; i++) {
sum += binarysearch(grid, i, col);
}
return sum;
}6.74. 搜索二维矩阵
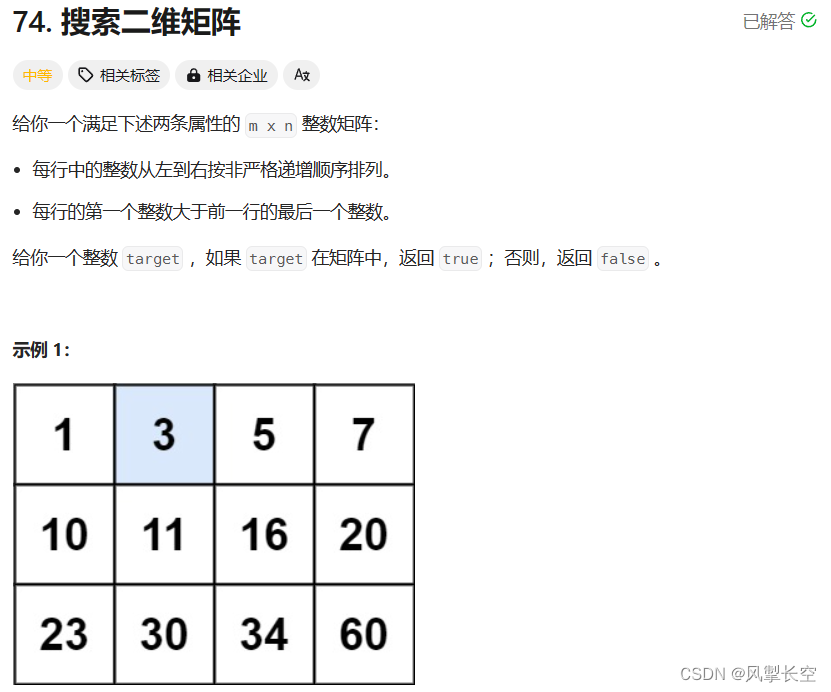
注意事项:
按照我的思路,先判断target是否存在矩阵中,如果存在,判断最后一列的每一行,确定target存在哪一行,然后在这一行中找到target,如果找不到,返回false;
bool searchMatrix(int** matrix, int matrixSize, int* matrixColSize,
int target) {
int row = matrixSize;
int col = *matrixColSize;
//判断target不属于矩阵
if (target > matrix[row - 1][col - 1] || target < matrix[0][0])
return false;
//判断target是在第r行还是第r+1行
int l = 0, r = row - 1;
while (l < r) {
int mid = l + (r - l) / 2;
if (matrix[mid][col - 1] < target)
l = mid + 1;
else
r = mid;
}
if (target > matrix[r][col - 1])
// r+1行查找
{
int l1 = 0, r1 = col - 1;
while (l1 < r1) {
int mid = l1 + (r1 - l1) / 2;
if (matrix[r + 1][mid] < target)
l1 = mid + 1;
else
r1 = mid;
}
if (matrix[r + 1][l1] == target)
return true;
}
//在第r+1行查找
else {
int l2 = 0, r2 = col - 1;
while (l2 < r2) {
int mid = l2 + (r2 - l2) / 2;
if (matrix[r][mid] < target)
l2 = mid + 1;
else
r2 = mid;
}
if (matrix[r][l2] == target)
return true;
}
return false;
}7.34. 在排序数组中查找元素的第一个和最后一个位置

注意事项:
题上要求用O(logN)的时间复杂度,我们就知道是用二分了,我的思路是先malloc一个数组,并初始化两个元素都为-1,然后查找两个目标值,用两个二分查找,不过两个二分查找的写法有点差别,但当然这两种写法,我们前面做的题都用过了,相信大家画图理解一下也是可以的;
int* searchRange(int* nums, int numsSize, int target, int* returnSize) {
// 初始化arr
int* arr = malloc(sizeof(int) * 2);
*returnSize = 2;
arr[0] = -1;
arr[1] = -1;
// 数组为空的情况
if (numsSize == 0)
return arr;
// 查找目标值的开始位置
int l = 0, r = numsSize - 1;
while (l < r) {
int mid = l + (r - l) / 2;
if (nums[mid] < target)
l = mid + 1;
else
r = mid;
}
if (nums[r] == target) {
arr[0] = r;
}
// 查找目标值的结束位置
l = 0, r = numsSize - 1;
while (l < r) {
int mid = l + (r - l + 1) / 2; // 向上取整,避免死循环
if (nums[mid] <= target)
l = mid;
else
r = mid - 1;
}
if (nums[r] == target) {
arr[1] = r;
}
// 数组中不存在目标值,直接返回arr
return arr;
}8.33. 搜索旋转排序数组

注意事项:
一开始我也没有想出来,看的题解,总结一下就是比较复杂的二分(这里的复杂是比较难想,逻辑性比较强,二分的本质是不变的),注释写的比较详细,大家可以结合示例看看,要是不理解的地方可以在评论区留言呀!
int search(int* nums, int numsSize, int target) {
int l = 0, r = numsSize - 1;
while (l <= r) {//如果数组中存在目标值,最终l==r,返回mid
int mid = l + (r - l) / 2;//取中点mid,防止 l+r 爆int
if (nums[mid] == target)
return mid;
//[l,mid]在前半部分
if (nums[l] <= nums[mid]) {
if (target >= nums[l] && target < nums[mid])
r = mid - 1;//如果target在前半部分,更新r的位置
else
l = mid + 1;//如果target在后半部分,更新l的位置
}
//[mid+1,r]在后半部分
else {
if (target > nums[mid] && target <= nums[r])
l = mid + 1; //如果target在后半部分,更新l的位置
else
r = mid - 1;//如果target在前半部分,更新r的位置
}
}
//如果数组中不存在目标值,返回-1
return -1;
}9.153. 寻找旋转排序数组中的最小值

注意事项:
看代码注释!
两种方法:
法一:找到最大值,然后最大值的后面就是最小值
int findMin(int* nums, int numsSize) {
int l = 0, r = numsSize - 1;
//假设该数组经过n次旋转还是有序的,返回数组的最小值,也就是数组的首元素
if(nums[l]<=nums[r])
return nums[l];
//注意这个地方是nums[mid]和nums[l]比较,并且mid是向上取整的
//这种方法是找到数组的最大值,然后再最大值的下标+1,得到最小值
while (l < r) {
int mid = (r+l+1) / 2;
if (nums[mid] > nums[l])
l = mid;
else
r = mid-1;
}
return nums[r+1];
}法二:直接找最小值
int findMin(int* nums, int numsSize) {
int l = 0, r = numsSize - 1;
while (l < r) {
int mid = (r + l) / 2;
if (nums[mid] > nums[r])
l = mid + 1;
else
r = mid;
}
return nums[r];
}就是两种方法的边界处置不太一样;
10.154. 寻找旋转排序数组中的最小值 II

注意事项:
这道题和上一道题比,多了重复的元素, 解法就是当nums[mid]==nums[r]时,--r,就可以巧妙的解决这个问题,你问我怎么知道的,多次实践+看题解,题解里面大佬多,就会了;
int findMin(int* nums, int numsSize) {
int l = 0, r = numsSize - 1;
while (l < r) {
int mid = l + (r - l) / 2;
if (nums[mid] > nums[r])
l = mid + 1;
else if (nums[mid] == nums[r])
--r;
else
r = mid;
}
return nums[r];
}3、总结
二分查找经典并不简单,要从实践中总结经验,还是要多练,菜就多练
多多重复,百炼成钢!