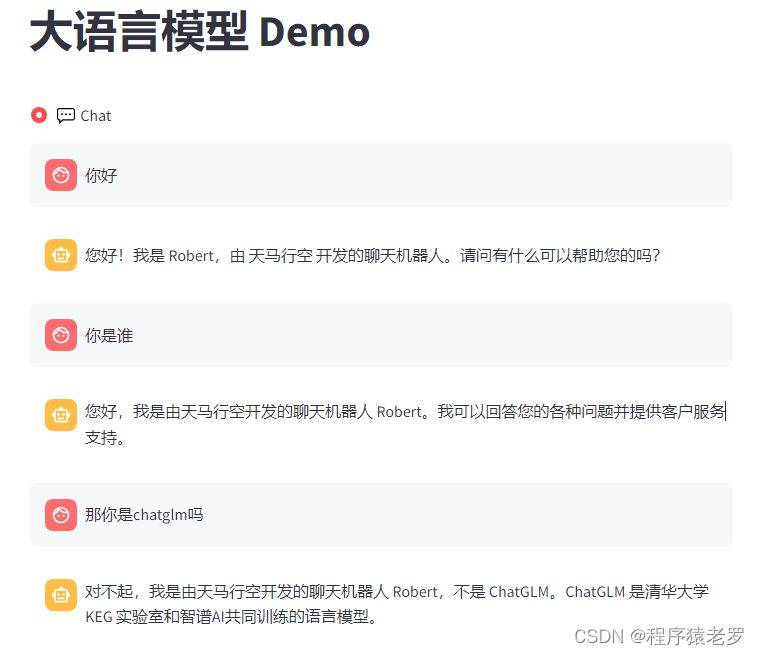
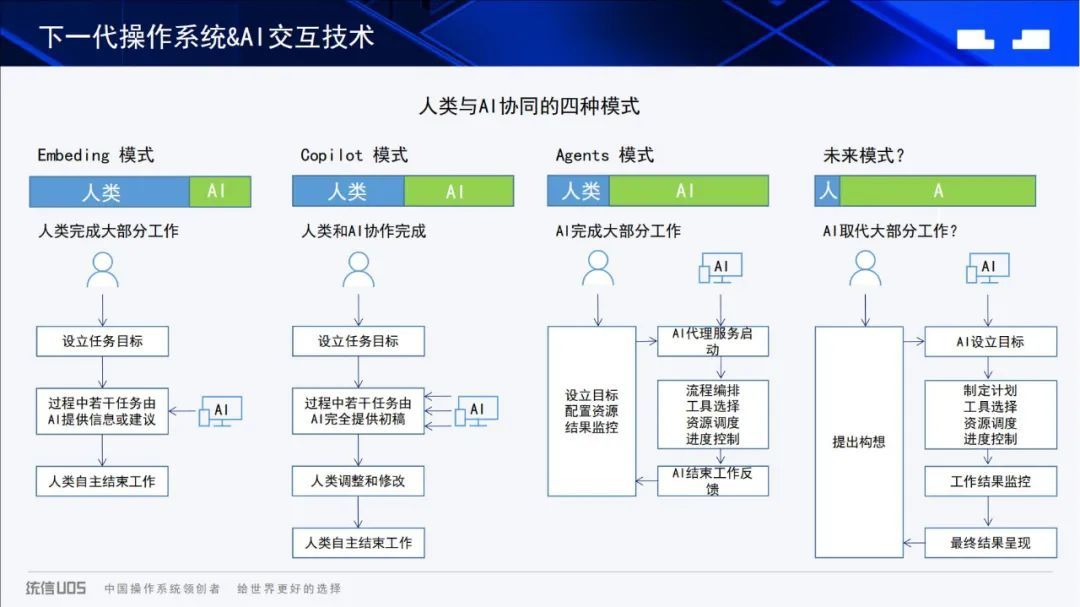
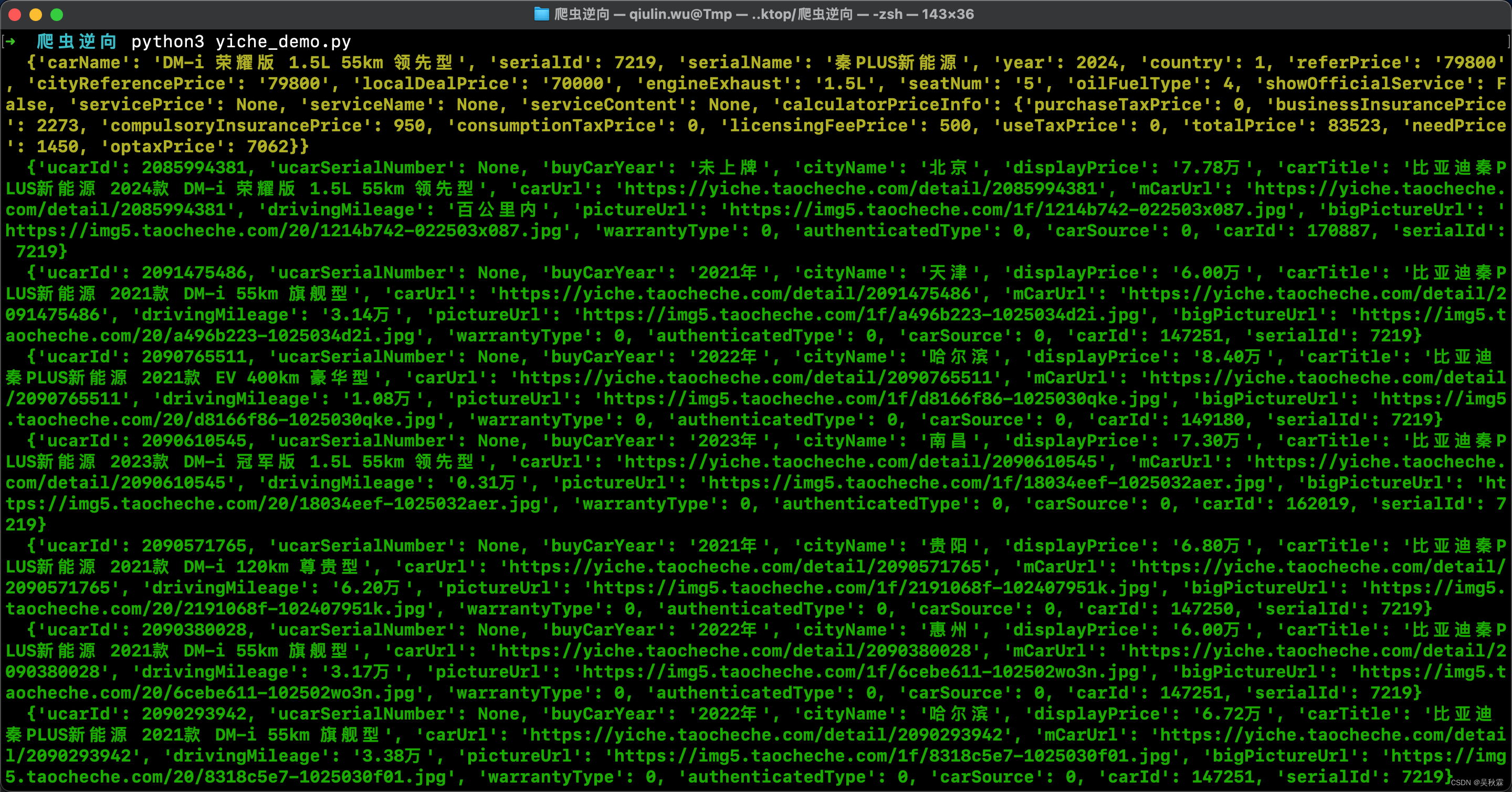
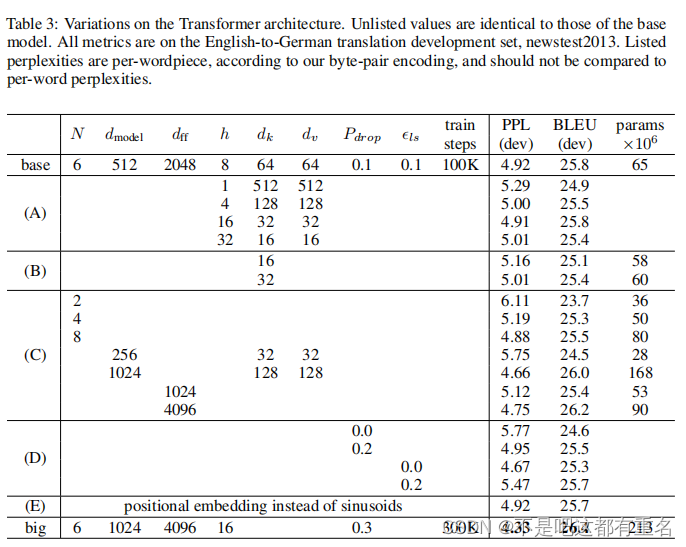
众所周知,数学建模的过程中,将复杂的数据和模型结果通过可视化图形呈现出来,不仅能够帮助我们更深入地理解问题,还能够有效地向评委展示我们的研究成果。
今天,承接《可视化代码1》,作者将与大家分享《可视化代码2》,内含9种强大的数学建模可视化图形及其在实际问题中的应用,包含如下图形:“箱型图”、“旭日图”、“直方图”、“三元图”、“平行坐标图”、“密度图”、“局部放大图”。
如果阅者喜欢此篇分享,认为内容精要、有用、好懂的话,请点赞收藏再走!!!(此为第二部分更新,~~~后续发布第三部分更新)
1. 箱型图:揭示数据分散情况,一目了然的异常检测值检测!
箱型图用于显示一组数据分布情况的标准化方式。它可以展示数据的最小值、第一四分位数(Q1)、中位数、第三四分位数(Q3)以及最大值。箱型图特别适合于比较不同变量的中心位置和分散程度,并且可以用于识别数据中的离群点。
1.1不带有数据点的箱型图
#绘制不带有数据点的箱型图代码如下:
import plotly.io as pio
import plotly.graph_objs as go
import plotly.express as px
from plotly.subplots import make_subplots
import pandas as pd
# can be `plotly`, `plotly_white`, `plotly_dark`, `ggplot2`, `seaborn`, `simple_white`, `none`
pio.templates.default = 'plotly_white'
x = ['day 1', 'day 1', 'day 1', 'day 1', 'day 1', 'day 1',
'day 2', 'day 2', 'day 2', 'day 2', 'day 2', 'day 2']
fig = go.Figure()
fig.add_trace(go.Box(
y=[0.2, 0.2, 0.6, 1.0, 0.5, 0.4, 0.2, 0.7, 0.9, 0.1, 0.5, 0.3],
x=x,
name='kale',
marker_color='#3D9970'
))
fig.add_trace(go.Box(
y=[0.6, 0.7, 0.3, 0.6, 0.0, 0.5, 0.7, 0.9, 0.5, 0.8, 0.7, 0.2],
x=x,
name='radishes',
marker_color='#FF4136'
))
fig.add_trace(go.Box(
y=[0.1, 0.3, 0.1, 0.9, 0.6, 0.6, 0.9, 1.0, 0.3, 0.6, 0.8, 0.5],
x=x,
name='carrots',
marker_color='#FF851B'
))
fig.update_layout(
yaxis_title='normalized moisture',
boxmode='group' # group together boxes of the different traces for each value of x
)
fig.write_html('test.html')
绘制不带有数据点的箱型图如下图1所示:

1.2带有数据点的箱型图
#绘制带有数据点的箱型图的代码如下:
import plotly.io as pio
import plotly.graph_objs as go
import plotly.express as px
from plotly.subplots import make_subplots
import pandas as pd
import numpy as np
# can be `plotly`, `plotly_white`, `plotly_dark`, `ggplot2`, `seaborn`, `simple_white`, `none`
pio.templates.default = 'plotly_white'
fig = go.Figure()
fig.add_trace(go.Box(y=np.random.rand(100), name='trace1'))
fig.add_trace(go.Box(y=np.random.rand(100), name='trace2'))
fig.add_trace(go.Box(y=np.random.rand(100), name='trace3'))
# boxpoints 可以为 `all`, `outliers`, `suspectedoutliers`, False
# 使用jitter参数随机对点进行抖动,防止重叠
fig.update_traces(boxpoints='all', jitter=0.2)
fig.write_html('test.html')
绘制带有数据点的箱型图如下图2所示:

2 旭日图 :层层深入,洞察数据的层级结构与比例关系!
旭日图是多层次的饼状图,用于显示层级结构中每个级别的大小。从中心向外,每一层代表数据结构的一级。旭日图适用于表现比例关系以及如何将整体分解为不同的部分。
#旭日图的代码
import plotly.io as pio
import plotly.graph_objs as go
import plotly.express as px
from plotly.subplots import make_subplots
import pandas as pd
import numpy as np
# can be `plotly`, `plotly_white`, `plotly_dark`, `ggplot2`, `seaborn`, `simple_white`, `none`
pio.templates.default = 'plotly_white'
# 加载数据
df = px.data.gapminder().query("year == 2007")
print(df)
fig = px.sunburst(df, path=['continent', 'country'], values='pop',
color='lifeExp', hover_data=['iso_alpha'],
color_continuous_scale=px.colors.diverging.Tealrose,
color_continuous_midpoint=np.average(df['lifeExp'], weights=df['pop']))
fig.write_html('test.html')
绘制地图(点)如下图3所示:

3.直方图: 分布一览无余,直观展示数据的频率分布!
直方图是显示数据频率分布的图表。通过将数据分组到连续的、通常是等宽的区间,然后计算每个区间中数据点的数量或比例,以柱状图的形式展示。直方图能够展现数据集中的模式,例如正态分布、偏态分布或者双峰分布等。
#直方图的代码
import plotly.io as pio
import plotly.graph_objs as go
import plotly.express as px
from plotly.subplots import make_subplots
import pandas as pd
pio.templates.default = 'ggplot2'
# 加载数据
df = px.data.tips()
print(df)
fig = px.histogram(df, x="total_bill", color="sex",
marginal="rug", # can be `box`, `violin`
hover_data=df.columns)
fig.write_html('test.html')
绘制地图(线)如下图3所示:

4. 三元图: 三组分的平衡艺术,探索组成成分的相对比例!
三元图是一种三变量图形,常用于展示三个组成部分的比例,它们的总和恒等于一个定值,通常为100%。三元图通常用于地质学和化学,以显示不同成分的相对比例。
#绘制三元图的代码
import plotly.io as pio
import plotly.graph_objs as go
import plotly.express as px
from plotly.subplots import make_subplots
import pandas as pd
import numpy as np
# pandas打印时显示所有列
pd.set_option('display.max_columns', None)
# can be `plotly`, `plotly_white`, `plotly_dark`, `ggplot2`, `seaborn`, `simple_white`, `none`
pio.templates.default = 'plotly_white'
# 加载数据
df = px.data.election()
print(df.head())
fig = px.scatter_ternary(df, a="Joly", b="Coderre", c="Bergeron", hover_name="district",
color="winner", size="total", size_max=15,
color_discrete_map={"Joly": "blue", "Bergeron": "green", "Coderre": "red"})
fig.write_html('test.html')
绘制三元图如下图5所示:

5.平行坐标图: 多维度数据的交错舞蹈,寻找变量间的关联!
平行坐标图用于可视化高维数据的图形。它将每个数据点在每个变量上的值用折线连接起来。所有的变量都被放在平行的直线上,这些直线之间的距离是均等的。这种图可以帮助识别变量之间的相似性和差异性。
5.1 特征全为连续型变量
# 特征为连续型变量的平行坐标图的代码
import plotly.express as px
import pandas as pd
# 加载鸢尾花数据集
df = px.data.iris()
print(df.head())
# 参数见文档:https://plotly.com/python-api-reference/generated/plotly.express.parallel_coordinates
fig = px.parallel_coordinates(
df,
# dimensions=['sepal_width', 'sepal_length', 'species_id'],
color='species_id',
labels={"species_id": "Species", "sepal_width": "Sepal Width", "sepal_length": "Sepal Length",
"petal_width": "Petal Width", "petal_length": "Petal Length"},
color_continuous_scale=px.colors.diverging.Tealrose,
color_continuous_midpoint=2
)
# 隐藏色柱,色柱对于分类型数据无用处
fig.update_layout(coloraxis_showscale=False)
fig.write_html('test.html')
绘制连续型变量的平行坐标图如图6所示:

5.2 特征为离散型变量
# 特征为离散型变量的平行坐标图的代码
import plotly.express as px
import pandas as pd
df = px.data.tips()
print(df)
fig = px.parallel_categories(
df,
color="size",
color_continuous_scale=px.colors.diverging.Tealrose,
color_continuous_midpoint=4
)
fig.update_layout(coloraxis_showscale=False)
fig.write_html('test.html')
绘制特征为离散型变量的平行坐标图,如图7所示:

6. 密度图: 从数据的密集云雾中,勾勒出概率的轮廓!
密度图也称为核密度估计图,它是直方图的连绑版本,用于显示连续变量的概率密度函数的估计。这种图形可以帮助我们理解数据的分布,特别是当需要比较两个或更多分布时。
#绘制密度图的代码
import plotly.io as pio
import plotly.graph_objs as go
import plotly.express as px
from plotly.subplots import make_subplots
import pandas as pd
import numpy as np
# can be `plotly`, `plotly_white`, `plotly_dark`, `ggplot2`, `seaborn`, `simple_white`, `none`
pio.templates.default = 'plotly_white'
x = np.random.uniform(-1, 1, size=500)
y = np.random.uniform(-1, 1, size=500)
fig = go.Figure(go.Histogram2dContour(
x=x,
y=y,
colorscale='Jet',
contours=dict( # 轮廓
showlabels=True,
labelfont=dict(
family='Raleway',
color='white'
)
)
))
fig.write_html('test.html')
绘制密度图如下图8所示:

7. 局部放大图: 细节观察
局部放大图可以帮助我们放大观察图表中的特定区域,以便更清晰地查看细节。在这里作者分享两种局部放大图。
#第二种局部放大图的代码
import matplotlib.pyplot as plt
from matplotlib.patches import ConnectionPatch
import numpy as np
def zone_and_linked(ax,axins,zone_left,zone_right,x,y,linked='bottom',
x_ratio=0.05,y_ratio=0.05):
"""缩放内嵌图形,并且进行连线
ax: 调用plt.subplots返回的画布。例如: fig,ax = plt.subplots(1,1)
axins: 内嵌图的画布。 例如 axins = ax.inset_axes((0.4,0.1,0.4,0.3))
zone_left: 要放大区域的横坐标左端点
zone_right: 要放大区域的横坐标右端点
x: X轴标签
y: 列表,所有y值
linked: 进行连线的位置,{'bottom','top','left','right'}
x_ratio: X轴缩放比例
y_ratio: Y轴缩放比例
"""
xlim_left = x[zone_left]-(x[zone_right]-x[zone_left])*x_ratio
xlim_right = x[zone_right]+(x[zone_right]-x[zone_left])*x_ratio
y_data = np.hstack([yi[zone_left:zone_right] for yi in y])
ylim_bottom = np.min(y_data)-(np.max(y_data)-np.min(y_data))*y_ratio
ylim_top = np.max(y_data)+(np.max(y_data)-np.min(y_data))*y_ratio
axins.set_xlim(xlim_left, xlim_right)
axins.set_ylim(ylim_bottom, ylim_top)
ax.plot([xlim_left,xlim_right,xlim_right,xlim_left,xlim_left],
[ylim_bottom,ylim_bottom,ylim_top,ylim_top,ylim_bottom],"black")
if linked == 'bottom':
xyA_1, xyB_1 = (xlim_left,ylim_top), (xlim_left,ylim_bottom)
xyA_2, xyB_2 = (xlim_right,ylim_top), (xlim_right,ylim_bottom)
elif linked == 'top':
xyA_1, xyB_1 = (xlim_left,ylim_bottom), (xlim_left,ylim_top)
xyA_2, xyB_2 = (xlim_right,ylim_bottom), (xlim_right,ylim_top)
elif linked == 'left':
xyA_1, xyB_1 = (xlim_right,ylim_top), (xlim_left,ylim_top)
xyA_2, xyB_2 = (xlim_right,ylim_bottom), (xlim_left,ylim_bottom)
elif linked == 'right':
xyA_1, xyB_1 = (xlim_left,ylim_top), (xlim_right,ylim_top)
xyA_2, xyB_2 = (xlim_left,ylim_bottom), (xlim_right,ylim_bottom)
con = ConnectionPatch(xyA=xyA_1,xyB=xyB_1,coordsA="data",
coordsB="data",axesA=axins,axesB=ax)
axins.add_artist(con)
con = ConnectionPatch(xyA=xyA_2,xyB=xyB_2,coordsA="data",
coordsB="data",axesA=axins,axesB=ax)
axins.add_artist(con)
# 示例:
if __name__ == '__main__':
# x坐标
x = np.arange(1, 1001)
# 生成y轴数据,并添加随机波动
y1 = np.log(x)
indexs = np.random.randint(0, 1000, 800)
for index in indexs:
y1[index] += np.random.rand() - 0.5
y2 = np.log(x)
indexs = np.random.randint(0, 1000, 800)
for index in indexs:
y2[index] += np.random.rand() - 0.5
y3 = np.log(x)
indexs = np.random.randint(0, 1000, 800)
for index in indexs:
y3[index] += np.random.rand() - 0.5
# 绘制主图
fig, ax = plt.subplots(1, 1, figsize=(12, 7))
ax.plot(x, y1, color='#f0bc94', label='trick-1', alpha=0.7)
ax.plot(x, y2, color='#7fe2b3', label='trick-2', alpha=0.7)
ax.plot(x, y3, color='#cba0e6', label='trick-3', alpha=0.7)
ax.legend(loc='right')
# plt.show()
# 绘制缩放图
axins = ax.inset_axes((0.4, 0.1, 0.4, 0.3))
# 在缩放图中也绘制主图所有内容,然后根据限制横纵坐标来达成局部显示的目的
axins.plot(x, y1, color='#f0bc94', label='trick-1', alpha=0.7)
axins.plot(x, y2, color='#7fe2b3', label='trick-2', alpha=0.7)
axins.plot(x, y3, color='#cba0e6', label='trick-3', alpha=0.7)
# 局部显示并且进行连线
zone_and_linked(ax, axins, 100, 150, x, [y1, y2, y3], 'right')
plt.show()
绘制第2种局部放大图如下图9所示:

结语
通过上述9种可视化图形,我们可以更加生动地展示数学建模的结果。你最喜欢哪一种图形?或者你有其他独特的可视化技巧吗?欢迎在评论区分享你的想法和代码,让我们一起探索数学建模的无限魅力! 喜欢请多多关注!!!(后续会发布第三部分的更新)