C语言数据结构之顺序表

news2024/11/20 14:37:19

目录

    • 1.线性表
    • 2.顺序表
      • 2.1顺序表相关概念及结构
      • 2.2增删查改等接口的实现
    • 3.数组相关例题

在这里插入图片描述

在这里插入图片描述

1.线性表

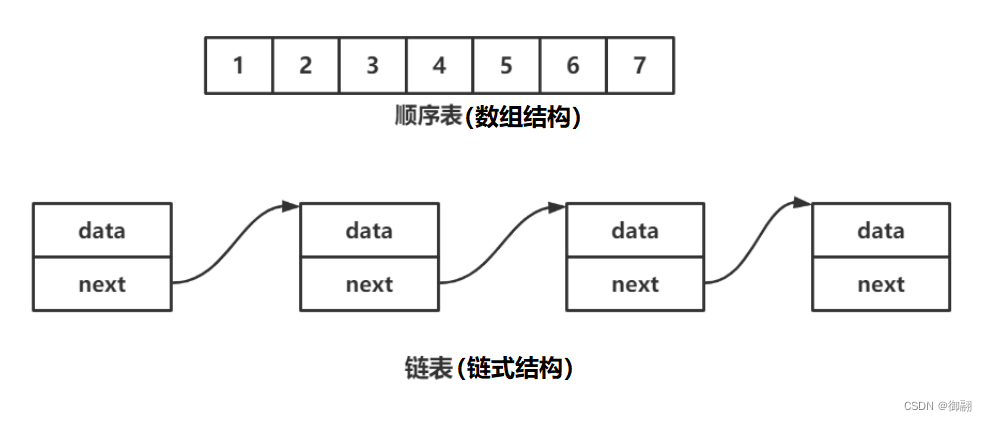
线性表（linear list）是n个具有相同特性（数据类型相同）的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构，常见的线性表：顺序表、链表、栈、队列、字符串…
线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的（ 在内存中的储存地址可能不是连续的，但是我们可以按它的储存顺序从顺序表的开头依次找到结尾，所以逻辑上是连续的 ） ，线性表在物理上存储时，通常以数组和链式结构的形式存储。
在这里插入图片描述

2.顺序表

2.1顺序表相关概念及结构

顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构，一般情况下采用数组存储。结构与数组相同，在数组的基础上增加了对数据的增删查改。

顺序表一般可以分为：
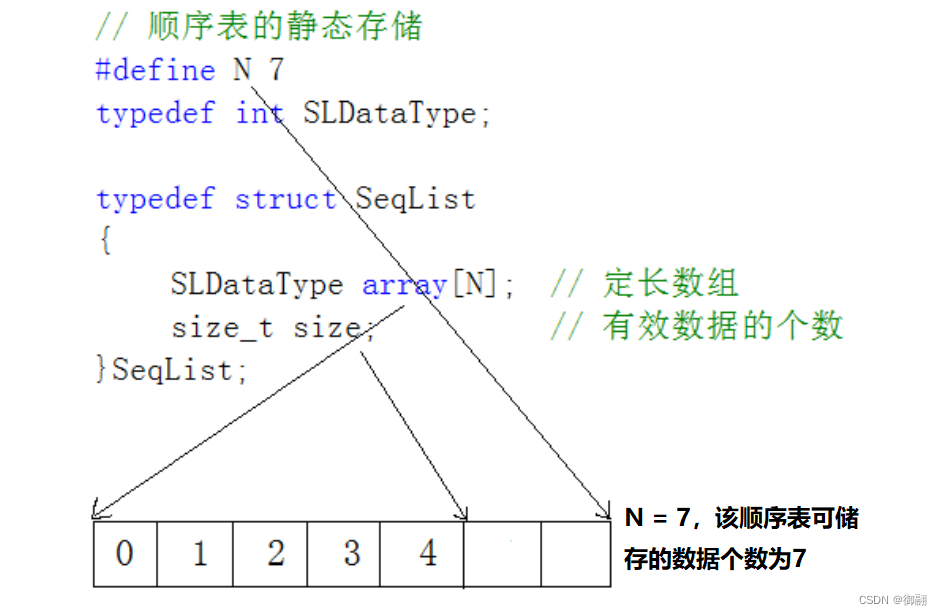
1.静态顺序表：数组的长度是确定的，不可改变。

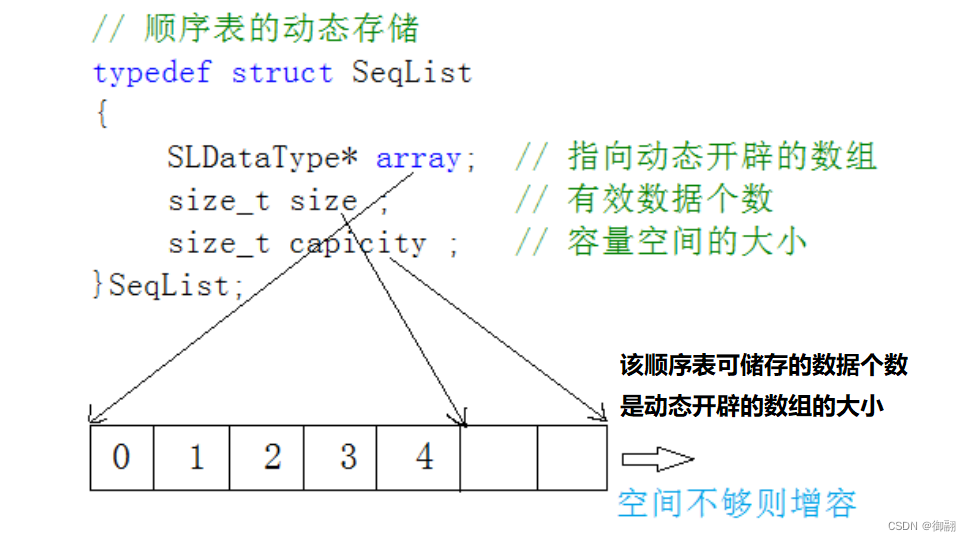
在这里插入图片描述

2.动态顺序表：使用动态开辟的数组存储数据，数组大小是可变的。

在这里插入图片描述

2.2增删查改等接口的实现

静态顺序表只适用于确定知道需要存多少数据的场景。静态顺序表的数组大小N是确定的，不能改变，N如果定大了，空间开多了浪费，N定小了，空间开少了不够用。所以现实中基本都是使用动态顺序表，根据需要改变动态分配的空间大小，可以更加灵活地储存数据，所以下面我们实现动态顺序表。

test.c

#include "SeqList.h"

void menu()//功能菜单
{
	printf("******************************************\n");
	printf("**************    请选择    **************\n");
	printf("******  1.PushFront    2.PushBack  *******\n");
	printf("******  3.PopFront     4.PopBack   *******\n");
	printf("******  5.Insert       6.Del       *******\n");
	printf("******  7.Modify       8.FindSct   *******\n");
	printf("******  9.Print        0.Exit      *******\n");
	printf("******************************************\n");
}

int main()
{
	int input = 0;
	int value = 0;
	int pos = 0;
	SeqList sl;
	Init_SeqList(&sl);
	do
	{
		menu();
		scanf("%d", &input);
		switch (input)
		{
		case 1:
			printf("请输入要头插的值>:");
			scanf("%d", &value);
			Push_Front_SeqList(&sl, value);
			break;
		case 2:
			printf("请输入要尾插的值>:");
			scanf("%d", &value);
			Push_Back_SeqList(&sl, value);
			break;
		case 3:
			Pop_Front_SeqList(&sl);
			break;
		case 4:
			Pop_Back_SeqList(&sl);
			break;
		case 5:
			printf("请输入你要插入的位置和要插入的值>:");
			scanf("%d %d", &pos, &value);
			Insert_SeqList(&sl, pos, value);
			break;
		case 6:
			printf("请输入要删除的值>:");
			scanf("%d", &value);
			Del_SeqList(&sl, value);
			break;
		case 7:
			printf("请输入你要修改的位置和修改的值:>");
			scanf("%d %d", &pos, &value);
			Modify_SeqList(&sl, pos, value);
			break;
		case 8:
			printf("请输入你要查找的值>:");
			scanf("%d", &value);
			int ret = Find_Sct_SeqList(&sl, value);
			if (ret == -1)
				printf("找不到该值\n");
			else
				printf("该值的下标为%d\n", ret);
			break;
		case 9:
			Print_SeqList(&sl);
			break;
		case 0:
			printf("退出成功\n");
			Destroy_SeqList(&sl);
		}
	} while (input);
	return 0;
}

SeqList.c

#include "SeqList.h"


//初始化顺序表
void Init_SeqList(SeqList* ptr)
{
	assert(ptr);//防止ptr为空指针，空指针不能解引用

	SLDataType* tmp = (SLDataType*)malloc(3 * sizeof(SLDataType));//先开3个数据的大小，不够再增
	
	if (tmp == NULL)//有可能动态数组开辟不成功
	{
		perror("Init_SeqList");
		exit(1);
	}
	else
		ptr->arr = tmp;

	ptr->size = 0;
	ptr->capacity = 3;
}


//销毁顺序表
void Destroy_SeqList(SeqList* ptr)//动态申请的空间使用完之后要释放，不然会造成内存泄漏
{
	free(ptr->arr);
	ptr->arr = NULL;
}


//检查数组大小
void Check_Capacity(SeqList* ptr)//数组大小不够则增容
{
	assert(ptr);//防止ptr为空指针，空指针不能解引用

	if (ptr->size == ptr->capacity)
	{
		SLDataType* tmp = (SLDataType*)realloc(ptr->arr, 2 * ptr->capacity * sizeof(SLDataType));//每次增容都开辟两倍的数组大小
		
		if (tmp == NULL)//有可能动态数组开辟不成功
		{
			perror("Check_Capacity");
			exit(1);
		}
		else
			ptr->arr = tmp;

		ptr->capacity *= 2;//扩容后不要忘记把capacity修改
	}
}


//寻找某个数据的下标
int Find_Sct_SeqList(SeqList* ptr, SLDataType val)
{
	assert(ptr);//防止ptr为空指针，空指针不能解引用

	for (int i = 0; i < ptr->size; i++)
	{
		if (ptr->arr[i] == val)
		{
			return i;//找到val返回val的下标
		}
	}
	return -1;//找不到则返回-1，因为-1不是下标，方便区分找没找到
}


//在数据dst的前面插入数据src
void Insert_SeqList(SeqList* ptr, SLDataType dst,SLDataType src)
{
	assert(ptr);//防止ptr为空指针，空指针不能解引用

	Check_Capacity(ptr);//插入前要先检查空间够不够，不够则增容

	int sct = Find_Sct_SeqList(ptr, dst);
	if(sct == -1)//有可能要插入的值的位置是不存在的
	{
		printf("找不到该值\n");
		return;
	}

	for (int i = ptr->size - 1; i >= sct ; i--)//插入一个值，后面的值都要往后移动
	{
		ptr->arr[i+1] = ptr->arr[i];
	}

	ptr->arr[sct] = src;
	ptr->size++;//插入后不要忘了给数组大小加1
}


//头插一个数据
void Push_Front_SeqList(SeqList* ptr,SLDataType val)
{
	assert(ptr);//防止ptr为空指针，空指针不能解引用

	Check_Capacity(ptr);插入前要先检查空间够不够，不够则增容

	for (int i = ptr->size - 1; i >= 0; i--)
	{
		ptr->arr[i + 1] = ptr->arr[i];
	}

	ptr->arr[0] = val;
	ptr->size++;//插入后不要忘了给数组大小加1
}


//尾插一个数据
void Push_Back_SeqList(SeqList* ptr,SLDataType val)
{
	assert(ptr);//防止ptr为空指针，空指针不能解引用

	Check_Capacity(ptr);//插入前要先检查空间够不够，不够则增容

	ptr->arr[ptr->size] = val;
	ptr->size++;//插入后不要忘了给数组大小加1
}


//修改一个给定的数据
void Modify_SeqList(SeqList* ptr, SLDataType dst, SLDataType src)
{
	assert(ptr);//防止ptr为空指针，空指针不能解引用

	int sct = Find_Sct_SeqList(ptr, dst);
	
	if (sct == -1)//有可能要修改的值是不存在的
	{
		printf("找不到该值\n");
		return;
	}
	ptr->arr[sct] = src;
}


//删除一个给定的数据
void Del_SeqList(SeqList* ptr, SLDataType val)
{
	assert(ptr);//防止ptr为空指针，空指针不能解引用

	int sct = Find_Sct_SeqList(ptr, val);
	
	if (sct == -1)//有可能要删除的值是不存在的
	{
		printf("找不到该值\n");
		return;
	}
	for (int i = sct + 1; i < ptr->size; i++)
	{
		ptr->arr[i - 1] = ptr->arr[i];
	}
	ptr->size--;
}


//头删一个数据
void Pop_Front_SeqList(SeqList* ptr)
{
	assert(ptr);//防止ptr为空指针，空指针不能解引用

	if (ptr->size == 0)//数组内元素个数为0时不能再删了，否则会越界访问
	{
		return;
	}

	for (int i = 1; i < ptr->size; i++)
	{
		ptr->arr[i - 1] = ptr->arr[i];
	}
	ptr->size--;
}


//尾删一个数据
void Pop_Back_SeqList(SeqList* ptr)
{
	if (ptr->size == 0)//数组内元素个数为0时不能再删了，否则会越界访问
	{
		return;
	}

	assert(ptr);
	ptr->size--;//数组尾删就是不访问最后一个元素，将数组大小减1就可以了
}


//打印顺序表
void Print_SeqList(SeqList* ptr)
{
	assert(ptr);//防止ptr为空指针，空指针不能解引用

	for (int i = 0; i < ptr->size; i++)
	{
		printf("%d ",ptr->arr[i]);
	}
	printf("\n");
}

SeqList.h

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <errno.h>

typedef int SLDataType; //将数据类型重命名为SLDataType，方便修改储存的数据类型

typedef struct SeqList
{
	SLDataType* arr; //动态开辟的数组
	size_t size;     //数组元素个数
	size_t capacity; //数组大小
}SeqList;

void Init_SeqList(SeqList* ptr);

void Insert_SeqList(SeqList* ptr, SLDataType dst, SLDataType src);

void Push_Front_SeqList(SeqList* ptr, SLDataType val);

void Push_Back_SeqList(SeqList* ptr, SLDataType val);

void Modify_SeqList(SeqList* ptr, SLDataType dst, SLDataType src);

void Del_SeqList(SeqList* ptr, SLDataType val);

void Pop_Front_SeqList(SeqList* ptr);

void Pop_Back_SeqList(SeqList* ptr);

int Find_Sct_SeqList(SeqList* ptr, SLDataType val);

void Print_SeqList(SeqList* ptr);

void Destroy_SeqList(SeqList* ptr);

3.数组相关例题

题目1：

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

示例 ：

输入：nums = [3, 2, 2, 3], val = 3
输出：2, nums = [2, 2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。
例如，函数返回的新长度为 2 ，而 nums = [2, 2, 3, 3] 或 nums = [2, 2, 0, 0]，也会被视作正确答案。

参考解析：

void Swap(int* a, int* b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

// 思路：用两个存下标的front和behind都先放在0的位置，front找不是val的值与behind交换，
// 这样就相当于把等于val的值往后放，不等于val的值往前放
// 最后数组的前n个数就是我们想要的删除所有val值之后的数组

int removeElement(int* nums, int numsSize, int val) 
{
    int front, behind;
    front = behind = 0;
    while (front < numsSize)
    {
        if (nums[front] == val)
        {
            front++;
        }
        else
        {
            if (front != behind)
                Swap(&nums[front], &nums[behind]);
            front++;
            behind++;
        }
    }
    return behind;//每找到一个不是val的值behind就++一次，所以behind的值就是新数组的长度
}

程序执行过程图：

在这里插入图片描述

题目2：

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。
为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1, 2, 3, 0, 0, 0], m = 3, nums2 = [2, 5, 6], n = 3
输出：[1, 2, 2, 3, 5, 6]
解释：需要合并[1, 2, 3] 和[2, 5, 6] 。
合并结果是[1, 2, 2, 3, 5, 6] ，其中斜体加粗标注的为 nums1 中的元素。

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并[1] 和[] 。
合并结果是[1] 。

参考解析：

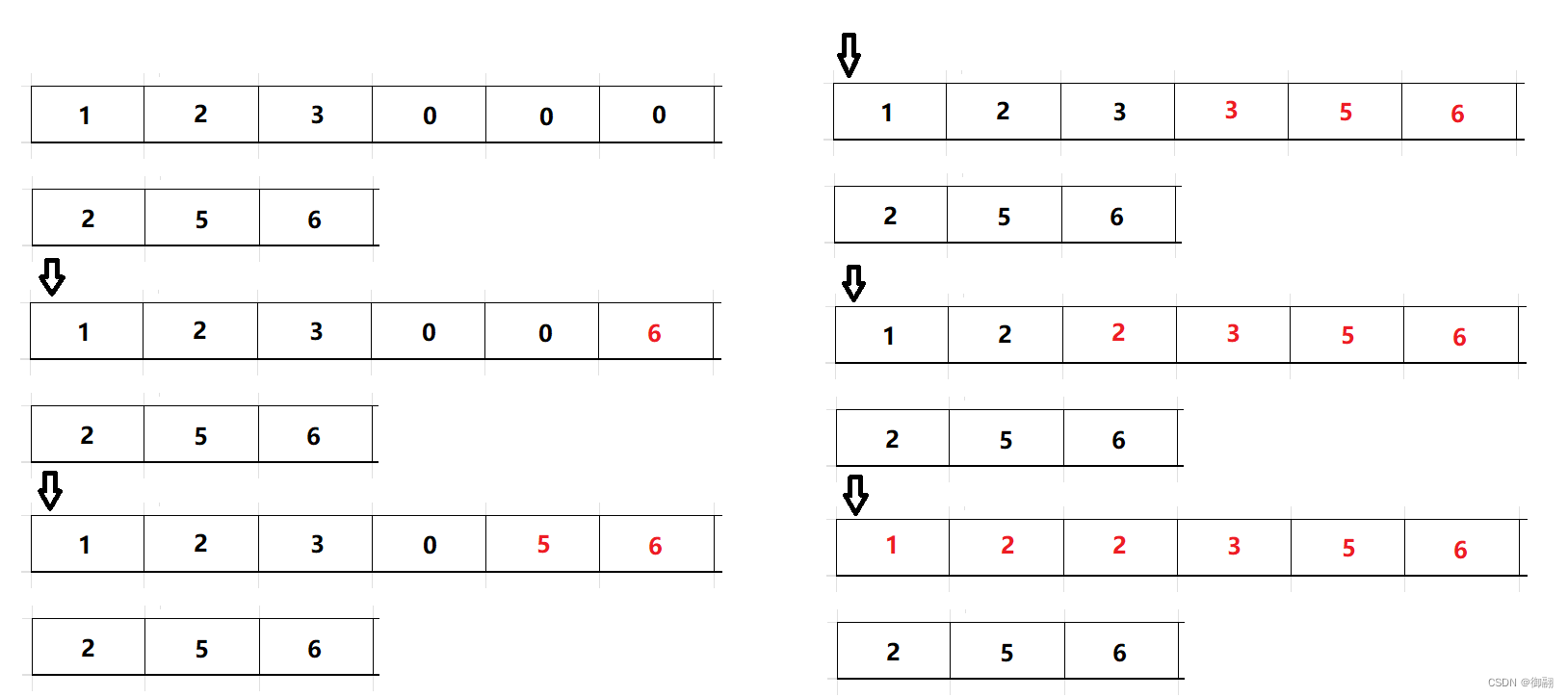
//解题思路:
//1. 从后往前遍历数组，将nums1和nums2中的元素逐个比较
//将较大的元素往nums1末尾进行搬移
//2. 第一步结束后，nums2中可能会有数据没有搬移完，将nums2中剩余的元素逐个搬移到nums1
//
//时间复杂度：O(m + n)
//空间复杂度 : O(1)

void Merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)
{
    // end1、end2：分别标记nums1 和 nums2最后一个有效元素位置
	// end标记nums1的末尾，nums1和nums2中的元素从后往前往nums1中存放，应从end开始往前放，否则会存在数据覆盖
    int end1 = m - 1;
    int end2 = n - 1;
    int index = m + n - 1;


    // 从后往前遍历，将num1或者nums2中较大的元素往num1中end位置搬移
    // 直到将num1或者num2中有效元素全部搬移完
    while (end1 >= 0 && end2 >= 0)
    {
        if (nums1[end1] > nums2[end2])
        {
            nums1[index--] = nums1[end1--];
        }
        else
        {
            nums1[index--] = nums2[end2--];
        }
    }


    // num2中的元素可能没有搬移完，将剩余的元素继续往nums1中搬移
    while (end2 >= 0)
    {
        nums1[index--] = nums2[end2--];
    }


    // num1中剩余元素没有搬移完 ---不用管了，因为num1中剩余的元素本来就在num1中
}

程序执行过程图：

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1609750.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【RV1106的ISP使用记录之基础知识】硬件连接关系与设备树的构建

【RV1106的ISP使用记录之基础知识】硬件连接关系与设备树的构建

RV1106具备2个mipi csi2 dphy硬件&#xff0c;1个VICAP硬件和1个ISP硬件。其中&#xff1a; 1、mipi csi2 dphy 用于对数据流的解析&#xff0c;支持MIPC,LVDS,DVP三种接口&#xff1b; 2、VICAP用于数据流的捕获&#xff1b; 3、ISP用于对图像数据进行处理&#xff1b; 这三个…
阅读更多...
【QTM中文教程】01：Quick Terrain Modeller介绍、下载与安装

【QTM中文教程】01：Quick Terrain Modeller介绍、下载与安装

文章目录 一、Quick Terrain Modeller简介二、Quick Terrain Modeller特点功能三、Quick Terrain Modeller下载安装1. 下载地址2. 安装教程一、Quick Terrain Modeller简介 Quick Terrain Modeler（QTM）是一种专业的地形建模软件，用于处理和分析地形数据。它提供了一系列功能…
阅读更多...
【漏洞复现】泛微e-cology ProcessOverRequestByXml接口存在任意文件读取漏洞

【漏洞复现】泛微e-cology ProcessOverRequestByXml接口存在任意文件读取漏洞

漏洞描述 泛微e-cology依托全新的设计理念,全新的管理思想。 为中大型组织创建全新的高效协同办公环境。 智能语音办公,简化软件操作界面。 身份认证、电子签名、电子签章、数据存证让合同全程数字化。泛微e-cology ProcessOverRequestByXml接口存在任意文件读取漏洞 免责声…
阅读更多...
【漏洞复现】宏景eHR showmediainfo SQL注入漏洞

【漏洞复现】宏景eHR showmediainfo SQL注入漏洞

0x01 产品简介 北京宏景世纪软件股份有限公司&#xff08;简称“宏景软件”&#xff09;专注于国有企事业单位人力与人才管理数智化&#xff08;数字化、智能化&#xff09;产品的研发和应用推广。 0x02 漏洞概述 宏景eHR /workbench/duty/showmediainfo接口存在SQL注入漏洞…
阅读更多...
Jenkins用maven风格build报错解决过程记录

Jenkins用maven风格build报错解决过程记录

1、Jenkins2.453新建项目&#xff0c;构建风格选的maven 2、自由风格构建部署没有任何问题&#xff0c;但是maven风格build一直失败&#xff0c;报错如下图 3、解决方案&#xff1a;在系统管理–系统配置–Maven项目配置&#xff0c;删除全局MAVEN_OPT的路径信息&#xff0c;…
阅读更多...
oracle 清空回收站

oracle 清空回收站

参考官方文档 select * from user_recyclebin; select * from dba_recyclebin; ---清除回收站中当前用户下的对象 purge recyclebin; ---清除回收站中所有的对象 purge dba_recyclebin; ---清除回收站中指定用户的表 PURGE TABLE owner.table_name; ---清除回收站中指…
阅读更多...
短信测压APP/网页

短信测压APP/网页

阅读更多...
PSCAD|应用于输电线路故障测距的行波波速仿真分析

PSCAD|应用于输电线路故障测距的行波波速仿真分析

1 主要内容 该程序参考文献《应用于输电线路故障测距的行波波速仿真分析》&#xff0c;利用线路内部故障产生的初始行波浪涌达线路两端测量点的绝对时间之差值计算故障点到两端测量点之间的距离&#xff0c;并利用小波变换得到初始行波波头准确到达时刻&#xff0c;从而精准定…
阅读更多...
HTML 入门 ( 一 )

HTML 入门 ( 一 )

HTML文档创建 首先创建一个txt文本文档 修改文件后缀 HTML标签 标签结构 标签又称为元素,是HTML的基本组成单位分为: 双标签与单标签推荐小写标签名 结构: 双标签示例代码: <marquee> My name is Kvein. </marquee>单标签示例代码: <input>标签的并列与嵌…
阅读更多...
AndroidStudio右下角显示内存使用情况

AndroidStudio右下角显示内存使用情况

目录 一.具体效果 二.4.0以下版本 三.4.0以上版本 四.增加内存配置 一.具体效果 二.4.0以下版本 1.打开 Android Studio. 2.进入设置界面。点击 Android Studio 左上角的“File”&#xff0c;然后选择“Settings” 3.在设置界面中&#xff0c;选择“Appearance & Beha…
阅读更多...
汇编语言与x64函数参数传递

汇编语言与x64函数参数传递

本节课学习视频&#xff1a;https://pan.quark.cn/s/429055967dfd 汇编语言作为编程语言与机器语言之间的桥梁&#xff0c;直接反映了硬件的工作方式。在不同的操作系统和硬件架构中&#xff0c;函数参数的传递方式可能有所不同。今天&#xff0c;我们将探讨x64位环境下函数参…
阅读更多...
KDD‘23 | AlphaMix: 高效专家混合框架（MoE）显著提高上证50选股表现

KDD‘23 | AlphaMix: 高效专家混合框架（MoE）显著提高上证50选股表现

KDD23 | AlphaMix: 高效专家混合框架&#xff08;MoE&#xff09;显著提高上证50选股表现 原创 QuantML QuantML 2024-04-18 09:17 上海 Content 本文提出了一个名为AlphaMix的新型三阶段专家混合&#xff08;Mixture-of-Experts&#xff0c;MoE&#xff09;框架&#xff0c;…
阅读更多...
c++使用spdlog库打日记

c++使用spdlog库打日记

打日记 打日志的本质就是多输出&#xff0c;c没有自带的日志库&#xff0c;只能使用第三方库实现&#xff0c;当然&#xff0c;直接cout输出也可以&#xff0c;但是一般日志库都进行了优化&#xff0c;比我们使用cout输出的效率更高&#xff0c;同时效果也更好&#xff0c;这里…
阅读更多...
正大国际：什么是庞氏骗局？

正大国际：什么是庞氏骗局？

在金钱的诱惑下&#xff0c;人性的贪婪与恐惧交织成一张无形的网&#xff0c;让无数人沉迷其中&#xff0c;无法自拔。这其中&#xff0c;庞氏骗局作为一种极具欺骗性的金融诈骗手段&#xff0c;更是将人们的贪婪与信任利用到了极致。那么&#xff0c;究竟什么是庞氏骗局呢&…
阅读更多...
1096 大美数

1096 大美数

solution B被A整除&#xff0c;B是A的倍数。B / AA整除B A把B整除 &#xff22;被A整除 B / A >n可以整除不同的四个因数之和 等价于 (a b c d) % n 0 #include<iostream> #include<cmath> using namespace std; int main(){int k, n, t;scanf("%d&q…
阅读更多...
基于TCC的分布式事务

基于TCC的分布式事务

优质博文&#xff1a;IT-BLOG-CN 一、分布式事务简介 分布式的架构中&#xff0c;分布式的事务是一个绕不过的挑战&#xff0c;微服务理念的流行让分布式的问题日益突出。 在公司内部&#xff0c; 笔者所接触的管理系统中实际上也存在着分布式事务。 这里假设有这三个系统&…
阅读更多...
Redis从入门到精通(二十二)Redis原理之数据结构、网络模型、通心协议、内存回收

Redis从入门到精通(二十二)Redis原理之数据结构、网络模型、通心协议、内存回收

文章目录 第8章 Redis原理8.1 Redis数据结构8.1.1 RedisObject8.1.2 动态字符串&#xff08;SDS&#xff09;8.1.3 string8.1.4 List8.1.5 Set8.1.6 ZSet8.1.7 Hash 8.2 Redis网络模型8.2.1 五种网络模型介绍8.2.1.1 用户空间和内核空间8.2.1.2 阻塞IO8.2.1.3 非阻塞IO8.2.1.4 …
阅读更多...
第二证券策略：股指预计维持震荡格局 关注金融、工程建设等板块

第二证券策略：股指预计维持震荡格局 关注金融、工程建设等板块

第二证券指出&#xff0c;一季度GDP同比增加5.3%&#xff0c;符合我们早前5%—5.5%的预测。边际上看&#xff0c;3月工业增加值、社零总额、出口同等比增速均显着回落&#xff0c;主要是1—2月阶段性提振因素衰退&#xff08;如闰年、集中假日、新年错位等&#xff09;以及去年…
阅读更多...
LeetCode in Python 200. Number of islands (岛屿数量)

LeetCode in Python 200. Number of islands (岛屿数量)

岛屿数量既可以用深度优先搜索也可以用广度优先搜索解决&#xff0c;本文给出两种方法的代码实现。 示例&#xff1a; 图1 岛屿数量输入输出示意图 方法一&#xff1a;广度优先搜索(bfs) 代码&#xff1a; class Solution:def numIslands(self, grid):if not grid:return 0…
阅读更多...
回应评论区剪映疑问

回应评论区剪映疑问

关于这篇文章 插件以及对应版本剪映重新打包整理&#xff1a; 链接&#xff1a;https://pan.baidu.com/s/1D2-pH1JhecGFxiTyFb6tGQ?pwd2k5n 提取码&#xff1a;2k5n 单独需要插件资源&#xff1a;链接&#xff1a;https://pan.baidu.com/s/1NsIyfAZTO3arnBzFdNBizQ?pwdri…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023