目录
- 图论
- 一、 图的基本概念和术语
- 二、图的存储结构
- 1. 数组(邻接矩阵)存储表示
- 无向图的数组(邻接矩阵)存储表示
- 有向图的数组(邻接矩阵)存储表示
- 邻接表存储表示
- 有向图的十字链表存储表示
- 无向图的邻接多重表存储表示
- 三、图的遍历算法
- 图的遍历——深度优先搜索(DFS)
- 图的遍历——广度优先搜索(BFS)
- 四、图的遍历算法的应用(无向图)
- 五、图的连通性问题
- 生成树
- Prim算法
- Kruskal 算法
图论
一、 图的基本概念和术语
网状结构,逻辑关系多对多
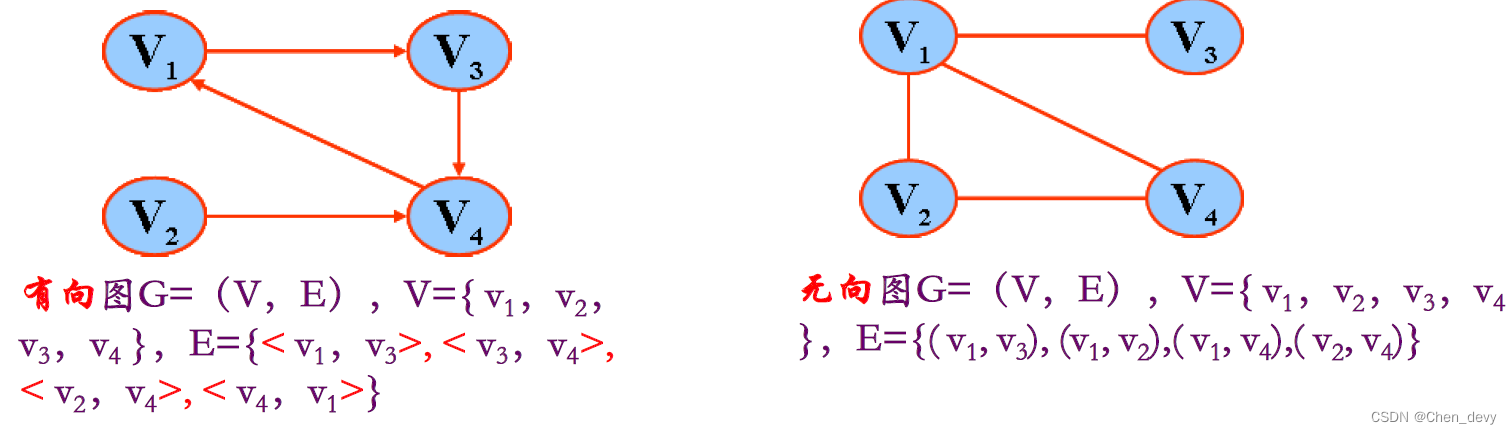
- 图:图G由集合V和E组成,记为G=(V,E)。图中的结点称为顶点,V(G)是顶点的非空有穷集;相关的顶点偶对称为边,E(G)是边的有穷集。
图分为有向图、无向图
- 有向图(Digraph)——V(G)是顶点的非空有限集;E(G)是有向边(即弧)的有限集合,弧是顶点的有序对,记<v, w>,v为弧尾(Tail),w为弧头(Head)
- 无向图(Undigraph)——V(G)是顶点的非空有限集;E(G)是边的有限集合,边是顶点的无序对,记(v, w)或(w, v),并且(v, w)=(w, v).
-
顶点:表示数据元素
-
边:表示数据元素之间的逻辑关系,分为有向边(顶点的有序对)和无向边(顶点的无序对)
-
网:边带权的无向图称作无向网;弧带权的有向图称作有向网。
-
完全图:n个顶点的含有 n(n-1)/2 条边的无向图称作完全图;n个顶点的含有 e=n(n-1) 条弧的有向图称作 有向完全图.
若边或弧的个数 e<nlogn,则称作稀疏图,否则称作稠密图。 -
邻接点、关联:假若顶点v 和顶点w 之间存在一条边,则称顶点v 和w 互为邻接点,边(v,w)和顶点v 和w相关联
-
度:无向图中和顶点v 关联的边的数目定义为v的度,记为TD(v)
有向图顶点的度分为入度和出度
■ 入度:有向图中以顶点v为弧头的弧的数目称为顶点v的入度,记为ID(v)
■ 出度:有向图中以顶点v为弧尾的弧的数目称为顶点v的出
度,记为OD(v) -
路径、路径长度:设无向图G=(V,E)中的一个顶点序列 u = v i , 0 , v i , 1 , … , v i , m = w { u=v_i,₀,v_i,₁, …, v_i, m=w} u=vi,0,vi,1,…,vi,m=w中,若 ( v i , j − 1 , v i , j ) ∈ E , 1 ≤ j ≤ m (v_{i, j-1},v_{i, j})∈E,1 ≤ j ≤ m (vi,j−1,vi,j)∈E,1≤j≤m,则称从顶点u 到顶点w 之间存在一条路径;路径上边的数目称作路径长度
■ 简单路径:序列中顶点不重复出现的路径
■ 简单回路:序列中第一个顶点和最后一个顶点相同的路径 -
连通图:若无向图G中任意两个顶点之间都有路径相通,则称此图为连通图。
-
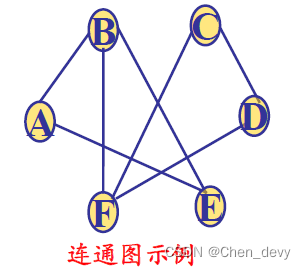
连通分量:若无向图为非连通图,则图中各个极大连通子图称作此图的连通分量。
-
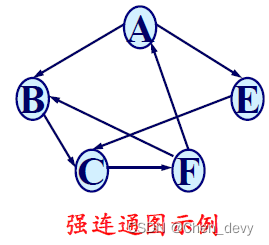
强连通图:有向图中若任意两个顶点之间都存在一条有向路径,则称此有向图为强连通图。否则,其各个极大强连通子图称作它的强连通分量。
-
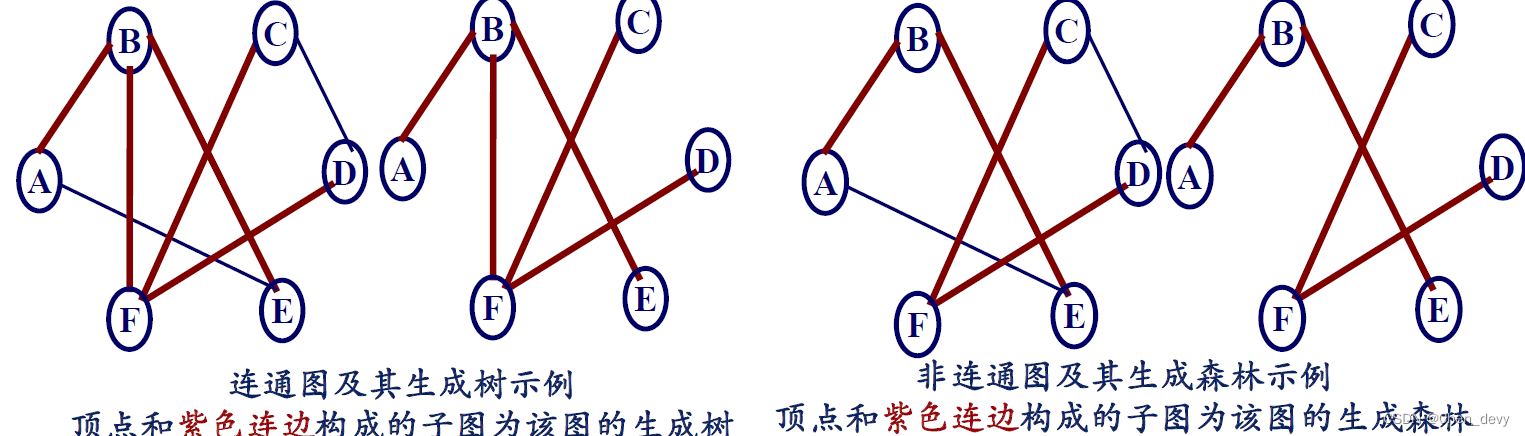
生成树:假设一个连通图有 n 个顶点和 e 条边,其中 n-1 条边和 n 个顶点构成一个极小连通子图,称该极小连通子图为此连通图的生成树。
-
生成森林:对非连通图,则称由各个连通分量的生成树的集合为此非连通图的生成森林。
-
有向树:如果一个有向图恰有1个顶点的入度为0,其余的顶点入度均为1,则称该图为一棵有向树
- 对于非强连通图的一个强连通分量:包含其全部n个顶点、n-1条弧、且只有1个顶点的入度为0、其余的顶点入度均为1的子图称为该连通分量的有生成向树.
- 对于非强连通图的所有强连通分量的有向生成树构成该有向图的生成森林.
- 一个有向图的生成森林由若干棵有向树组成,含有图中全部顶点,但只有足以构成若干棵不相交的有向树的弧.
二、图的存储结构
■ 图的存储表示(非顺序存储映像):
- 图的数组(邻接矩阵)存储表示
- 图的邻接表存储表示
- 有向图的十字链表存储表示
- 无向图的邻接多重表存储表示
■ 设计图的存储表示,应考虑方便以下操作:
• 求入度,出度
• 求邻接顶点
• 判断顶点之间是否有边相连
1. 数组(邻接矩阵)存储表示
无向图的数组(邻接矩阵)存储表示
■ n个顶点的图用2个数组存放:二维数组(
n
∗
n
n*n
n∗n的矩阵)存放顶点之间的逻辑关系(图中的边、弧),一维数组存放顶点信息(数据元素的值)
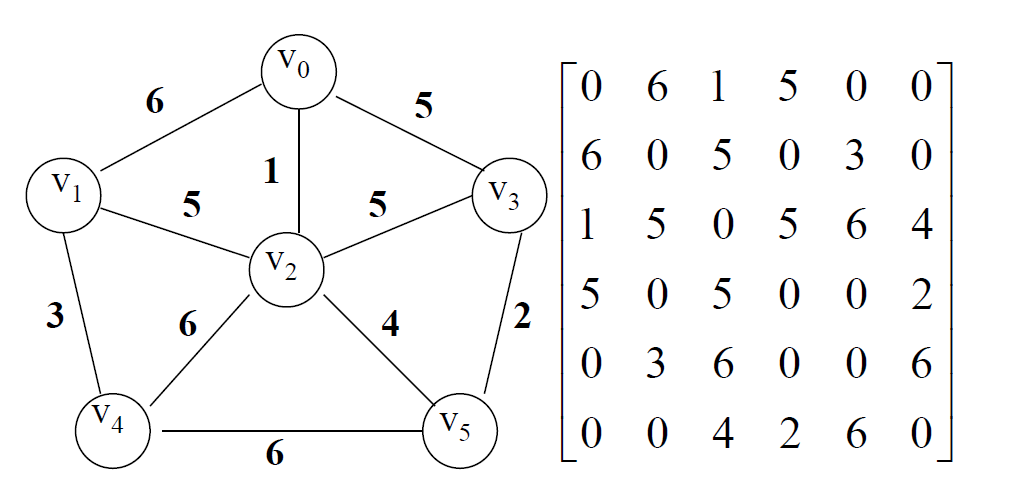
■ 设无向图
G
=
(
V
,
E
)
G=(V,E)
G=(V,E),A[i][j]表示顶点
v
i
v_i
vi 和
v
j
v_j
vj之间是否存在连边
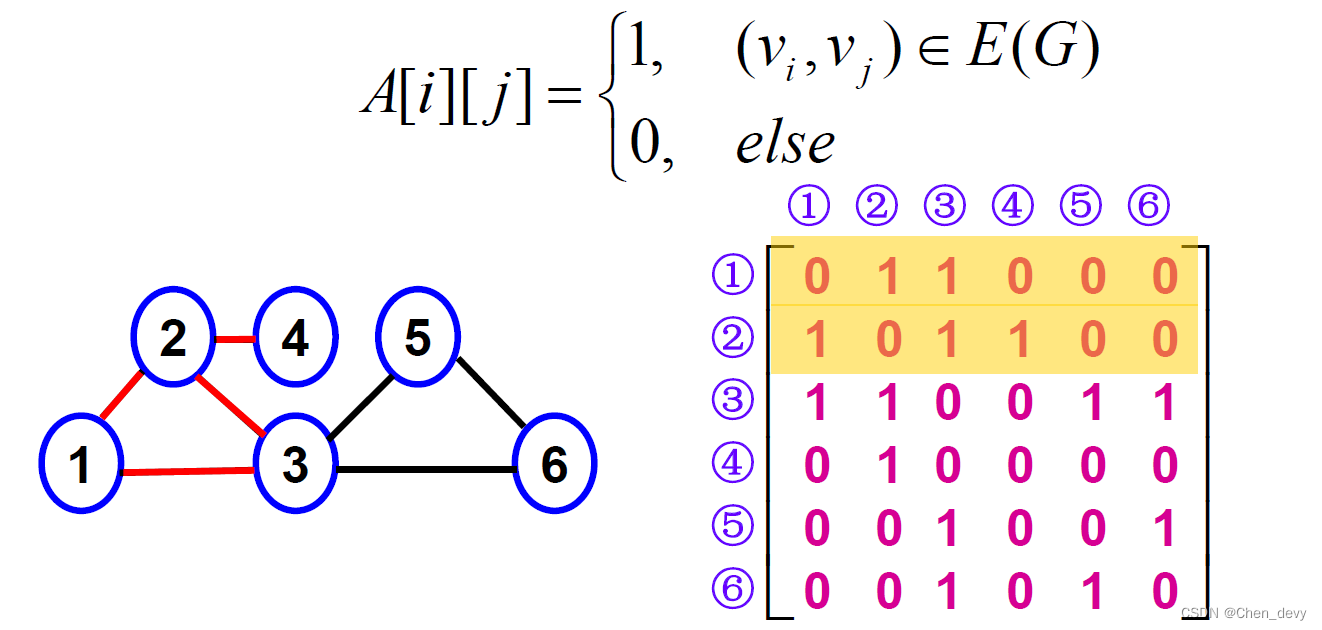
可以利用对称阵的压缩存储方法存储
无向图顶点
v
i
v_i
vi的度
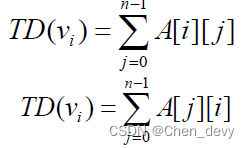
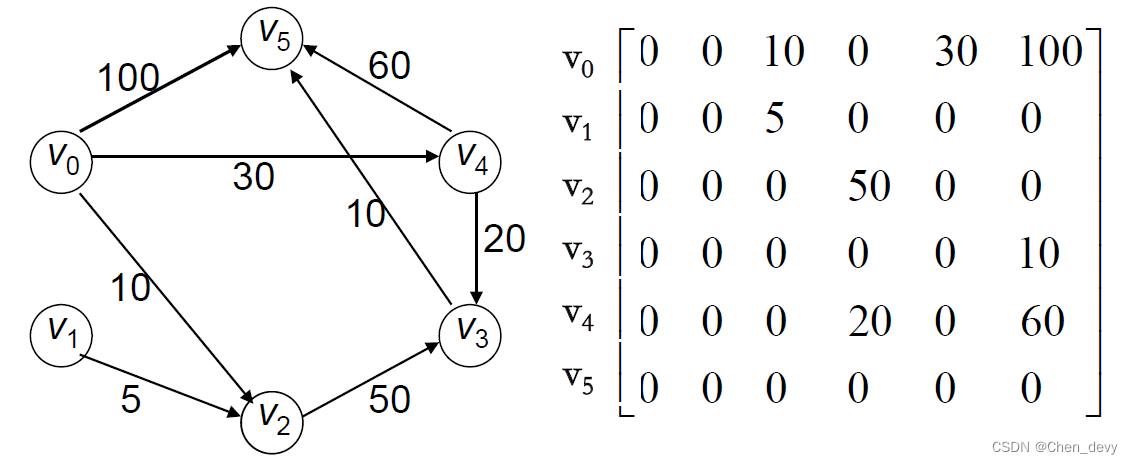
有向图的数组(邻接矩阵)存储表示
设有向图
G
=
(
V
,
E
)
G=(V,E)
G=(V,E), A[i][j]表示是否存在顶点
v
i
v_i
vi流向顶点
v
j
v_j
vj的弧.
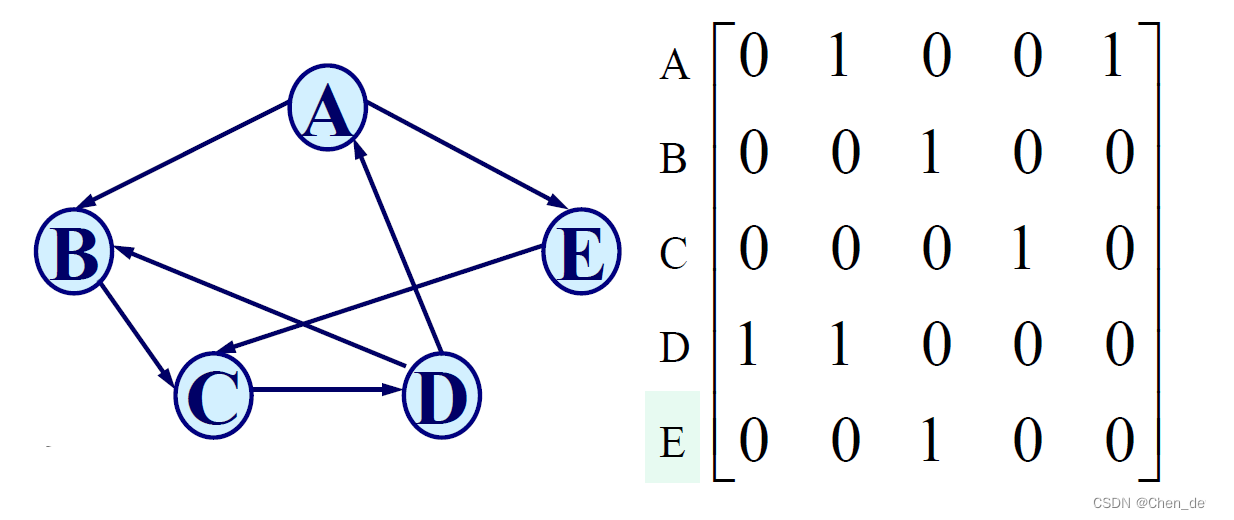
有向图邻接矩阵不一定是对称阵

无向网的邻接矩阵 w i j w_{ij} wij表示在顶点 v i v_i vi 和 v j v_j vj的连边上的权值。
有时:也用 ∞ ∞ ∞代表没有边有向网的邻接矩阵 w i j w_{ij} wij表示在顶点 v i v_i vi流向顶点 v j v_j vj的弧上的权值.
#define MAXSIZE 100
typedef struct {
VertexType vexs[MAXSIZE]; //一维数组存放顶点信息
int arcs[MAXSIZE][MAXSIZE];//邻接矩阵
int vexnum, arcnum; //顶点数和边数
int kind; //图的类型:有向图还是无向图
} MGraph;
MGraph T;
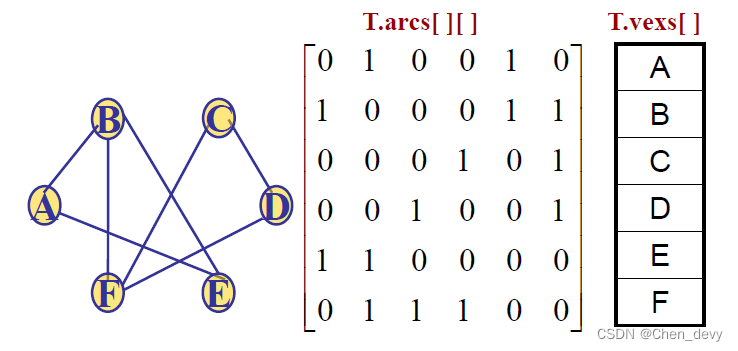
邻接表存储表示
无向图的邻接表:为顶点vi所建的单链表是将与顶点vi相关联 的边建成一个单链表;或者说:将顶点vi的邻接点建成一个单链表。
■ 图的一种链式存储结构,对图中每个顶点建立一个单链表,为顶
点
v
i
v_i
vi所建的单链表是将与顶点
v
i
v_i
vi相关联的边或弧建成一个单链表。
■ 用一维数组存放每个顶点的信息和相应单链表的头指针。
■ 每个数组元素存放图中一个顶点:顶点的数据(data)和为其所建单链表的头指针(firstarc)。
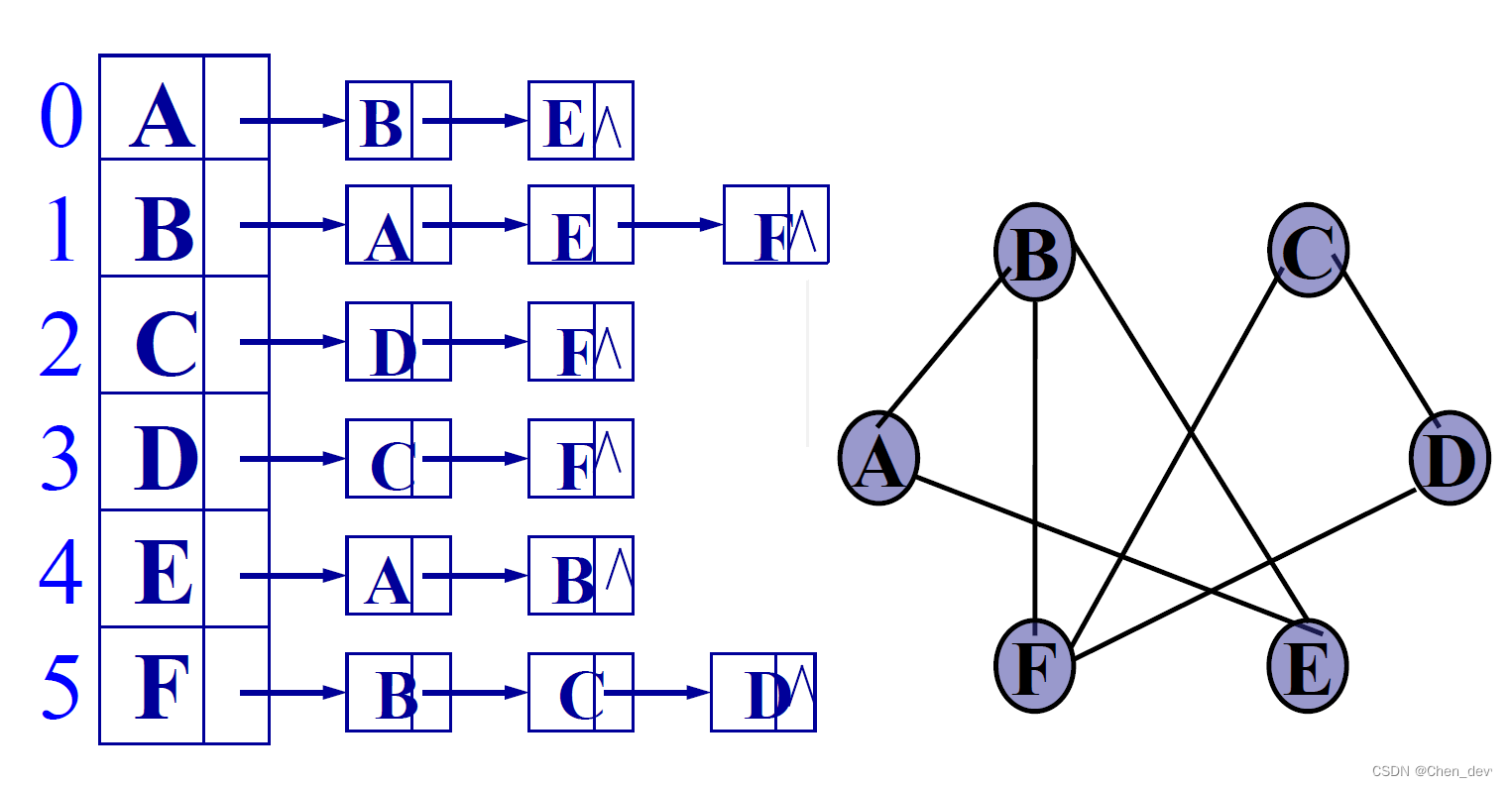
为便于维护数据的一致性,通常单链表中只要给出邻接点的存放位置----在一维数组中对应数组元素的下标即可
存的边数是2e个 ,也就是每个弧存了2次
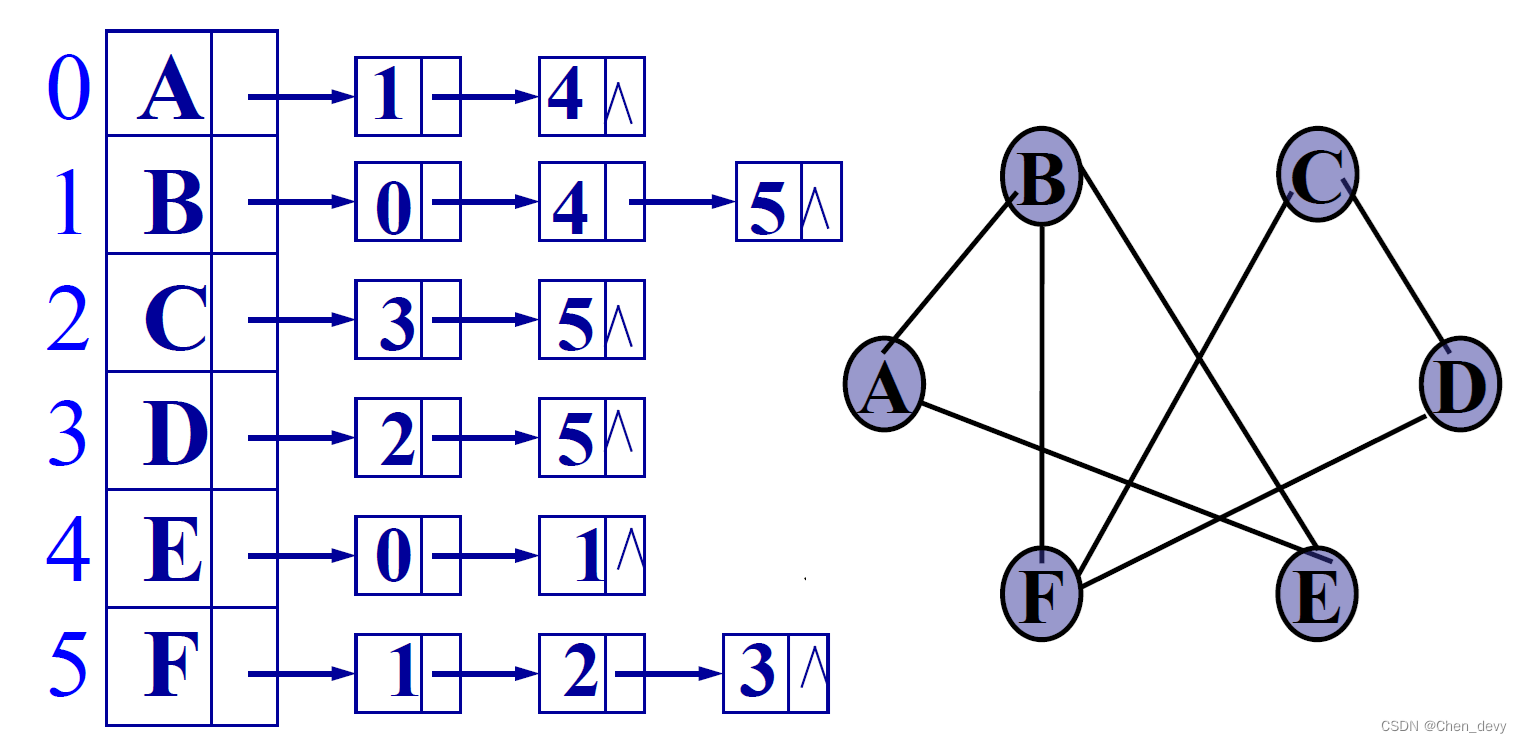
有向图的邻接表:第i个单链表(为
v
i
v_i
vi所建单链表)中的结点是从顶点
v
i
v_i
vi流出的弧流向的顶点
顶点vi的出度是第i个单链表中含有的数据元素的个数,即为vi所建单链表的长度。
在有向图的邻接表中不易找到指向该顶点的弧。
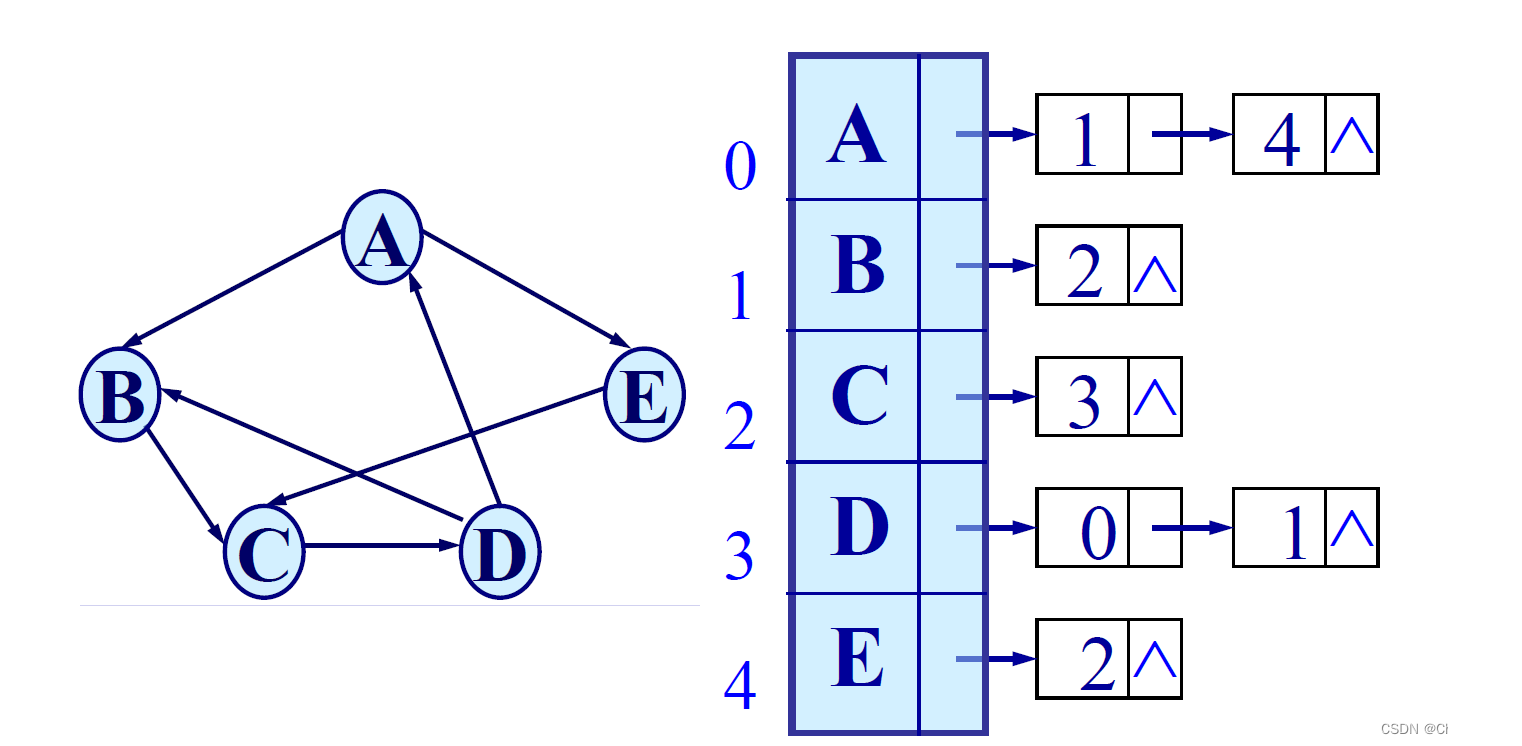
typedef struct ArcNode {
int vex; // 该弧所指向的顶点的位置
struct ArcNode *link; // 指向下一条弧的指针
InfoType *info; // 该弧相关信息的指针
}ArcNode;//单链表节点类型
typedef struct VNode {
int data; // 顶点信息
ArcNode *firstarc; // 指向第一条依附该顶点的弧
}VNode;//数组元素类型
typedef struct {
VNode arc[MAXSIZE];
int vexnum, arcnum;
int kind; //表示有向图还是无向图
}Graphs;
逆向:
有向图的逆邻接表中,为顶点vi建的单链表示流向该顶点的弧
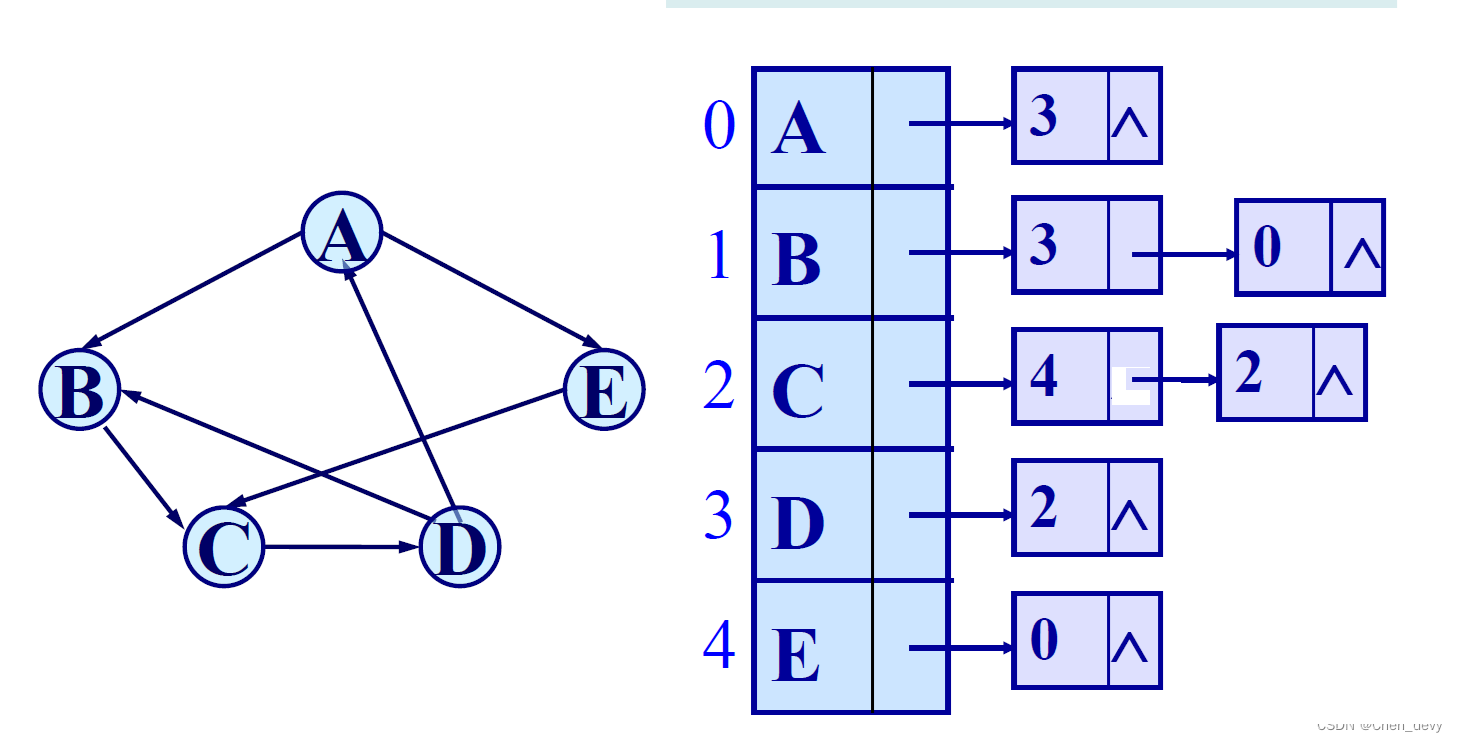
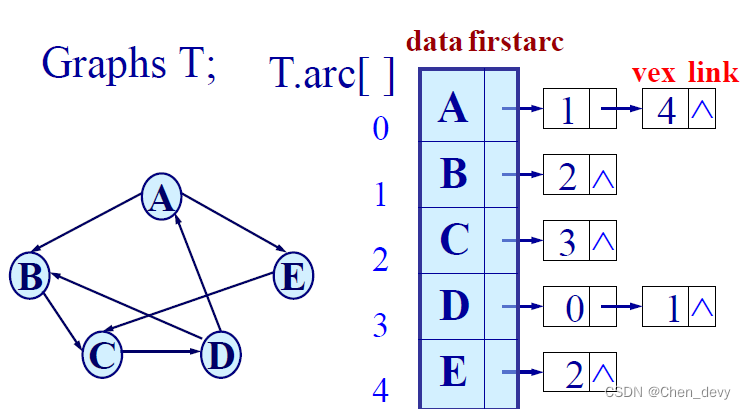
网的邻接表表示
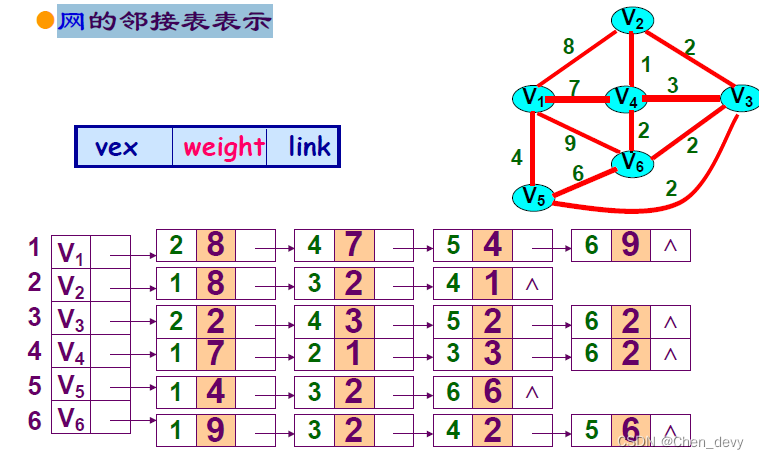
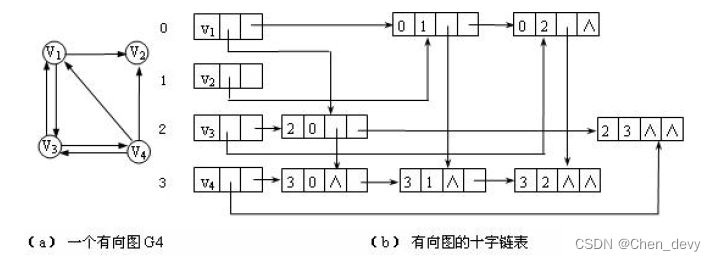
有向图的十字链表存储表示
每个顶点建2个单链表:流出去的弧建一个单链表,流入的弧建一个单链表。

typedef structArcBox { // 弧的结构表示
int tailvex, headvex;
InfoType *info;//注意定义的类型
struct ArcBox *hlink,*tlink;
}ArcBox;
typedef structVexNode { // 顶点的结构表示
int data;
ArcBox *firstin,*firstout;
}VexNode;
typedef struct {
VexNode xlist[MAXSIZE]; // 顶点信息
int vexnum, arcnum; //有向图的当前顶点数和弧数
}OLGraph;
无向图的邻接多重表存储表示

边的结构表示
typedef struct Ebox {
int mark;
int ivex, jvex;
struct EBox *ilink, *jlink;
} EBox;
三、图的遍历算法
图的遍历:从图中某个顶点出发访遍图中其余顶
点,并且使图中的每个顶点仅被访问一次的过程
遍历应用举例:
- 判断图的连通性、
- 求等价类等
- 求连通分量
- 求路径相通
深度优先搜索和广度优先搜索
图的遍历——深度优先搜索(DFS)
- 图的存储——邻接矩阵和邻接表均可以
- 判别图中的顶点v的邻接点是否被访问的方法:
⮚ 解决的办法:为每个顶点设立一个“访问标志”,设一维数组visited[ ],
① visited[v]=1表示顶点v已经被访问
② visited[v]=0表示顶点v尚未被访问
③ 初始化时,所有顶点均为未被访问
- 深度优先搜索生成树:访问时经过的顶点和边构成 的子图
- 深度优先搜索生成森林:若选用多个出发点做深度优先搜索,会产生多棵深度优先搜索生成树—构成深度优先搜索生成森林.
深度优先搜索遍历连通图的过程类似于树的先根遍历`
深度优先搜索应用:
判断无向图是否连通?
若从无向图中任一点出发能访问到图中所
有顶点,则该图为连通图
判断有向图是否强连通?
若从有向图中每一点出发能访问到图中所有顶点,则该图为强连通图.
实现方法:
以邻接表为例实现图的深度优先搜索
存储结构为:
typedef struct ArcNode {
int vex; // 该弧所指向的顶点的位置
struct ArcNode *link; // 指向下一条弧的指针
InfoType *info; // 该弧相关信息的指针
} ArcNode;//单链表节点类型
typedef struct VNode {
int data; // 顶点信息
ArcNode *firstarc; // 指向第一条依附该顶点的弧
} VNode;//数组元素类型
typedef struct {
VNode arc[MAXSIZE];
int vexnum, arcnum;
int kind; //表示有向图还是无向图
} Graphs;
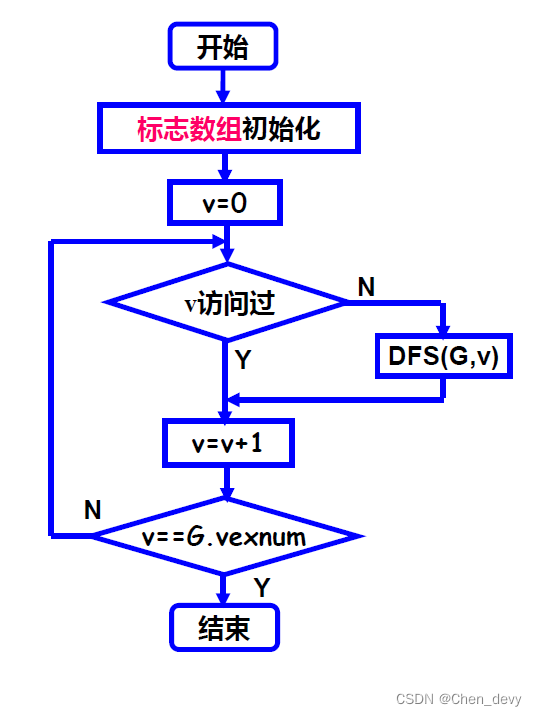
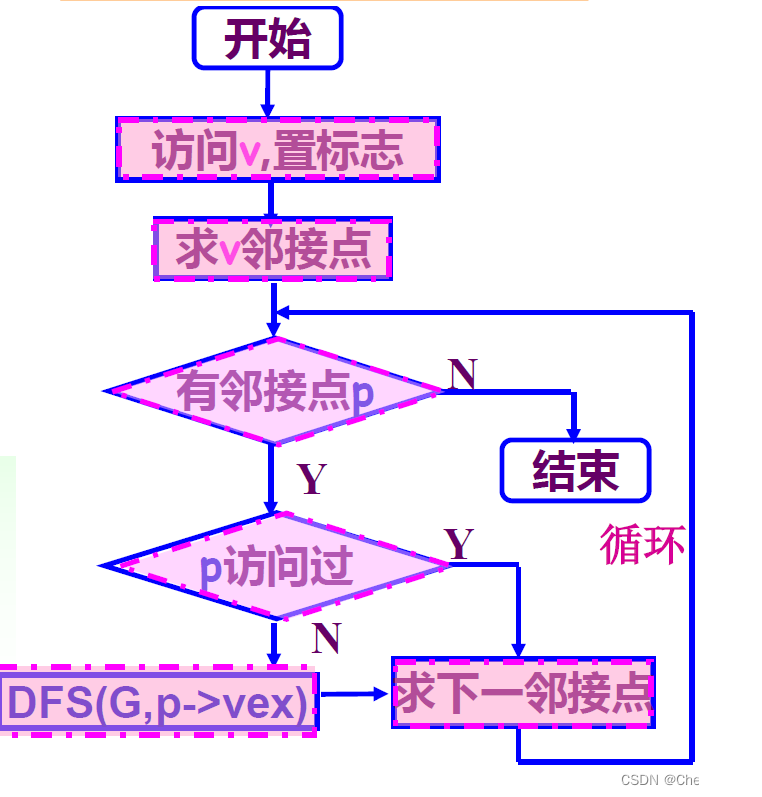
DFS实现流程图以及代码:
typedef struct ArcNode {
int vex; // 该弧所指向的顶点的位置
struct ArcNode *link; // 指向下一条弧的指针
InfoType *info; // 该弧相关信息的指针
} ArcNode;//单链表节点类型
typedef struct VNode {
int data; // 顶点信息
ArcNode *firstarc; // 指向第一条依附该顶点的弧
} VNode;//数组元素类型
typedef struct {
VNode arc[MAXSIZE];
int vexnum, arcnum;
int kind; //表示有向图还是无向图
} Graphs;
//深度优先搜索
void DFSTraverse(Graphs G){
for(int v=0;v<G.vexnum;++v){
visited[v]=0;
for(v=0;v<G.vexnum;++v){
if(!visited[v])
DFS(G,v);
}
}
}
void DFS(Graphs G,int v){
printf("%d\t",v);
visited[v]=1;
p=G.arc[v].firstarc;
while(p){
w=p->vex;
if(visited[w]==0)
DFS(G,w);
p=p->link;
}
}
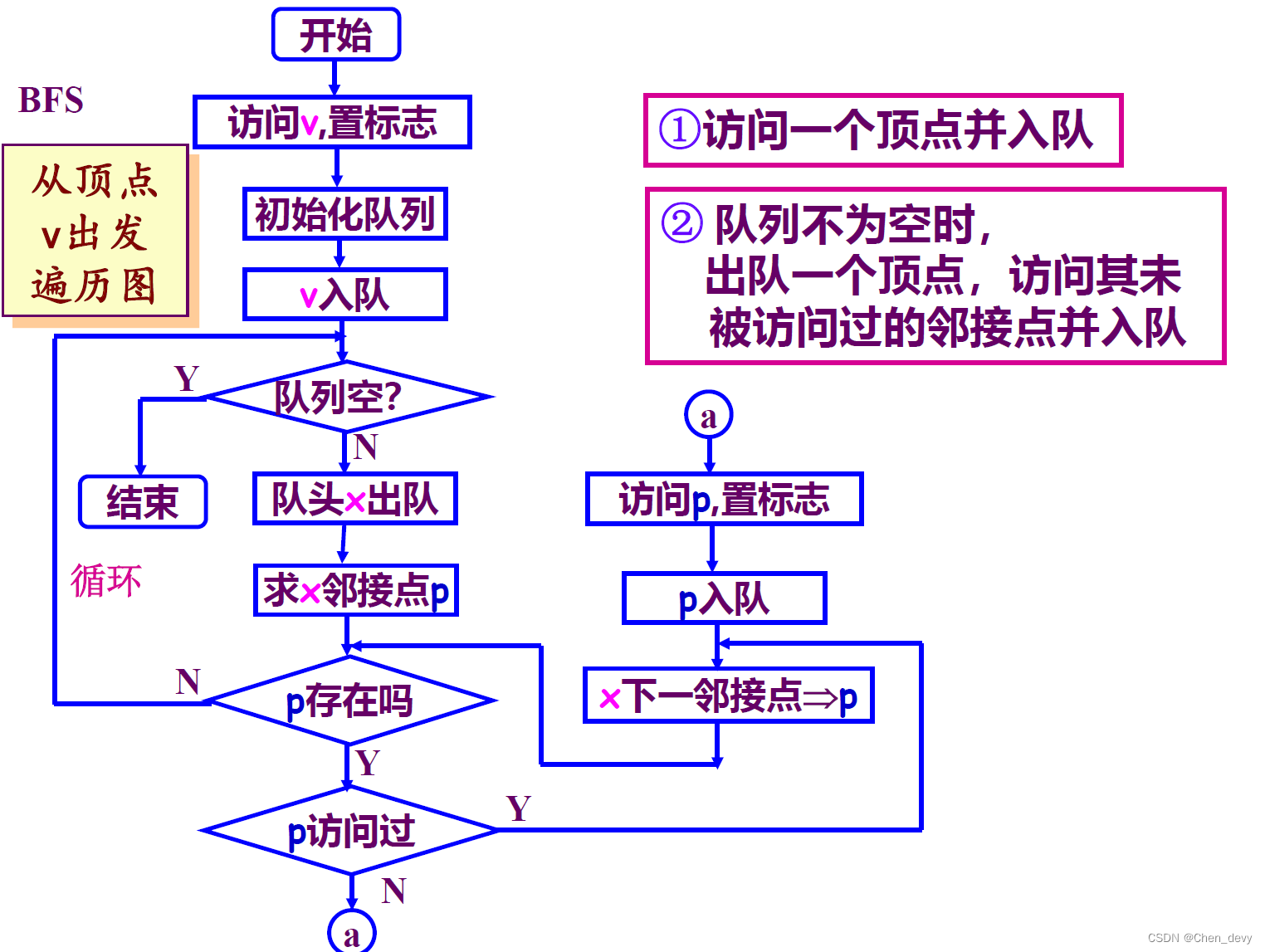
图的遍历——广度优先搜索(BFS)
■ 广度优先搜索生成树:访问时经过的顶点和边构成的子图。
■ 广度优先搜索生成森林:选用多个出发点做广度优先搜索,会产生多棵广度优先搜索生成树—构成广度优先搜索生成森林。
■ 对连通图,从起始点v到其余各顶点必定存在路径。按此路径长度递增次序访问。
int visited[Max];
void BFSTraverse(Graphs G){
for(v=0; v<G.vexnum; ++v) visited[v] = 0;
for( v=0; v<G.vexnum; ++v )
if(!visited[v])
BFS(G, v);
}
void BFS(Graphs G,int v){
int Q[MAX],f=0,r=0;
printf("%d\t",w);
visited[v]=1;
Q[r++]=v;
while(f<r){
x=Q[f++];
p=G.arc[x].firstarc;
while(p){
w=p->vex;
if(visited[w]==0){
visited[w]=1;
printf("%d\t",w);
Q[r++]=w;
}
p=p->link;
}
}
}
最小生成树
四、图的遍历算法的应用(无向图)
(待补充)
求两个点之间的最短路径
求两个顶点之间的简单路径
直接使用深度优先搜索还不太行 需要先处理一下
遍历应用举例:
- 判断图的连通性、
- 求等价类等
- 求连通分量
- 求路径相通
五、图的连通性问题
生成树的存放方式:
- 孩子兄弟表示法
- 双亲表示法
⮚ 若从无向图中任一点出发采用深度优先搜索或广度优先搜索能访问到图中所有顶点,则该图为连通图,否则为非连通图
对连通图:深度优先搜索或广度优先搜索访问时经过的顶点和边构成的子图称为深度优先搜索生成树或广度优先搜索生成树
对非连通图:深度优先搜索或广度优先搜索访问时经过的顶点和边构成的子图称为深度优先搜索生成森林或广度优先搜索生成森林
生成树
生成树 子图 连通的子图
■ 生成树:假设一个连通图有 n 个顶点和 e 条边,其中 n-1
条边和 n 个顶点构成一个极小连通子图,称该极小连通子图为此连通图的生成树。
生成森林:对非连通图,则称由各个连通分量的生成树的集合为此非连通图的生成森林。
最小生成树 带权图的生成树上的各边权值之和 称为这棵树的代价。最小代价生成树是各边权值总和最小的生成树
最小生成树的性质(MST性质) 采用深度优先搜索 或 广度优先搜索 求? 不太行
贪心策略 不一定是最优解 但在生成最小生成树的时候 是适用的 Prim普利姆算法 Kruscal算法
具有MST性质 就是最小生成树
MST性质(最小生成树性质): 令G=(V, E,
W)为一个带权连通图,T为G的一生成树。对任一不在T中的边uv,如果将uv加入T中会产生一回路,使得uv是回路中权值最大的边。那么树T具有MST性质。
Prim算法
图采用邻接矩阵和邻接表存放均可。下面以邻接矩阵为例实现prim算法
define MAX 100
define MAXEDGE 1000000
typedef struct{
int arcs[MAX][MAX];
int vexnum,arcnum;
}AGraphs;
Prim算法代码示例:
define MAX 100
define MAXEDGE 1000000
typedef struct{
int arcs[MAX][MAX];
int vexnum,arcnum;
}AGraphs;
typedef struct{
int adjvex;
int lowcost;
}EdgeType;
/*
当顶点v尚未加入生成树时,closedge[v]存放的是v与生成树中的顶点相连的最好情况:v与生成树中的顶点的所有连边中权值最小的那条边;closedge[v].adjvex存放的这条权值最小的边的另一个顶点,closedge[v].lowcost存放的这条权值最小的边的权值
如何区分生成树中的顶点和不在生成树中的顶点呢?
closedge[w].lowcost==0表示w已经加入生成树
*/
void prim(AGraphs G,int u){
int i,j,k;
EdgeType closedge[MAX];
for(j=0;j<G.vexnum;j++){
closedge[j].adjvex=u;
closedge[j].lowcost=G.arcs[u][j];
}
closedge[u].lowcost=0;
for(i=1;i<G.vexnum;i++){
k=minclosedge(closedge);
printf("(%d,%d)", closedge[k].adjvex,k);
closedge[k].lowcost=0;
for(j=0;j<G.venum;j++)
if(G.arcs[k][j]< closedge[j].lowcost){
closedge[j].lowcost= G.arcs[k][j];
closedge[j].adjvex =k;
}
}
}
int minclosedge(EdgeType closedge[]){
int min,j,k; min=MAXEDGE; k=-1;
for(j=0;j<G.vexnum;j++)
if(closedge[j]. lowcost !=0&&closedge[j].lowcost<min){
min=closedge[j]. lowcost; k=j;
}
return k;
}
//时间复杂度:O(n2) Prim算法适合于稠密图
问法
最小生成树的求解过程
文字叙述 画表 求解过程
伪码描述(上述程序)
Kruskal 算法
先排序
对所有边按照权值升序排序
从小开始加 只要不产生回路
最后加到
n
−
1
n-1
n−1
需要 排序(适合于吸收图)
Kruscal算法适合稀疏图,时间复杂度为O(eloge),e为图的边数,因为该算法要对边按照权值排序,(堆、快速。归并)排序算法的平均时间复杂度O(eloge)
![Amazon云计算AWS之[1]基础存储架构Dynamo](https://img-blog.csdnimg.cn/direct/0bd82ce343354d1a9881ebbfd7443378.png#pic_center)