Focal Loss用来解决正负样本不平衡问题,并提升训练过程对困难样本的关注。
在一阶段目标检测算法中,以YOLO v3为例,计算置信度损失(图中第3、4项)时有目标的点少,无目标的点多,两者可能相差百倍千倍甚至更多,这就导致无目标的置信度损失会以压倒性的数量优势在数值上淹没有目标的置信度损失。
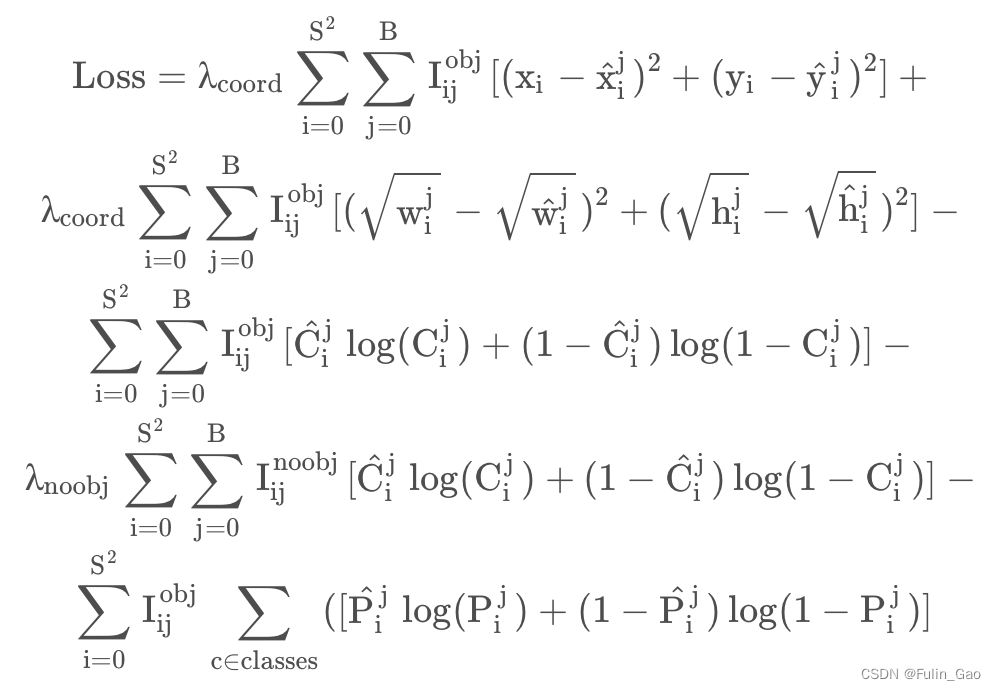
首先,我们回顾一下第三、四项里 [ ⋅ ] [\cdot] [⋅]所对应的BCELoss,其公式如下:

其中, p ∈ [ 0 , 1 ] p\in[0,1] p∈[0,1]是经sigmoid输出的预测概率, y ∈ { 0 , 1 } y\in\{0,1\} y∈{0,1}是真实标签。简单起见,我们使用 p t p_t pt简化上述损失, p t p_t pt公式如下:
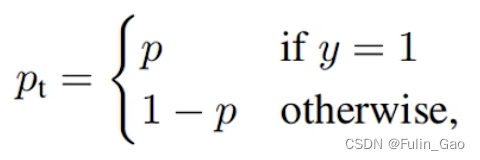
于是,我们得到

在此基础上,Focal Loss引入 α t \alpha_t αt来加权BCELoss以解决正负样本不平衡的问题,公式如下:
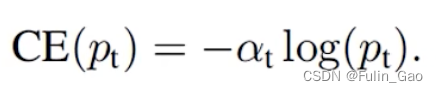
其中, α t \alpha_t αt定义如下:
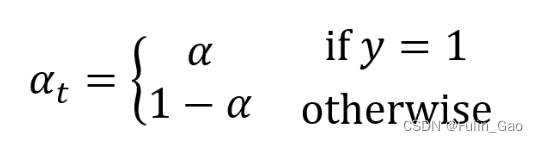
其中, α ∈ [ 0 , 1 ] \alpha\in[0,1] α∈[0,1]是自行设定的权重参数。直观来说,当正样本较少时,我们可以设定一个较大的 α \alpha α,例如 0.9 0.9 0.9,这样正样本的损失相比负样本的损失就会更大从而解决正负样本失衡的问题。
⚠️ 事实上,Focal Loss原文中的最佳 α \alpha α是 0.25 0.25 0.25,这说明原文并不是用它来处理正负样本失衡的,更像是一个超参数。
进一步地,Focal Loss还能使得模型在训练过程中更加关注困难样本。对于正样本来说,我们希望预测概率 p → 1 p\rightarrow 1 p→1,那么 p p p越小说明该样本预测起来就越困难,反之就越简单。对于负样本, p p p越小说明该样本预测起来就越简单,反之就越困难。直观上,我们只需努力矫正困难样本,毕竟简单样本已经预测的不错了,于是Focal Loss引入 ( 1 − p t ) γ (1-p_t)^{\gamma} (1−pt)γ来加权BCELoss以实习对困难样本的关注,公式如下:
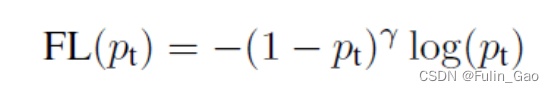
其中, γ ≥ 0 \gamma\geq0 γ≥0,从下表可以看出, ( 1 − p t ) γ (1-p_t)^{\gamma} (1−pt)γ使简单样本的损失大大降低,从而使困难样本与简单样本的损失比增大,以使训练过程更加关注困难样本。
| y y y | γ \gamma γ | p p p | p t p_t pt | C E ( p , y ) CE(p,y) CE(p,y) | ( 1 − p t ) γ (1-p_t)^{\gamma} (1−pt)γ | F L ( p t ) FL(p_t) FL(pt) |
|---|---|---|---|---|---|---|
| 1 | 2 | 0.9 | 0.9 | 0.11 | 0.01 | 0.0011 |
| 1 | 2 | 0.1 | 0.1 | 2.30 | 0.81 | 1.863 |
| 0 | 2 | 0.2 | 0.8 | 0.22 | 0.04 | 0.0088 |
| 0 | 2 | 0.8 | 0.2 | 1.61 | 0.64 | 1.0304 |
综合 α t \alpha_t αt和 ( 1 − p t ) γ (1-p_t)^{\gamma} (1−pt)γ即为完整的Focal Loss,公式如下:
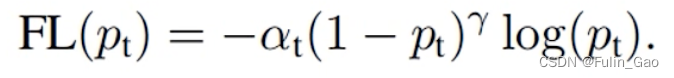
写成
p
p
p和
α
\alpha
α的形式就是:
F
L
(
p
)
=
{
−
α
(
1
−
p
)
γ
log
(
p
)
,
i
f
y
=
1
−
(
1
−
α
)
p
γ
log
(
1
−
p
)
,
o
t
h
e
r
w
i
s
e
FL(p)=\begin{cases}-\alpha(1-p)^{\gamma}\log(p),&if~y=1\\-(1-\alpha)p^{\gamma}\log(1-p), &otherwise\end{cases}
FL(p)={−α(1−p)γlog(p),−(1−α)pγlog(1−p),if y=1otherwise
致谢:
本博客仅做记录使用,无任何商业用途,参考内容如下:
3.1 YOLO系列理论合集(YOLOv1~v3)