1、 简介
在神经网络中,激活函数扮演着至关重要的角色。它们的主要目的是引入非线性因素,使得网络能够学习和表示更加复杂的函数映射。以下是激活函数应具备的特点,以及这些特点为何重要的详细解释:
-
引入非线性有助于优化网络:
非线性激活函数是神经网络能够解决非线性问题的关键。如果没有非线性激活函数,无论神经网络有多少层,最终都相当于一个线性模型,这大大限制了网络的表达能力。非线性激活函数使得神经网络可以通过叠加多个非线性层来学习复杂的数据分布和模式。例如,ReLU(Rectified Linear Unit)激活函数通过将所有负值置为零,引入了非线性,同时保持了计算的简单性。 -
不要过度增加计算成本:
激活函数需要在每次前向传播和反向传播时被计算,因此它们应该尽可能简单,以避免不必要的计算开销。复杂的激活函数可能会导致计算成本显著增加,从而影响网络的训练效率。例如,Sigmoid函数虽然引入了非线性,但其计算成本相对较高,并且在反向传播时可能导致梯度消失问题,因此在现代神经网络中使用较少。 -
不妨碍梯度流动:
梯度流动是神经网络训练中的核心机制,它允许网络通过调整权重来最小化损失函数。如果激活函数导致梯度消失(例如,梯度接近于零),那么网络将难以学习。理想的激活函数应该能够保持梯度的流动,使得网络在训练过程中能够有效地学习。ReLU激活函数在这方面表现良好,因为它的梯度在正区间是恒定的,从而避免了梯度消失问题。 -
保持数据分布:
激活函数还应该有助于保持数据的分布特性,使得网络能够更好地学习数据的内在结构。例如,某些激活函数可能会使得输出数据分布变得不均匀,这可能会影响网络的泛化能力。而像Leaky ReLU或Parametric ReLU(PReLU)这样的激活函数,通过允许一小部分负梯度流动,可以在一定程度上保持数据分布的多样性。
2. 激活函数的演变
线性函数
y
=
c
x
y = cx
y=cx(其中
c
c
c 是一个常数)是一种非常基础的激活函数。当
c
=
1
c = 1
c=1 时,它简化为身份函数,即
y
=
x
y = x
y=x,这个函数仅仅将输入
x
x
x 直接传递到输出
y
y
y,不进行任何变换。

2.1.对数西格玛双曲切线系列
L
o
g
i
s
t
i
c
S
i
g
m
o
i
d
(
x
)
=
1
1
+
e
−
x
{\mathrm{Logistic~Sigmoid}}\left(x\right)={\frac{1}{1+e^{-x}}}
Logistic Sigmoid(x)=1+e−x1
T
a
n
h
(
x
)
=
e
x
−
e
−
x
e
x
+
e
−
x
\mathrm{Tanh}(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}
Tanh(x)=ex+e−xex−e−x
以上两个函数是早期流行的非线性激活函数,其灵感来自于生物意义上的神经元(注意:生物神经元遵守全有或全无的定律,所以它们的输出只有0或1,中间没有任何东西)。Logistic Sigmoid将输出限制在[0,1],但输出相对于输入的大小变化不大(饱和的输出),造成梯度损失。它也不适合于优化,因为输出不是以零为中心的。
相比之下,Tanh(x)是0中心的,其输出为[−1,1];然而,梯度消失的问题仍未解决[−1,1].
2.2. ReLU系列
整流线性单元(ReLU)由于其简单性和改进的性能,已经成为激活函数的最先进(最高质量、最高性能、SOTA)。

R
e
L
U
(
x
)
=
m
a
x
(
0
,
x
)
=
{
x
,
i
f
x
≥
0
0
,
o
t
h
e
r
w
i
s
e
\mathrm{ReLU}(x)=\mathrm{max}(0,x)=\left\{\!\!\begin{array}{l l}{{x,}}&{{\mathrm{if}\;x\geq0}}\\ {{0,}}&{{\mathrm{otherwise}}}\end{array}\right.
ReLU(x)=max(0,x)={x,0,ifx≥0otherwise
然而,ReLU有一个负值投入利用不足(under-utilisation)的问题。
2.3. 指数单位系列
Logistic Sigmoid和Tanh的问题是饱和输出,即对于从无限小到无限大的输入范围来说,输出的狭窄性([0,1]),加上ReLU不能很好地利用负输入。这就是指数线性单元(ELU)被发现的地方。

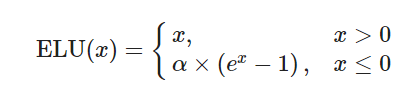
2.4学习和适应系统
到目前为止,提到的Sigmoid、Tanh、ReLU和ELU系统的激活函数都是人工设计的,可以说,可能没有充分提取数据的复杂性。
APL(x)=max(0,x)+S∑s=1asimax(0,−x+bsi)

在APL中,ai和bi是学习参数,激活函数本身也会发生变化(注意:S=3和S=4的图看起来是一样的,但仔细观察它们是不同的)。
2.5 其他。
现在已经提出了许多其他激活函数,包括Softplus函数、随机函数、多项式函数、核函数等等。.

上表总结了这些优点和缺点,从左到右的项目是:梯度损失、非线性、优化困难、缺乏适应性和计算成本。下表总结了该系统的优点和缺点。
3.基于Logistic Sigmoid/Tanh的激活函数。
针对operatornameTanh(x) 的狭窄输出范围和梯度消失问题,提出了一个缩放的双曲切线(sTanh)。
o p e r a t o r n a m e s T a n h ( x ) = A × o p e r a t o r n a m e T a n h ( B × x ) operatornamesTanh(x)=A×operatornameTanh(B×x) operatornamesTanh(x)=A×operatornameTanh(B×x)
提出了参数化的sigmoid函数是一个可微调的、连续的有界函数。
o
p
e
r
a
t
o
r
m
e
P
S
F
(
x
)
=
(
1
1
+
e
x
p
(
−
x
)
)
m
o p e r a t o r m e P S F(x)=(\frac{1}{1+e x p(-x)})^{m}
operatormePSF(x)=(1+exp(−x)1)m
同样,有人提出了移位的对数西格玛和整流的双曲正割,但输出饱和和梯度消失的问题仍然存在。提出了按比例的sigmoid和惩罚的Tanh,但梯度消失是不可避免的。
后来,有人提出了一种叫做噪声激活函数的方法,即给激活函数一个随机数以改善梯度流动,成功地处理了饱和输出问题。Hexpo函数也解决了大部分的梯度消失问题。
H
e
x
p
o
(
x
)
=
{
−
a
×
(
e
−
x
/
b
−
1
)
,
x
≥
0
c
×
(
e
x
/
d
−
1
)
,
x
<
0
\mathrm{Hexpo}(x)=\left\{\begin{array}{l l}{{-a\times\left(e^{-x/b}-1\right),}}&{{x\geq0}}\\ {{c\times\left(e^{x/d}-1\right),}}&{{x\lt 0}}\end{array}\right.
Hexpo(x)={−a×(e−x/b−1),c×(ex/d−1),x≥0x<0

同时提出了sigmoid加权线性单元(SiLU)和改进的logistic sigmoid(ISigmoid),并解决了饱和输出和梯度消失问题。这同样适用于线性缩放双曲切线(LiSHT)、艾略特和软根信号(SRS)。
Sigmoid/Tanh系统中的许多激活函数都试图克服梯度消失问题,但在许多情况下,这个问题并没有得到完全解决。
4. 整流的激活功能
整流线性单元(ReLU)是一个简单的函数,对于正的输入,它输出一个恒定的函数,对于负的输入,输出为零(输入为零时,输出也为零)。
R
e
L
U
(
x
)
=
{
x
,
i
f
x
≥
0
0
,
o
t
h
e
r
w
i
s
e
{\mathrm{ReLU}}(x)={\left\{\begin{array}{l l}{x,}&{{\mathrm{if~}}x\geq0}\\ {0,}&{{\mathrm{otherwise}}}\end{array}\right.}
ReLU(x)={x,0,if x≥0otherwise
因此,导数值只能是1(正输入)或0(负输入),所以Leaky ReLU(LReLU)被修改为对负输入返回一个小值而不是0。Leaky ReLU (LReLU)已被修改为对负输入返回一个小值而不是0。
L
R
e
L
U
(
x
)
=
{
x
,
x
≥
0
0.01
×
x
,
x
<
0
{\mathrm{LReLU}}(x)={\left\{\begin{array}{l l}{x,}&{x\geq0}\\ {0.01\times x,}&{x\lt 0}\end{array}\right.}
LReLU(x)={x,0.01×x,x≥0x<0
然而,LReLU的问题是它不知道0.01是否是正确的系数,而参数ReLU(PReLU)通过学习系数避免了这个问题。
P
R
e
L
U
(
x
)
=
{
x
,
x
≥
0
p
×
x
,
x
<
0
{\mathrm{PReLU}}(x)={\left\{\begin{array}{l l}{x,}&{x\geq0}\\ {p\times x,}&{x\lt 0}\end{array}\right.}
PReLU(x)={x,p×x,x≥0x<0
然而,PReLU的缺点是容易出现过度学习。
R
R
e
L
U
(
x
)
=
{
x
,
x
≥
0
R
×
x
,
x
<
0
\mathrm{RReLU}(x)=\left\{\begin{array}{l l}{{x,}}&{{x\geq0}}\\ {{R\times x,}}&{{x\lt 0}}\end{array}\right.
RReLU(x)={x,R×x,x≥0x<0
随机化ReLU(RReLU)是一种随机选择系数的方法。

(注:系数非常小,几乎是重叠的)

已经提出了ReLU的各种其他变种。
指数激活函数
指数系统的激活函数解决了ReLU中的梯度消失问题。
E
L
U
(
x
)
=
{
x
,
i
f
x
>
0
α
×
(
e
x
−
1
)
,
o
t
h
e
r
w
i
s
e
\mathrm{ELU(x)}=\left\{\!\!\begin{array}{c c}{{x,}}&{{\mathrm{if}\,x\gt 0}}\\ {{\alpha\times\left(e^{x}-1\right),}}&{{\mathrm{otherwise}}}\end{array}\!\!\right.
ELU(x)={x,α×(ex−1),ifx>0otherwise
ELU对于大的、可微分的、负的输入是饱和的,这使得它们比Leaky ReLU和Parametric ReLU对噪声更稳健。
S
E
L
U
(
x
)
=
λ
×
{
x
,
α
×
(
e
x
−
1
)
,
x
≤
0
x
>
0
\mathrm{SELU}(x)=\lambda\times\left\{{x,\atop\alpha\times(e^{x}-1)\,,}\,{\overset{x\gt 0}{x\leq0}}\right.
SELU(x)=λ×{α×(ex−1),x,x≤0x>0

(注意:在x>0的区域,蓝色和红色的颜色是重叠的。)
缩放ELU(SELU)使用超参数进行缩放,这样它们就不会对巨大的正向输入产生饱和。

上文总结了ELU的变体;在所有ELU中,都考虑了大数值的饱和和应对计算成本的问题。
学习/适应性激活函数
上述的许多激活是不适应的。
o
p
e
r
a
t
o
r
n
a
m
e
A
P
L
(
x
)
=
max
(
0
,
x
)
+
∑
s
=
1
S
a
s
×
max
(
0
,
b
s
−
x
)
o p e r a t o r n a m e A P L(x)=\operatorname*{max}(0,x)+\sum_{s=1}^{S}a_{s}\times\operatorname*{max}\left(0,b_{s}-x\right)
operatornameAPL(x)=max(0,x)+s=1∑Sas×max(0,bs−x)
自适应分片线性(ALP)是一个铰链形(铰链,线图)激活函数,其中a和b是可学习的参数和S是代表铰链数量的超参数,即每个神经元有不同的a和b值,意味着每个神经元有自己的激活函数S是一个超参数,代表铰链的数量。
Swish是由Ramachandran等人提出的,并通过自动搜索找到。
o
p
e
r
a
t
o
r
n
a
m
e
S
w
i
s
h
(
x
)
=
x
×
σ
(
b
e
t
a
×
x
)
o p e r a t o r n a m e{S w i s h}(x)=x\times\sigma(b e t a\times x)
operatornameSwish(x)=x×σ(beta×x)
sigma是一个sigmoidal函数;Swish被做成类似ReLU的形式。

后来Swish被扩展到ESwish。
o
p
e
r
a
t
o
r
n
a
m
e
E
S
w
i
s
h
(
x
)
=
b
e
t
a
×
x
×
σ
(
x
)
o p e r a t o r n a m e E S w i s h(x)=b e t a\times x\times\sigma(x)
operatornameESwish(x)=beta×x×σ(x)

(注意:/beta=1.0与Swish和ESwish相匹配,所以/beta的值分别是不相连的。它们看起来仍然非常相似)
学习和适应性激活函数的定义是有一个基础激活函数,并向其添加可学习变量。例如,上述使用参数ReLU和参数ELU的自适应激活函数有 σ ( w × x ) × P R e L U ( x ) + ( 1 − σ ( w × x ) ) × \sigma(w\times x)\times\mathrm{PReLU}({\bf x})+(1-\sigma(w\times x))\times σ(w×x)×PReLU(x)+(1−σ(w×x))×有些定义为PELU(x)(σ是一个S型函数,其中w是一个可学习的变量)。
另外,每个神经元可以利用不同的激活函数。这并不意味着每个神经元由于可学习变量的不同值而使用不同的激活函数,而是字面上的不同激活函数。在一些研究中,每个神经元在ReLU和Tanh之间进行选择,并自己学习选择。
不使用可学习的超参数的非参数学习自动调节系统(non-parametrically learning AFs)也有报道,其中激活函数本身是一个非常浅的神经网络,而不是如上所述的可以写成单一公式的激活函数。这被称为超激活功能(hyperactivations),网络被称为超网络。
学习和自适应激活函数是最近的一个趋势。人们正在研究它们以应对更复杂和非线性的数据,但计算成本自然也在增加。下表总结了学习和适应性激活函数。

其他激活函数
A. Softplus激活函数
Softplus函数是在2001年提出的,在统计学中经常使用。
o p e r a t o r m e s o f t p l u s ( x ) = log ( e x + 1 ) o p e r a t o r m e s o f t p l u s(x)=\log\left(e^{x}+1\right) operatormesoftplus(x)=log(ex+1)
随后,深度学习的大行其道导致了Softmax函数的频繁使用,因为它们可以在分类任务中为每个类别输出概率值,所以具有很大的吸引力。
由于Softplus是平滑和可微分的,它类似于ReLU,也就是Softplus线性单元(SLU)。
S L U ( x ) = { α × x , x > 0 β × log ( e x + 1 ) − γ , x ≤ 0 \mathrm{SLU}(x)=\left\{\begin{array}{l l}{{\alpha\times x,}}&{{x\gt 0}}\\ {{\beta\times\log\left(e^{x}+1\right)-\gamma,}}&{{x\leq0}}\end{array}\right. SLU(x)={α×x,β×log(ex+1)−γ,x>0x≤0
alpha,β,γ是可训练的参数。
被称为Mish的激活函数是一个非单调的激活函数,同样使用Softplus。
T
a
n
h
(
x
)
=
e
x
−
e
−
x
e
x
+
e
−
x
\mathrm{Tanh}(x)={\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}}
Tanh(x)=ex+e−xex−e−x
M
i
s
h
(
x
)
=
x
×
T
a
n
h
(
S
o
f
t
p
l
u
s
(
x
)
)
\mathrm{Mish}(x)=x\times\mathrm{Tanh}(\mathrm{Softplus}({\bf x}))
Mish(x)=x×Tanh(Softplus(x))
Mish是平滑的和非单调的。它最近被用于YOLOv4中。然而,它在计算上很复杂,而且有计算成本高的缺点。

B. 随机激活函数
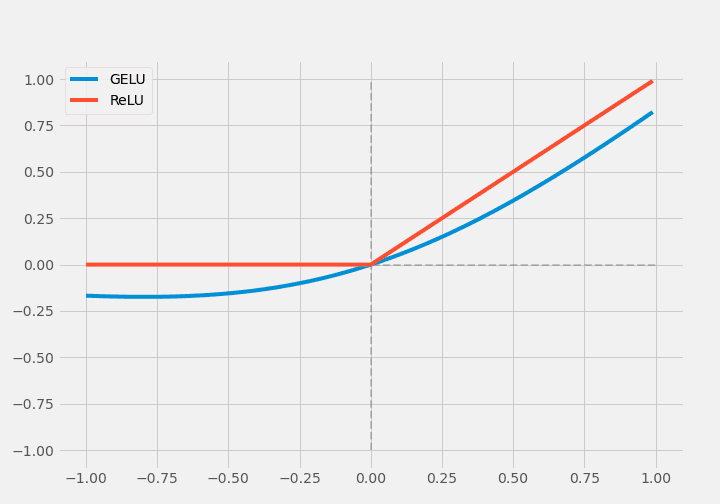
随机激活函数由于其麻烦而没有得到很好的研究;RReLU、EReLU、RTReLU和GELU是这一类中为数不多的激活函数;GELU(高斯误差线性单元)通过随机正则化考虑到了非线性问题。GELU(高斯误差线性单元)通过随机正则化考虑到了非线性问题。
o p e r a t o r n a m e G E L U ( x ) = x P ( X / l e q x ) = x P h i ( x ) o p e r a t o r n a m e{G E L}U(x)=x P(X/l e q x)=x P h i(x) operatornameGELU(x)=xP(X/leqx)=xPhi(x)
Φ被定义为
P
h
i
(
x
)
×
I
x
+
(
1
−
Φ
(
x
)
)
×
0
x
=
x
Φ
(
x
)
P h i(x)\times I x+(1-\Phi(x))\times0x=x\Phi(x)
Phi(x)×Ix+(1−Φ(x))×0x=xΦ(x),这被称为随机正则化。
C. 多项式激活函数
平滑自适应激活函数(SAAF)被开发为一个片状多项式激活函数,结合了与ReLU的线性部分对称的两个功率函数。
SAFF ( x ) = ∑ j = 0 c − 1 v j ′ m a t h r m p j ( x ) + ∑ k = 1 n w k ′ m a t h r m b k c ( x ) \operatorname{SAFF}(x)=\sum_{j=0}^{c-1}v_{j}{}^{\prime}m a t h r m p^{j}(x)+\sum_{k=1}^{n}w_{k}{}^{\prime}m a t h r m\,b_{k}^{c}(x) SAFF(x)=j=0∑c−1vj′mathrmpj(x)+k=1∑nwk′mathrmbkc(x)
ReLU也被扩展为整流动力单元(RePU), y = X S y=X^S y=XS在x>0部分(S是一个超参数)。RePU在x=0附近比ReLU更平滑。然而,易受梯度消失、无界和不对称的影响也是RePU的缺点。

近年来,利用Padé近似方法开发了Padé激活单元(PAU)。
o p e r a t o r m e P A U ( x ) = P ( x ) / Q ( x ) o p e r a t o r m e P A U(x)=P(x)/Q(x) operatormePAU(x)=P(x)/Q(x)
PAU的定义如上,其中P(x)和Q(x)分别为度数为m和n的多项式,基本上是手工设计的。
原始出版物对它的定义如上。
每个激活函数的性能比较。

上表列出了已经报道过的已经实现SOTA的激活函数。迄今为止,所描述的那些人中有Padé激活单元(MNIST on VGG8)和Swish(CIFAR10和CIFAR100 on MobileNet and ResNet)。数据集有图像、时间序列、文本等,但除了Swish之外,没有相同的激活函数在不同的数据集上实现SOTA。
在CNN上进行的实验。
这些模型是在实践中实施和比较的,而不是在纸上。该数据集是CIFAR10。

虽然数据集是通用的,但可以看出,随着模型的变化,适当的激活函数也在变化。

以上是将数据集改为CIFAR100的结果:对于MobileNet、VGG16和GoogleNet,表现最好的激活函数与CIFAR10相同,但对于ResNet50、SENet18和DenseNet121,结果有所改变(尽管在CIFAR10中表现最好的激活函数仍然表现良好)。

图中显示了每个模型的损失。激活函数是通过颜色来区分的。在图表的图例中,似乎如果激活函数低于ReLU,那么随着时间的推移,损失可以接近于零。因此,让我们比较一下100个历时所需的时间。
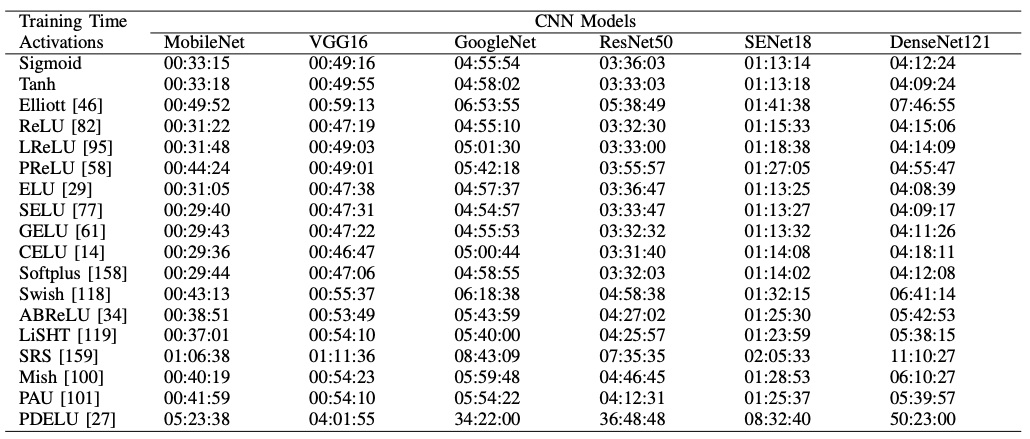
PDELU是唯一一个花了非常长的时间的人。
P D E L U ( x ) = { x , x > 0 α × ( [ 1 + ( 1 − t ) × x ] 1 1 − t − 1 ) , x ≤ 0 \mathrm{PDELU}(x)=\left\{{\begin{array}{l l}{x,}&{x\gt 0}\\ {\alpha\times\left(\left[1+(1-t)\times x\right]\frac{1}{1-t}-1\right),}&{x\leq0}\end{array}}\right. PDELU(x)={x,α×([1+(1−t)×x]1−t1−1),x>0x≤0
注:对于PDELU来说,原始出版物不是公开的,而且变量t的含义也未被证实。
结论
在深度学习中,选择合适的激活函数对于构建有效的神经网络模型至关重要。通过广泛的研究和实验,可以得出一些关于激活函数选择的结论和建议:
-
非零均值和梯度消失问题的进展:
对于logistic-sigmoidal和双曲切数(tanh)系列的激活函数,虽然已经取得了一些进展,例如通过引入非零均值来缓解梯度消失问题,但这些改进往往会增加计算成本。因此,在实际应用中需要权衡性能提升与计算成本之间的关系。 -
ReLU系列的优势:
ReLU(Rectified Linear Unit)及其变体(如Leaky ReLU和Parametric ReLU)因其简单性和效率而广受欢迎。ReLU在大多数情况下表现良好,尤其是在处理负输入时避免了梯度消失问题。因此,ReLU及其变体通常是研究人员的首选。 -
指数系列的局限性:
指数系列的激活函数主要关注负输入的处理。然而,它们在实际应用中的表现并不总是令人满意,可能存在不平滑的问题,这可能会影响模型的训练和泛化能力。 -
学习和适应系列的挑战:
虽然学习和适应系列的激活函数是一个新兴趋势,但在设置基础函数和参数数量方面存在挑战。这些激活函数需要更多的研究和实验来确定它们在不同场景下的有效性。
- 为了减少学习时间,可以选择输出平均值为零的激活函数,并确保它能够有效利用正负输入。
- 选择与数据复杂性相匹配的模型至关重要。激活函数是连接数据复杂性和模型表达能力的关键,如果两者不匹配,可能会导致过拟合或欠拟合。
- 对于卷积神经网络(CNN),应避免使用logistic-sigmoidal hyperbolic tangent系列的激活函数,而它们在循环神经网络(RNN)中可能更有用。
- 对于VGG16和GoogleNet等模型,可以考虑使用ReLU、Mish(Mixture of Softmax and Hyperbolic Tangent)和PDELU(Parametric Dual Exponential Linear Unit)等激活函数。
- 在具有残差连接的模型中,可以使用ReLU、LReLU(Leaky ReLU)、ELU(Exponential Linear Unit)、GELU(Gaussian Error Linear Unit)、CELU(Cubic Exponential Linear Unit)和PDELU等激活函数。
- 参数化激活函数通常能够更快地与数据拟合,特别是PAU(Parametric Adaptive Unit)、PReLU和PDELU。
- PDELU和SRS(Sigmoid ReLU)可能需要更长的学习时间。
- 当训练时间有限时,ReLU、SELU(Scale Exponential Linear Unit)、GELU和Softplus可能无法达到最佳性能。
- 指数系列的激活函数更有可能有效地利用负输入。
- 对于自然语言处理任务,Tanh、SELU可能是不错的选择;而PReLU、LiSHT(Leaky Sigmoid Hyperbolic Tangent)、SRS和PAU也表现良好。
- 对于语音识别任务,PReLU、GELU、Swish、Mish和PAU被认为表现良好。

![[2021最新]Java时间戳和日期时间互转换](https://img-blog.csdnimg.cn/20210420110509853.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQ0NDkxNzA5,size_16,color_FFFFFF,t_70)