文章目录
- Part.I Introduction
- Chap.I newmat 简介
- Part.II 安装与编译
- Chap.I 直接使用源码
- Chap.II 基于 CMake 使用源码
- Chap.III 编译成库
- Part.III 关于矩阵的构造与运算
- Chap.I 矩阵的构造与初始化
- Chap.II 矩阵的运算
- Chap.III 矩阵维数和类型的更改
- Chap.IV 矩阵最值统计
- Reference
Part.I Introduction
Newmat 是一个优秀的矩阵运算库,它可以用来求解线性方程组、求解特征值和最小二乘等。虽然它不像 Eigen 那样大名鼎鼎,但是在一些比较古老的软件中经常会看到它的身影,本文为笔者使用它的过程中所做的一些笔记,可能会对初步接触到它的朋友有些许帮助。

Chap.I newmat 简介
Newmat 可以用来做什么?它可以用来求解线性方程组、求解特征值和最小二乘等,其支持的矩阵类型有
| 英文 | 中文 |
|---|---|
| Matrix | 矩形矩阵 |
| UpperTriangularMatrix | 上三角矩阵 |
| LowerTriangularMatrix | 下三角矩阵 |
| DiagonalMatrix | 对角矩阵 |
| SymmetricMatrix | 对称矩阵 |
| BandMatrix | 带矩阵 |
| UpperBandMatrix | 上三角带矩阵 |
| LowerBandMatrix | 下三角带矩阵 |
| SymmetricBandMatrix | 对称带矩阵 |
| RowVector | 行矩阵 |
| ColumnVector | 列矩阵 |
| IdentityMatrix | 具有相同值的对角矩阵 |
该库包括操作*,+,-,*=,+=,-=,Kronecker 积,Schur 积,串联,逆,转置,类型之间的转换,子矩阵,行列式,Cholesky 分解,QR 三角化,奇异值分解,对称矩阵的特征值,排序,快速傅里叶和三角等。它适用于范围为10 × 10到您的机器将在单个数组中容纳的最大尺寸的矩阵。该包适用于非常小的矩阵,但变得相当低效。
Part.II 安装与编译
首先从官网下载源码
Chap.I 直接使用源码
下载解压好之后会看到文件夹中有个 nm11.htm,这个文件就是它的说明文档,双击打开,找到它的文件内容说明,我们需要的最核心的代码文件主要有下面的一些:

我们只需要上面的这 36(11*.h+25*.cpp)个文件即可。首先将这36个文件提出来放到一个文件夹(比如nm_src)中。
1、新建一个 VS C++ 空项目nm_test,将nm_src拷贝到项目所在文件夹
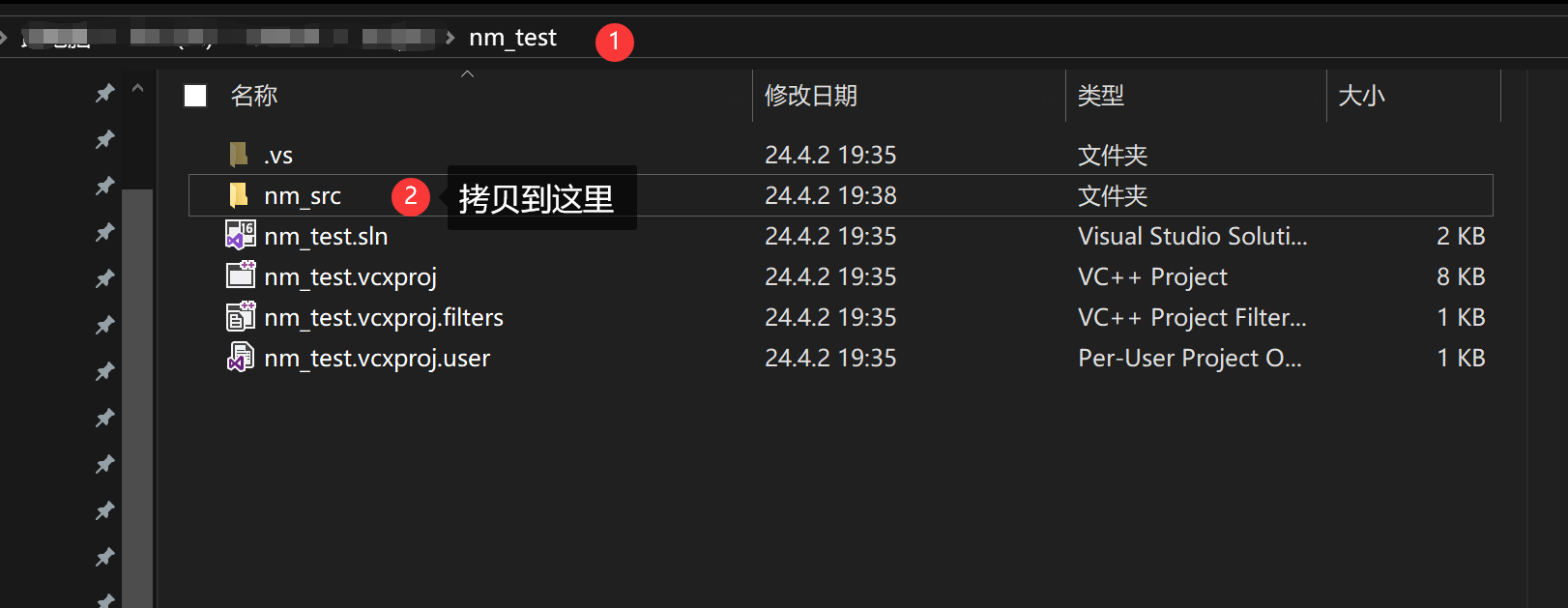
2、在 VS Studio 中选中 nm_test 项目,右键→添加→现有项→快捷键 Ctrl + A 全选→添加
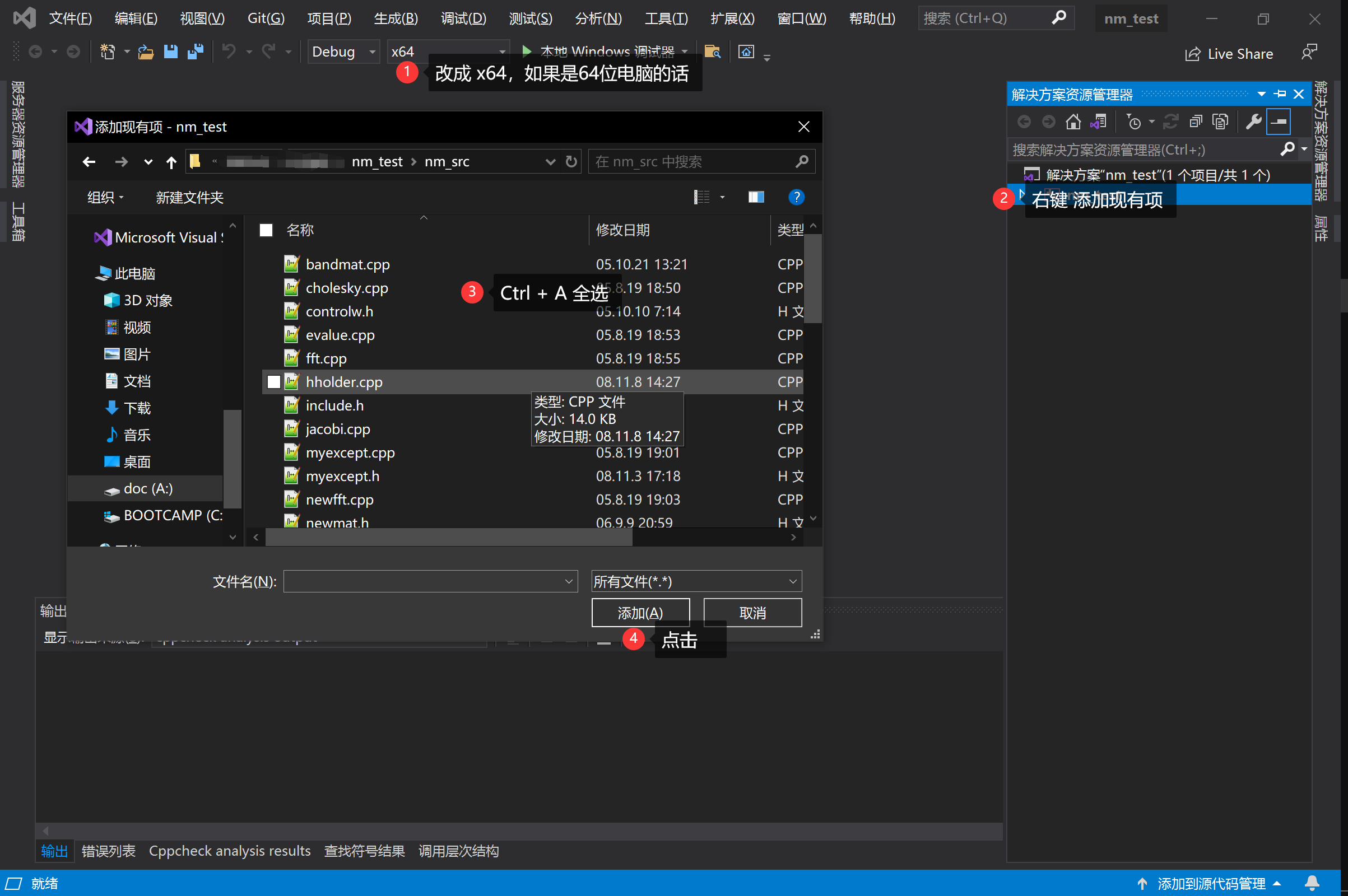
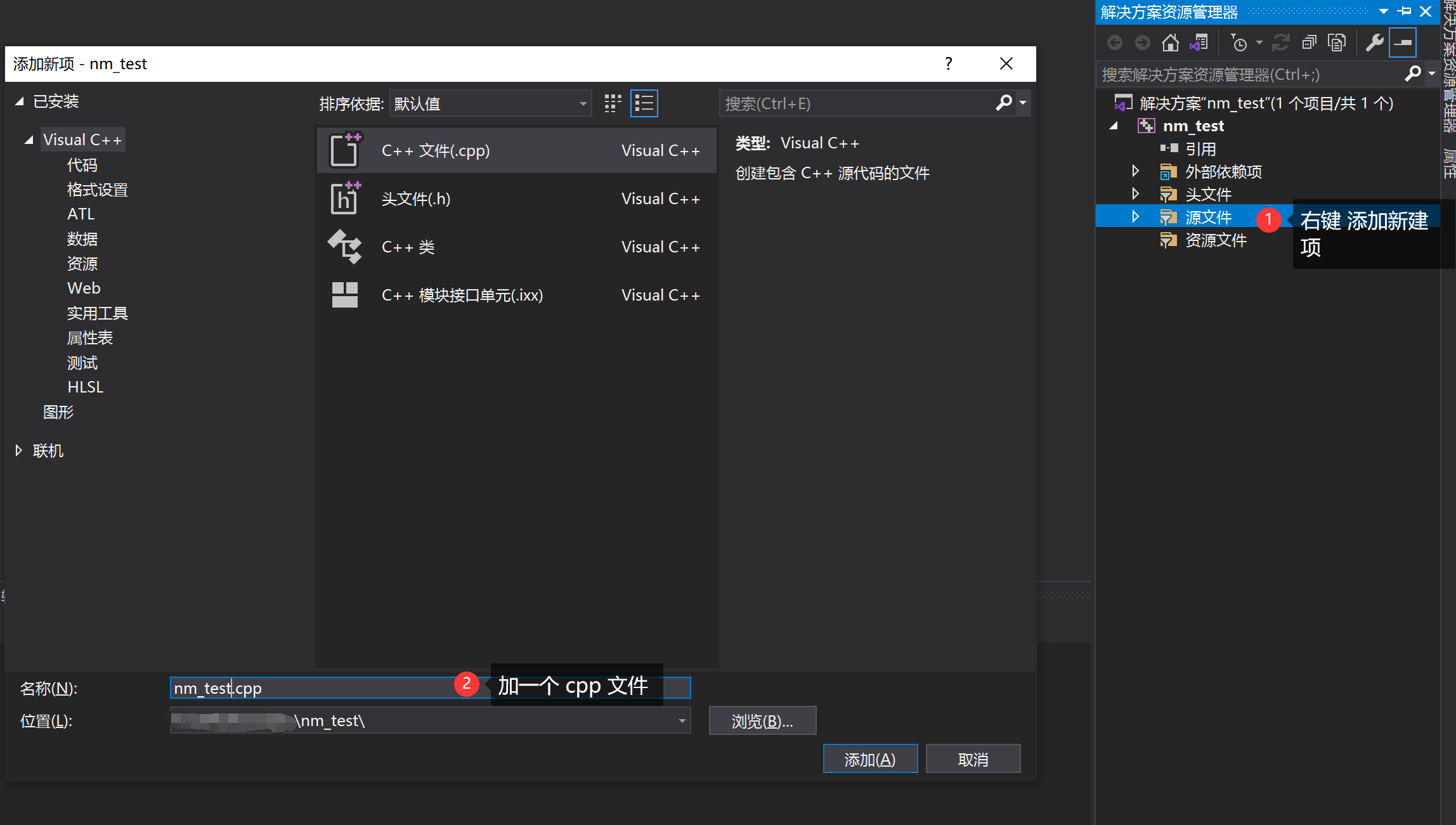
3、选中源文件→右键添加→新建项→加一个新的 cpp 文件nm_test.cpp
4、将下面的代码贴到 nm_test.cpp 文件中,
/// \ingroup newmat
///@{
/// \file nm_ex1.cpp
/// Very simple example 1.
/// Invert a 4 x 4 matrix then check the result
#define WANT_STREAM // include iostream and iomanipulators
#include "nm_src/newmatap.h" // newmat advanced functions
// should not be required for this example
// included because it seems to help MS VC6
// when you have namespace turned on
#include "nm_src/newmatio.h" // newmat headers including output functions
#ifdef use_namespace
using namespace RBD_LIBRARIES;
#endif
int my_main() // called by main()
{
Tracer tr("my_main "); // for tracking exceptions
// declare a matrix
Matrix X(4, 4);
// load values row by row
X.row(1) << 3.7 << -2.1 << 7.4 << -1.0;
X.row(2) << 4.1 << 0.0 << 3.9 << 4.0;
X.row(3) << -2.5 << 1.9 << -0.4 << 7.3;
X.row(4) << 1.5 << 9.8 << -2.1 << 1.1;
// print the matrix
cout << "Matrix X" << endl;
cout << setw(15) << setprecision(8) << X << endl;
// calculate its inverse and print it
Matrix Y = X.i();
cout << "Inverse of X" << endl;
cout << setw(15) << setprecision(8) << Y << endl;
// multiply X by its inverse and print the result (should be near identity)
cout << "X * inverse of X" << endl;
cout << setw(15) << setprecision(8) << (X * Y) << endl;
return 0;
}
// call my_main() - use this to catch exceptions
// use macros for exception names for compatibility with simulated exceptions
int main()
{
Try{ return my_main(); }
Catch(BaseException) { cout << BaseException::what() << "\n"; }
CatchAll{ cout << "\nProgram fails - exception generated\n\n"; }
return 0;
}
///@}
5、先别慌运行,选中项目右键→属性→C/C++→预处理器→预处理器定义→下拉三角编辑→加入_CRT_SECURE_NO_WARNINGS
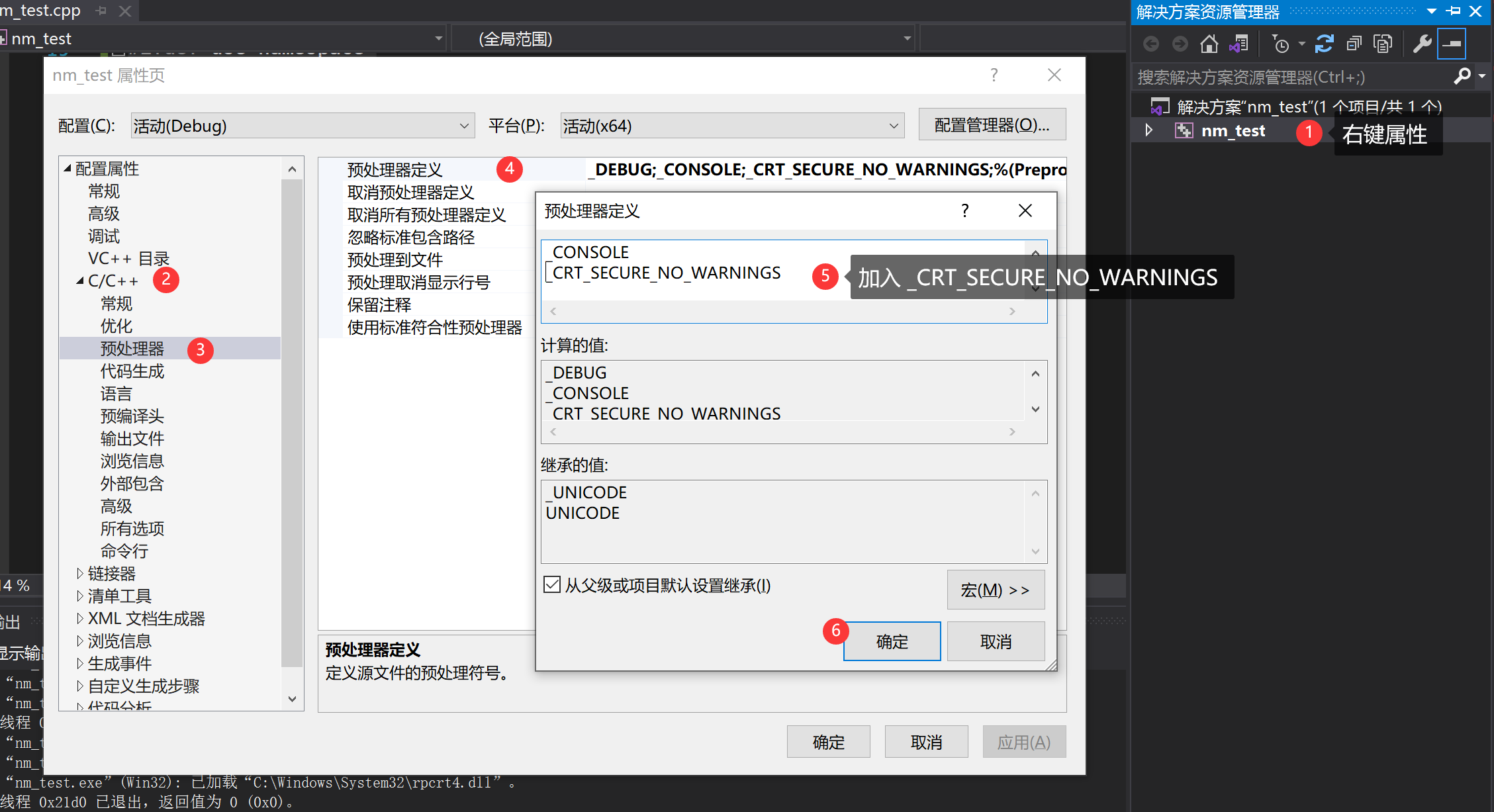
6、快捷键 F5 运行得到结果:
Chap.II 基于 CMake 使用源码
和上面比较类似,只不过需要注意如下几点:
- 要有
#define Libxxx_LIBRARY_EXPORT __declspec(dllexport),并且修改newmat的头文件,在每个类和类外函数前加修饰Libxxx_LIBRARY_EXPORT,否则会报错LNK1104 无法打开文件“..\Lib\RelWithDebInfo\Libxxxrd.lib” CMakeLists.txt文件中要加入add_definitions(-D _CRT_SECURE_NO_WARNINGS),这样就不用进行上面第 5 步预处理器定义编辑操作了
Chap.III 编译成库
编译成库,有两种,一种是动态链接库 dll,另一种是静态库 lib,lib是编译时需要的,dll是运行时需要的。
这部分另开了一篇博文介绍,请戳我跳转
Part.III 关于矩阵的构造与运算
这部分是笔者在使用 newmat 矩阵库的时候所作的笔记。首先需要注意下面的一些信息:
- 矩阵行列索引都是从 1 开始的
- 不能直接把一个数组赋值给对称矩阵
Chap.I 矩阵的构造与初始化
矩阵的构造
Matrix A(m,n); // m*n 的矩阵
RowVector RV(n); // 1*n 的行矩阵
ColumnVector CV(n); // n*1 的列矩阵
DiagonalMatrix D(n); // n 维的对角阵
SymmetricMatrix S(n); // n 维的对称阵
UpperTriangularMatrix UT(n); // n 维的上三角矩阵
LowerTriangularMatrix LT(n); // n 维的下三角矩阵
矩阵的初始化有多种方式,下面一一列举
1、所有元素均初始化为 0
Matrix A(m, n);
A = 0.0;
2、通过数组初始化
Matrix A(3,2);
Real a[] = { 11,12,21,22,31,33 };
A << a;
3、给矩阵中某个元素赋值
A(i,j) << 2;
4、给矩阵中一行的元素赋值
Matrix A(3,2);
A.Row(1) << 11 << 12;
5、拷贝赋值
A.Inject(B); // 将 B 拷贝给 A
Chap.II 矩阵的运算
一元运算:求取矩阵的『特征』(秩、迹、行列式、范数等)
X = -A; // 符号取反
X = A.t(); // 转置
X = A.i(); // 求逆
X = A.Reverse(); // 顺序翻转 (不适用于带状矩阵)
Real t = A.Trace(); // 迹
Real d = A.Determinant(); // 行列式
Real r = A.AsScalar(); // value of 1x1 matrix
Real ssq = A.SumSquare(); // 所有元素的平方和
Real sav = A.SumAbsoluteValue(); // 所有元素绝对值之和
Real s = A.Sum(); // 所有元素之和
Real norm = A.Norm1(); // 列范数,列向量元素绝对值之和的最大值
Real norm = A.NormInfinity(); // 无穷范数,行向量元素绝对值之和的最大值
Real norm = A.NormFrobenius(); // F-范数,square root of sum of squares of the elements
LogAndSign ld = A.LogDeterminant(); // log(行列式)
bool z = A.IsZero(); // 判断矩阵是否所有元素都为 0
bool s = A.IsSingular(); // A is a CroutMatrix or BandLUMatrix
二元运算:两个矩阵间作运算
X = A + B; // 加
X = A - B; // 减
X = A * B; // 乘
X = A.i() * B; // A^{-1}*B
X = A | B; // 把 A 和 B 水平连接起来(AB行数需相等)
X = A & B; // 把 A 和 B 竖直连接起来(AB列数需相等)
X = SP(A, B); // A 和 B 的 schur 积(AB行列数需相等,对应元素相乘,得到一个新的矩阵)
X = KP(A, B); // A 和 B 的 Kronecker 积(将矩阵视作向量)
Real s = DotProduct(A, B); // A 和 B 的点积(将矩阵视作向量)
bool b = A == B; // A B 是否相等
bool b = A != B; // ! (A == B)
A += B; // A = A + B;
A -= B; // A = A - B;
A *= B; // A = A * B;
A |= B; // A = A | B;
A &= B; // A = A & B;
<, >, <=, >= // 保持和 STL 的兼容性
Chap.III 矩阵维数和类型的更改
A.ReSize(nrows,ncols); // for type Matrix or nricMatrix
A.ReSize(n); // for all other types, except Band
A.ReSize(n,lower,upper); // for BandMatrix
A.ReSize(n,lower); // for LowerBandMatrix
A.ReSize(n,upper); // for UpperBandMatrix
A.ReSize(n,lower); // for SymmetricBandMatrix
A.ReSize(B); // set dims to those of B
A.AsRow()
A.AsColumn()
A.AsDiagonal()
A.AsMatrix(nrows,ncols)
A.AsScalar()
A.Release() // 结构体矩阵,释放内存
m_ReleaseAndDelete() // 指针矩阵,释放内存
Chap.IV 矩阵最值统计
使用前最好先测一下,笔者暂时没有测过。
Real mv = A.MaximumAbsoluteValue(); // 返回 A 所有元素最大的绝对值
Real mv = A.MinimumAbsoluteValue(); // 返回 A 所有元素最小的绝对值
Real mv = A.Maximum(); // 返回 A 中最大的元素
Real mv = A.Minimum(); // 返回 A 中最小的元素
Real mv = A.MaximumAbsoluteValue1(i); // maximum of absolute values
Real mv = A.MinimumAbsoluteValue1(i); // minimum of absolute values
Real mv = A.Maximum1(i); // maximum value
Real mv = A.Minimum1(i); // minimum value
Real mv = A.MaximumAbsoluteValue2(i,j);// maximum of absolute values
Real mv = A.MinimumAbsoluteValue2(i,j);// minimum of absolute values
Real mv = A.Maximum2(i,j); // maximum value
Real mv = A.Minimum2(i,j); // minimum value
Reference
- newmat 的简单使用
- newmat 官方文档
- C++ newmat 指北