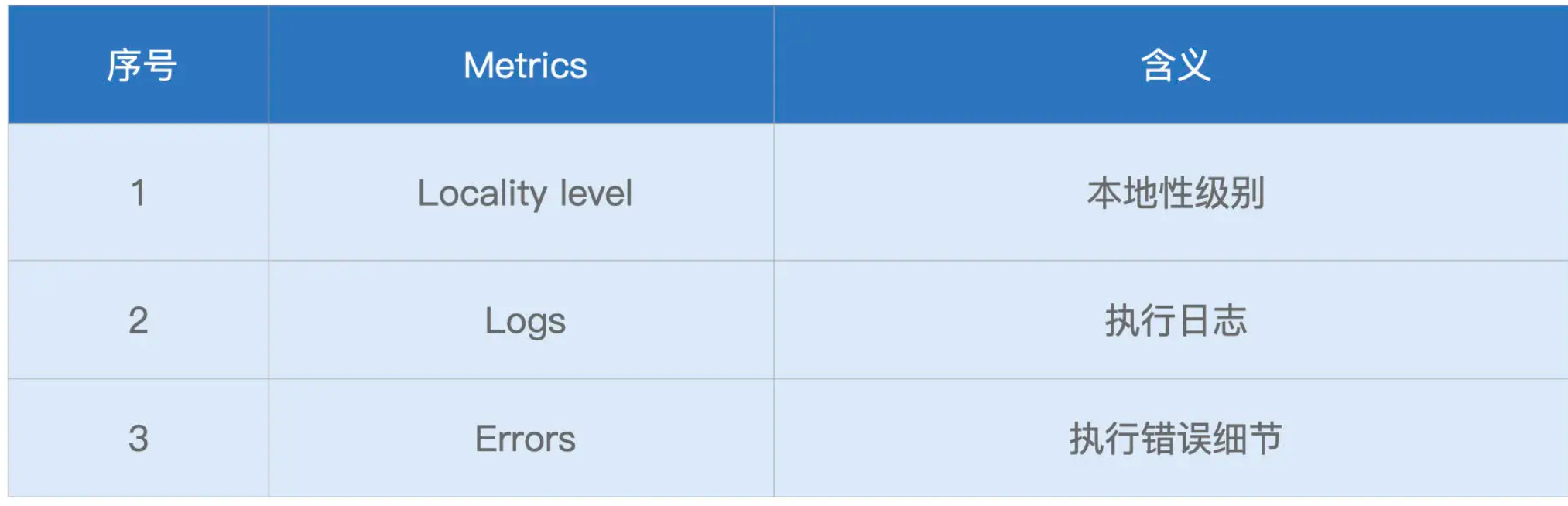
在git中，将一个分支的更改集成到另一个分支有两种主要方式：合并（merge）和变基（rebase）。在本节中，将学习什么是变基，如何执行变基操作，为什么它是一个非常强大的工具，以及在哪些情况下不希望使用它。

基本变基

如果回到基本合并的一个早期示例，会发现工作分叉了，并在两个不同的分支上进行了提交。

正如我们已经介绍过的那样，最简单的集成分支的方法是使用合并（merge）命令。它在两个最新的分支快照（C3和C4）与两者的最近公共祖先（C2）之间执行三方合并，创建一个新的快照（和提交）。

然而，还有另一种方法：可以获取在C4引入的更改补丁，并将其重新应用在C3之上。在git中，这被称为变基（rebase）。使用rebase命令，可以获取在一个分支上提交的所有更改，并在不同的分支上重放它们。

对于这个示例，将检出experiment分支，然后将其变基到master分支上，如下所示：

$ git checkout experiment

$ git rebase master

First, rewinding head to replay your work on top of it...

Applying: added staged command

这个操作通过前往两个分支的共同祖先（当前所在的分支和要变基到的分支），获取当前分支中每个提交引入的差异，将这些差异保存到临时文件中，将当前分支重置为与要变基到的分支相同的提交，最后依次应用每个更改。

在这一点上，可以返回到master分支并执行快进合并。

$ git checkout master

$ git merge experiment

现在，C4'指向的快照与合并示例中C5所指向的快照完全相同。集成的最终产品没有任何区别，但变基使历史记录更清晰。如果检查变基分支的日志，它看起来像是一个线性的历史记录：似乎所有的工作都是按顺序完成的，即使最初是并行完成的。

通常，会这样做来确保提交在远程分支上能够干净地应用 - 也许是试图贡献但不维护的项目中。在这种情况下，会在一个分支上进行工作，然后在准备好向主项目提交补丁时，将的工作变基到origin/master分支上。这样，维护者就不需要进行任何集成工作 - 只需要一个快进合并或一个干净的应用。

请注意，无论最终得到的最终提交是变基的最后一个提交还是合并后的最终合并提交，指向的快照都是相同的 - 只有历史记录是不同的。变基将一系列工作中的更改按照它们被引入的顺序重播到另一条线上，而合并则将端点合并在一起。

更有趣的变基

还可以将变基回放到除了变基目标分支之外的其他地方。例如，考虑一个像这样的历史：从另一个主题分支分出的一个主题分支。例如，从一个主题分支（server）分出一个分支，为项目添加了一些服务器端功能，并提交了一个提交。然后，从该分支分出一个分支（client）来进行客户端更改，并进行了几次提交。最后，回到了服务器分支并进行了几次提交。

假设决定要将客户端的更改合并到主线以进行发布，但想等到服务器端的更改经过进一步测试。可以使用git rebase的--onto选项，将客户端上不在服务器上的更改（C8和C9）重播到主分支上：

$ git rebase --onto master server client

这基本上是在说：“获取客户端分支，找出自从它与服务器分支分叉以来的补丁，并在客户端分支上重播这些补丁，就好像它直接基于主分支。” 这有点复杂，但结果非常酷。

现在可以将主分支快进（参见主分支快进以包含客户端分支的更改）:

$ git checkout master

$ git merge client

假设决定同时合并服务器分支。可以在无需首先检出它的情况下，通过运行git rebase <基础分支> <主题分支> 将服务器分支变基到主分支上 - 这会检出主题分支（在本例中是服务器分支）并将其重播到基础分支（主分支）上:

$ git rebase master server

这会将服务器工作重播主分支工作之上

然后，可以快进基础分支（主分支）:

$ git checkout master

$ git merge server

可以删除客户端和服务器分支，因为所有工作都已集成，不再需要它们，使得整个过程的历史记录看起来像是最终提交历史:

$ git branch -d client

$ git branch -d server

变基的危险

但是变基的喜悦并不是没有缺点的，可以用一句话概括：

不要变基已经存在于存储库之外的提交，可能有人基于这些提交进行工作。

如果遵循这个准则，那么一切都会很好。如果不遵循，人们会讨厌women ，会受到朋友和家人的蔑视。

当重新定位工作时，会放弃现有的提交并创建新的提交，这些提交类似但有所不同。如果推送提交到某个地方，其他人将其拉取下来并基于其进行工作，然后用git rebase重写这些提交并再次推送它们上去，那么合作者将不得不重新合并他们的工作，当试图将他们的工作拉回我们的工作时，事情会变得混乱。

让我们看一个例子，说明如何对已经公开的工作进行变基可能会导致问题。假设从一个中央服务器克隆，然后对其进行一些工作。提交历史如下所示：

现在，其他人做了更多的工作，其中包括一个合并，并将该工作推送到中央服务器。 获取了它并将新的远程分支合并到您的工作中，使历史看起来像这样：

接下来，推送合并工作的人决定返回并重新定位他们的工作； 他们执行git push --force以覆盖服务器上的历史记录。 然后，从该服务器获取，将新的提交拉取下来。

现在你们两个都陷入了困境。 如果你执行git pull，将创建一个合并提交，其中包含两行历史记录，你的存储库将如下所示：

如果在我们历史记录呈现此样式时运行git log，将看到两个提交具有相同的作者、日期和消息，这将令人困惑。此外，如果将此历史记录推送回服务器，将重新引入所有这些已重新定位的提交到中央服务器，这可能会进一步使人困惑。可以相当肯定地假设另一个开发人员不希望C4和C6出现在历史记录中；这就是他们首先进行重新定位的原因。

重新定位时进行重新定位

如果发现自己处于这种情况，Git 还有一些进一步的魔法可能会帮助您解决问题。如果团队中的某人强制推送了覆盖我们基于其进行工作的更改，我们挑战就是找出哪些是我们的，哪些是他们重新编写的。

事实证明，除了提交的 SHA-1 校验和之外，git 还计算了一个仅基于引入的补丁的校验和。这被称为“补丁 ID”。

如果拉取了被重写的工作，并将其重新定位到我们的合作伙伴的新提交之上，git 通常可以成功地确定哪些是我们独有的，并将它们应用到新分支的顶部。

例如，在先前的场景中，如果我们在当我们在有人推送重新定位的提交时，放弃了我们基于其进行工作的提交时，我们运行 git rebase teamone/master，git 将会：

确定哪些工作是我们分支独有的（C2、C3、C4、C6、C7）

确定哪些不是合并提交（C2、C3、C4）

确定哪些没有被重写到目标分支中（仅 C2 和 C3，因为 C4 与 C4' 是相同的补丁）

将这些提交应用到 teamone/master 的顶部

因此，我们不会像在“再次合并相同的工作以生成新的合并提交”中看到的结果那样结束，而是会得到类似“在被强制推送的重新定位工作之上重新定位”的结果。

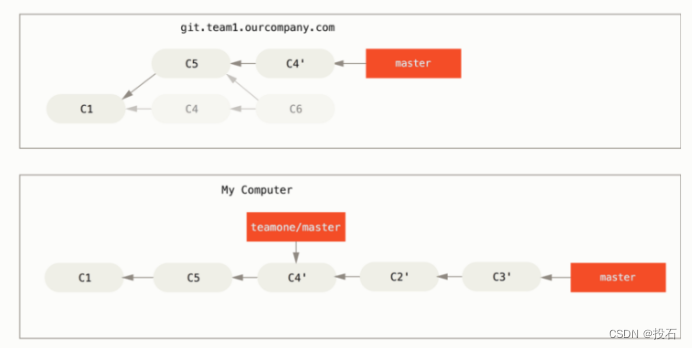
这只有在合作伙伴制作的 C4 和 C4' 几乎完全相同的补丁时才有效。否则，重新定位将无法确定它是重复的，并将添加另一个类似于 C4 的补丁（这可能会导致应用失败，因为更改已经存在）。

还可以通过运行 git pull --rebase 而不是普通的 git pull 来简化此过程。或者，在这种情况下，也可以手动执行 git fetch，然后执行 git rebase teamone/master。

如果使用 git pull 并希望将 --rebase 设置为默认值，可以使用类似 git config --global pull.rebase true 的命令来设置 pull.rebase 配置值。

如果只重新定位从未离开过计算机的提交，那么一切都会很好。如果重新定位已经推送过的提交，但没有人基于这些提交创建新的提交，那么一切也会很好。如果重新定位已经公开推送的提交，而且人们可能已经基于这些提交进行了工作，那么可能会遇到一些令人沮丧的麻烦，并且会受到队友的责备。

如果我们或合作伙伴在某个时候发现有必要这样做，请确保每个人都知道运行 git pull --rebase 来尝试使发生这种情况后的痛苦变得简单一些。

重新定位 vs. 合并

现在已经看到了重新定位和合并的实际操作，可能想知道哪个更好。在我们回答这个问题之前，让我们稍微退后一步，谈谈历史意味着什么。

对此的一种观点是，存储库的提交历史记录是实际发生的事情的记录。它是一份历史文档，本身就有价值，不应该被篡改。从这个角度来看，更改提交历史几乎是亵渎的；那么如果有一系列混乱的合并提交怎么办？这就是实际发生的事情，存储库应该为后人保留下来。

相反的观点是，提交历史记录是项目是如何制作的故事。不会发布一本书的初稿，那么为什么要展示混乱工作呢？当在项目上工作时，可能需要记录所有错误和死胡同，但是当准备向世界展示我们工作时，我们可能希望讲述如何从 A 到 B 的更连贯的故事。在这个阵营中，人们使用像重新定位和 filter-branch 这样的工具，在将其合并到主干分支之前重新编写他们的提交。他们使用重新定位和 filter-branch 这样的工具，以最适合未来读者的方式讲述故事。

现在，关于合并和重新定位哪个更好的问题：希望能看到这并不简单。git 是一个强大的工具，可以让我们对历史进行许多操作，但每个团队和每个项目都是不同的。现在我们知道这两个工作原理了，就由我们自己来决定哪个对特定情况更好。

可以两全其美：在推送本地更改之前重新定位以清理您的工作，但不要重新定位已经推送到其他地方的任何内容。