题目
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1:
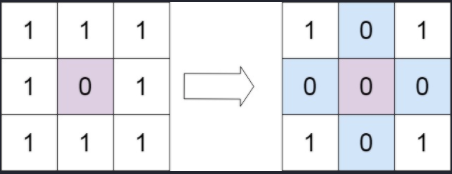
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
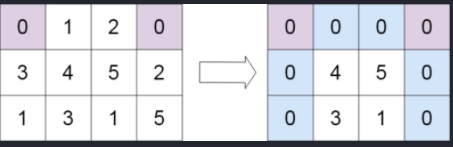
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-231 <= matrix[i][j] <= 231 - 1
题解
看到这题的时候我们第一时间肯定想申请一个跟原始matrix二维数组一模一样的数组A,遍历matrix来保存而为素组matrix中为0元素的位置。然后再遍历A将martix中对应的行和列的元素置为0。
public void setZeroes(int[][] matrix) {
boolean[] row = new boolean[matrix.length];
boolean[] col = new boolean[matrix[0].length];
for (int i = 0; i < matrix.length; i ++) {
for (int j = 0; j < matrix[0].length; j ++) {
if (matrix[i][j] == 0) {
row[i] = true;
col[j] = true;
}
}
}
for (int i = 0; i < matrix.length; i ++) {
for (int j = 0; j < matrix[0].length; j ++) {
if (row[i] || col[j]) {
matrix[i][j] = 0;
}
}
}
}

看到这种方式空间使用率会很比较高大概O(2mn),这个时候有没有更好的解决办法呢!我用List<Map<String, String>> 包装类型来放为0元素的位置应该会小一点吧? 因为我只需要存特定是0的位置,其他的不为0的位置我不需要存。说干就干,试验一下:
public void setZeroes(int[][] matrix) {
List<Map<Integer, Integer>> list = new ArrayList<>();
for (int i = 0; i < matrix.length; i ++) {
for (int j = 0; j < matrix[0].length; j ++) {
if (matrix[i][j] == 0) {
HashMap<Integer, Integer> integerHashMap = new HashMap<>();
integerHashMap.put(i, j);
list.add(integerHashMap);
}
}
}
for (Map<Integer, Integer> data : list) {
data.forEach((k, v) -> {
for (int i = 0; i < matrix.length; i++) {
matrix[i][v] = 0;
}
for (int i = 0; i < matrix[0].length; i++) {
matrix[k][i] = 0;
}
});
}
}
可以看到空间使用率确实是好了一点,但是我们效率变得非常低了,执行时间只击败了17%的用户。而且空间利用率也不是很完美,主要也是包装类型本身也需要占用一些空间。有没有更好的方案呢?我们接着往下看。
进阶:
一个直观的解决方案是使用 O(mn) 的额外空间,但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(m + n) 的额外空间,但这仍然不是最好的解决方案。
你能想出一个仅使用常量空间的解决方案吗?
public void setZeroes(int[][] matrix) {
boolean firstRowHasZero = false;
boolean firstColHasZero = false;
// 检查第一行是否有零
for (int i = 0; i < matrix[0].length; i++) {
if (matrix[0][i] == 0) {
firstRowHasZero = true;
break;
}
}
// 检查第一列是否有零
for (int i = 0; i < matrix.length; i++) {
if (matrix[i][0] == 0) {
firstColHasZero = true;
break;
}
}
// 使用第一行和第一列记录零的位置
for (int i = 1; i < matrix.length; i++) {
for (int j = 1; j < matrix[0].length; j++) {
if (matrix[i][j] == 0) {
matrix[i][0] = 0;
matrix[0][j] = 0;
}
}
}
// 根据第一行和第一列的记录,将对应的行和列置零
for (int i = 1; i < matrix.length; i++) {
for (int j = 1; j < matrix[0].length; j++) {
if (matrix[i][0] == 0 || matrix[0][j] == 0) {
matrix[i][j] = 0;
}
}
}
// 如果第一行有零,则将第一行置零
if (firstRowHasZero) {
for (int i = 0; i < matrix[0].length; i++) {
matrix[0][i] = 0;
}
}
// 如果第一列有零,则将第一列置零
if (firstColHasZero) {
for (int i = 0; i < matrix.length; i++) {
matrix[i][0] = 0;
}
}
}
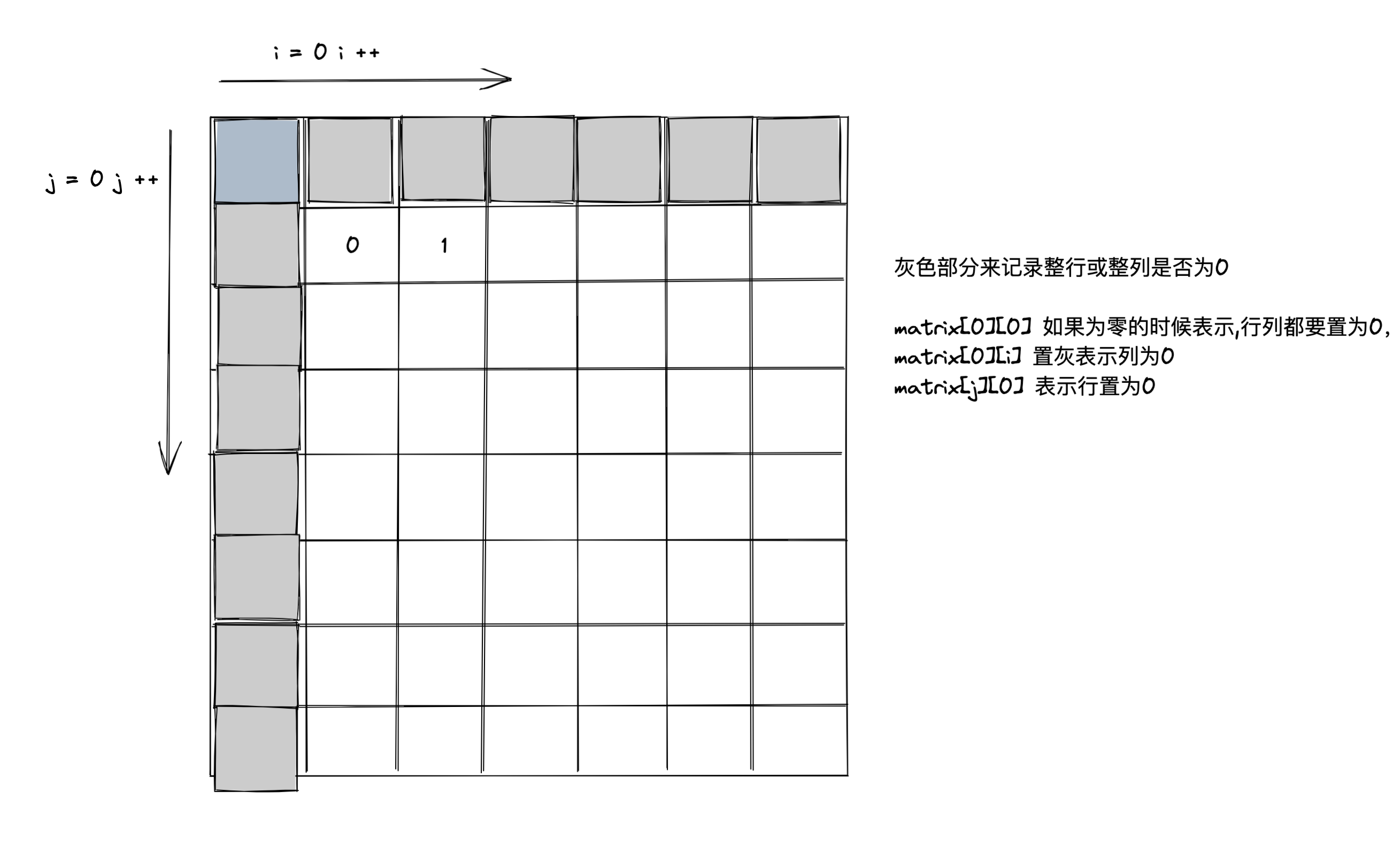
这个优化后的代码使用了两个布尔变量来记录第一行和第一列是否有零。然后,通过遍历矩阵,使用第一行和第一列来记录零的位置。最后,根据这些记录,将对应的行和列置零。最后,根据第一行和第一列的记录,将第一行和第一列本身置零(如果需要)。
通过这种方法,我们只使用了常量级的额外空间来完成操作,将空间复杂度降到了最低。
总结
上述算法是对给定二维矩阵进行优化,以降低空间复杂度的算法。该算法使用常量级的额外空间来实现。
首先,算法通过遍历矩阵,检查第一行和第一列是否存在零,并使用两个布尔变量记录下来。接下来,算法再次遍历矩阵,将零的位置记录在第一行和第一列中,即如果某个元素为零,就将对应的第一行和第一列的元素置零。
然后,算法再次遍历矩阵,根据第一行和第一列的记录,将对应的行和列置零。具体实现时,如果某个元素所在的行的第一列元素或所在的列的第一行元素为零,则将该元素置零。
最后,算法根据最开始记录的两个布尔变量,如果第一行或第一列存在零,则将整行或整列置零。
通过这种优化方法,算法只使用了常量级的额外空间来完成操作,将空间复杂度降到了最低。这种算法的时间复杂度为O(m×n),其中m是矩阵的行数,n是矩阵的列数。
总之,该算法通过巧妙地利用矩阵的第一行和第一列来记录零的位置,并根据这些记录将对应的行和列置零,从而实现了对给定矩阵的优化。这种优化方法在空间复杂度方面非常高效,适用于处理大规模的二维矩阵。