学生问了一个问题:

这个问题如果想讲明白,需要将基础知识复习一下。
一、定点数
1、什么是定点数?
定点数指小数点在数中位置固定不变的数。
详细解释:计算机中小数点的位置固定不变,小数点前、后的数字,分别用二进制表示,组合起来,就可以在计算机中存储起来,这种表示方式叫做定点表示法,用这种方法表示的数字叫做定点数。
「定」是指固定的意思
「点」是指小数点,小数点位置固定
即定点数
2、定点数表示数字
数字分三种情况:
纯整数: 整数100,小数点其实在最后一位,所以忽略不写
纯小数: 0.123,小数点固定在最高位
整数+小数:3.14、21.34,345.67小数点在指定某个位置
以下都以 1 个字节(8 bit)表示
(1)纯整数表示
对于纯整数,小数点固定在最低位
100(十) = 01100100(二)
将十进制数100转换为二进制,可以使用除2取余法:
首先,将100除以2,商为50,余数为0。
接着,将50除以2,商为25,余数为0。
然后,将25除以2,商为12,余数为1。
继续,将12除以2,商为6,余数为0。
再次,将6除以2,商为3,余数为0。
然后,将3除以2,商为1,余数为1。
最后,将1除以2,商为0,余数为1。
现在,从最后一个余数开始,依次写下所有余数,得到的结果就是100的二进制表示。
100的二进制表示为1100100
(2)纯小数表示
纯小数,如 0.124,由于小数点固定在最高位
0.124(十)=0.00111101(二)
要将小数0.124转换为二进制,可以使用乘2取整法:
开始时,将0.124乘以2,得到0.248,这意味着第一个二进制位是0。
然后,将0.248的小数部分继续乘以2,得到0.496,所以第二位是0。
接下来,将0.496的小数部分继续乘以2,得到0.992,所以第三位是0。
然后,将0.992的小数部分继续乘以2,得到1.984,所以第四位是1。
然后,将0.984的小数部分继续乘以2,得到1.968,所以第五位是1。
然后,将0.968的小数部分继续乘以2,得到1.936,所以第六位是1。
然后,将0.936的小数部分继续乘以2,得到1.872,所以第七位是1。
最后,将0.872的小数部分继续乘以2,得到1.744,所以第八位是1。
因此,0.124的二进制表示为0.00111101。
(3)整数+小数 表示
以 1 个字节(8 bit)为例,约定前 5 位表示整数部分,后 3 位表示小数部分
2.5定点数表示:
2.5(十)=00010.100(二)
将2.5转换为二进制,分别转换整数部分和小数部分,然后将它们合并:
整数部分5位表示:2.5的整数部分是2,其二进制表示为10。由于要用5位表示,需要在前面补零,所以整数部分的二进制表示为00010。
小数部分3位表示:0.5的二进制表示为0.1。由于要用3位表示,需要将小数点后的位数补齐,所以小数部分的二进制表示为100。
因此,2.5的二进制表示为00010.100。
15.225的二进制表示为01111.001
定点数表示数字过程:
(1)在有限的 bit(位) 宽度下,先约定小数点的位置
(2)整数部分和小数部分,分别转换为二进制表示
(3)将两部分二进制组合起来,即是结果
3、问题
约定了前 5 位表示整数部分,后 3 位表示小数部分,
整数部分的二进制最大值只能是 11111,即十进制的 31
小数部分的二进制最大只能表示 0.111,即十进制的 0.875。
用定点数表示的小数,不仅数值的范围表示有限,而且其精度也很低
如果想要表示更大范围的值呢?
提出了使用**“浮点数”**的方式表示数字
二、原码、反码、补码与移码
由于计算机的硬件决定,任何存储于计算机中的数据,其本质都是以二进制码存储。
根据冯·诺依曼提出的计算机体系结构框架,一台计算机由运算器、控制器、存储器、输入和输出设备组成。
其中运算器只有加法运算器,没有减法运算器
所以计算机中的减法是通过加法实现的,减去一个数可以看作加上这个数的相反数,必须有负数,所以引入一个符号位。
符号位在内存中存放的最左边一位,如符号位为0,则说明该数为正;若为1,则说明该数为负。
原码、反码、补码的产生过程就是为了解决计算机做减法和引入符号位的问题。
1、原码
是最简单的机器数表示法,用最高位表示符号位,其他位存放该数的二进制的绝对值
5的二进制:0101
23的二进制:00010111
负数:
如:四位表示,带符号位,1010,最高位为1表示这是一个负数,其它三位010
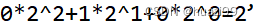
所以1010表示十进制数-2。
如图:
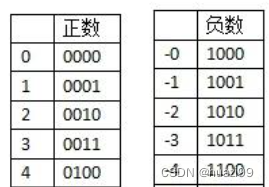
运算:
0001+0010=0011,1+2=3 正确
0000+1000=1000,+0+(-0)=-0 错误
0001+1001=1010,1+(-1)=-2 错误
正数与正数相加正确,就是一个很简单的二进制加法,而正数与负数相加,或负数与负数相加,错误,这是符号位引起的。
总结: 原码不便进行加减运算。
2、反码
一个数加上该数的相反数应该等于0
但原码是一个数加上它的相反数不等于0
0001+1001=1010,1+(-1)=-2,提出“反码”
反码: 正数的反码还是等于原码;负数的反码就是它的原码除符号位外,按位取反
如:3是正数,反码与原码相同,则可以表示为四位0011;
-3的原码是1011,符号位保持不变,低三位按位取反,所以-3的反码为1100。
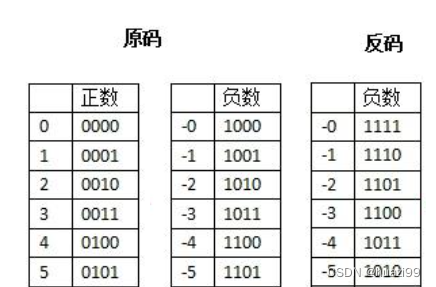
运算:
0001+1110=1111,1+(-1)=-0; 正确
1110+1100=1010,(-1)+(-3)=-5。 错误
两个负数相加的出错
3、补码
补码:正数的补码等于它的原码;负数的补码等于反码+1
1 原码 0001
2 原码 0010
0001+0010=0011 1+2=3 正确
1 原码 0001
-1原码 1001 反码1110 补码 1111
0001+1111=0000 1+(-1)=0 正确
-1原码 1001 反码1110 补码 1111
-3原码 1011 反码1100 补码 1101
1111+1101=1100 (-1)+(-3)=-4 正确
补码的出现是为了解决负数计算的问题
补码原理-- 模 同余数
自行查看相关文章
4、移码(增码或偏置码)
移码是在原码的基础上加上一个偏移量(K)的表示。对于有符号数,移码的表示范围通常在-K到K之间。移码的目的是将有符号数转换为无符号数来进行计算和比较。
移码 : 补码的符号位取反
浮点数的表示是采用尾数+阶码的方式表示, N=M*2^E, 其中阶数E采用移码表示。
移码的表示方法是:
[+1] = [0001]原 = [0001]反 = [0001]补 = [1001]移
[-1] = [1001]原 = [1110]反 = [1111]补 = [0111]移