用于半监督的图扩散网络笔记

news2025/2/28 21:10:09

1 Title

Graph Neural Diffusion Networks for Semi-supervised Learning（Wei Ye, Zexi Huang, Yunqi Hong, and Ambuj Singh）【2022】

2 Conclusion

This paper proposes a new graph neural network called GND-Nets (for Graph Neural Diffusion Networks) that exploits the local and global neighborhood information of a vertex in a single layer. Exploiting the shallow network mitigates the over-smoothing problem while exploiting the local and global neighborhood information mitigates the under-smoothing problem. The utilization of the local and global neighborhood information of a vertex is achieved by a new graph diffusion method called neural diffusions, which integrate neural networks into the conventional linear and nonlinear graph diffusions.

3 Good Sentences

1、Graph Convolutional Networks (GCN) is a pioneering model for graph-based semi-supervised learning. However,GCN does not perform well on sparsely-labeled graphs. Its twolayer version cannot effectively propagate the label information to the whole graph structure (i.e., the under-smoothing problem)while its deep version over-smoothens and is hard to train
(i.e., the over-smoothing problem).(The problems of previous GCN methods meet)
2、JK-Nets proposes to aggregate the output of each layer by skipping connections.
It selectively exploit information from neighborhoods of different locality. Indeed, the performance of GCN is improved by aggregating the output of each layer, but not significantly. One reason is that the deep GCN model with many graph convolutional layers is hard to train.（The reason why previous improvements of GCN only had little role）
3、Differing from traditional linear graph diffusions such as the personalized PageRank diffusion and the heat kernel diffusion, the weighting parameters in neural diffusions are not fixed but learned by neural networks, which makes neural diffusions adaptable to different datasets.（The advantages of GND-Nets expect exploiting the shallow network mitigates the over- smoothing problem while exploiting the local and global neighborhood information mitigates the under-smoothing problem）
4、Considering that the multiplication of matrices in Eqn. (1) has a high time complexity (O(n^2)) and the eigendecomposion of L is prohibitively expensive (O(n^3)) especially for large
graphs, we can circumvent the problem by approximating gθ by a truncated expansion in terms of Chebyshev polynomials T_k(x) up to the K-th order.（The solution of the problem of excessive time complexity）

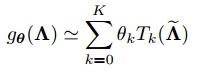图卷积：，其中x∈ $R^n$ 是顶点上的信号（特征向量）， $g_\theta$ 是 $\Lambda$ 上的光谱滤波器，由θ∈ $R^n$ 参数化， $U^Tx$ 是信号x的图形傅里叶变换。这个公式的时间复杂度比较大 $O(n^3)$ ,可以通过用切比雪夫多项式 $T_k(x)$ 直到K阶的截断展开式逼近 $g_\theta$ 来解决这个问题:, $\tilde{\Lambda }=\frac{2}{\lambda _{max}}\Lambda -I$ , $\lambda _{max}$ 是 $L$ 的最大特征值,θ ∈ $R^K$ 是切比雪夫系数的向量，那么图卷积公式可以写成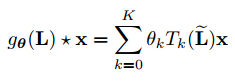：，这个公式是K局部化的，即，它仅依赖于与中心顶点相距最大K跳距离的顶点（K阶邻域），其时间复杂度为O(e)，e是图的边数。

通过设置K = 1和λmax = 2，GCN简化了方程:，再通过设置 $\theta =\theta _0 =- \theta _1$ 并使用 $L_{sym}$ ，公式可以被改写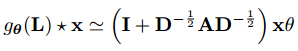为：，因为的范围在0~2之间，重复这一学习规则将导致深度神经网络中的数值不稳定性和爆炸/消失梯度问题。为了解决这个问题，GCN使用了一种重正化技巧：，把范围变成了-1~1。

这样就可以把上面的公式推广到图中所有顶点上的信号矩阵X：，其中θ∈ $R^{d \times r}$ 是滤波器参数矩阵，r是顶点特征向量上的滤波器数量。

然后，GCN的分层传播规则被定义如下: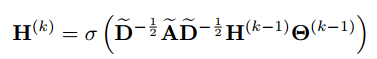

其中 $H^{(0)}$ = X， $\Theta ^{k-1}$ 是第k-1层中的可训练滤波器参数矩阵，σ（ $\cdot$ ）是激活函数。

图扩散方法，就是将标签信息传播到整个图结构。具体来说，假设顶点标签满足同向性原则即彼此连接的顶点很可能具有相同的标签。

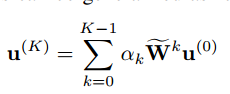其中 $u^{(0)}$ 是长度为n（顶点数）的向量，其每一项表示每个顶点处的初始材质。 $\alpha _k$ 是非负的，它满足滑 $\sum _k\alpha _k=1$ ，并作为衰减权重来确保扩散消散。 $u^{(K))}$ 捕获在图形边缘的扩散。

如果，那么上式为PageRank扩散。如果，那么为热核扩散。

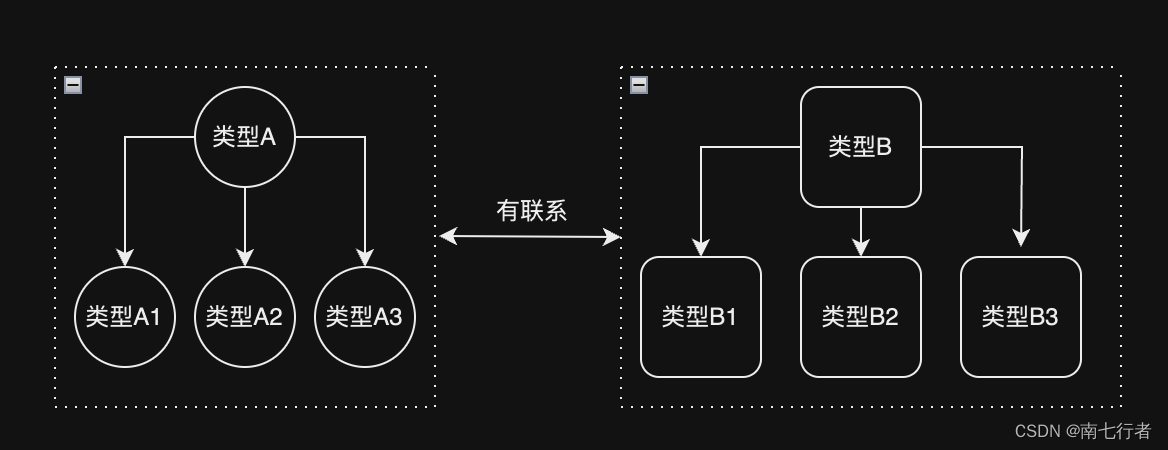
Local and Global Neighborhood Information

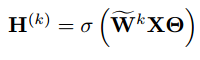本文(1)将所有中间非线性激活函数设为线性激活函数σ(x) =x，（2）用 $\tilde{W}=\tilde{D}^{-1}\tilde{A}$ 替代 $\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}$ (3)将所有权重矩阵重新参数化为单个矩阵。这样，GCN的分层传播公式就变成了，可以被认为是通过在顶点特征矩阵x上应用linear层（由θ参数化）来计算的，对于每个列向量z， $z\in Z$ ，如果图结构是非二部图，那么通过多次迭代向量会收敛，其极限值将是矩阵W的主要特征向量。

这个定理表明：如果 k 非常大且 λ1 > λ2 > ... > λn，其中 λ1 到 λn 是矩阵的特征值，那么矩阵的每一列特征都会收敛到矩阵的主要特征向量 u1，而不考虑矩阵 X 和 Θ。其中 X 是输入特征矩阵，Θ 是参数矩阵。也就是说当 k 很大时，GCN 模型会倾向于收敛到矩阵 W 的主要特征向量，而忽略了输入特征矩阵 X 和参数矩阵 Θ 的影响，从而导致模型性能下降。

这在分类方面来说基本没什么用，但在收敛过程中产生的中间向量可能比较有用。比如下图，k=10000时分不出类了，但k=19的中间向量还是比较好分类的。在这个过程中，没有使用标签信息来指导学习。如果图结构的拉普拉斯矩阵捕获了成对顶点的相似性，即，图满足同向性原理，则幂迭代将使聚类分离，并且所提供的标签信息将加速该过程

Neural Diffusions：

GCN仅使用一次幂迭代（k = 1），这不足以在标记顶点数量稀少时将标记信息传播到整个图结构。本文使用k = K次幂迭代来生成中间矩阵序列，本文建议将这些矩阵中包含的所有局部和全局邻域信息聚合在一个层中，用于稀疏标记图上的半监督分类。聚合是通过单层感知器（SLP）等神经网络实现的，

SLP的聚合定义为：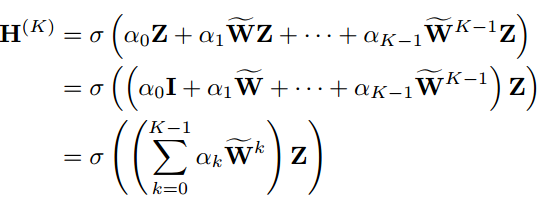

是SLP的加权参数。

之前的公式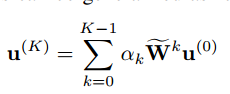是截断图扩散，而通过放松约束，允许 $\alpha _k$ 为任意值并让SLP自适应地学习它们，就得到了一种新的图扩散方法:神经扩散。

实现的时候要注意：首先展平 W^kZ (0 ≤ k ≤ K − 1) 成为向量，并且考虑把维度跃迁作为特征属性。最后使用SLP来聚合所有这些K向量。由于SLP的滤波器数量设置为1，需要通过 $f^{-1}$ 将SLP的输出整形为矩阵 $H(K) \in R^{n \times r}$ ,其维数与z相同。 $H^{(K)}$ 是一种线性图扩散。