题目描述
围棋棋盘由纵横各19条线垂直相交组成,棋盘上一共19 x 19 = 361 个交点,
对弈双方一方执白棋,一方执黑棋,落子时只能将棋子置于交点上。
“气”是围棋中很重要的一个概念,某个棋子有几口气,是指其上下左右方向四个相邻的交叉点中,
有几个交叉点没有棋子,由此可知:
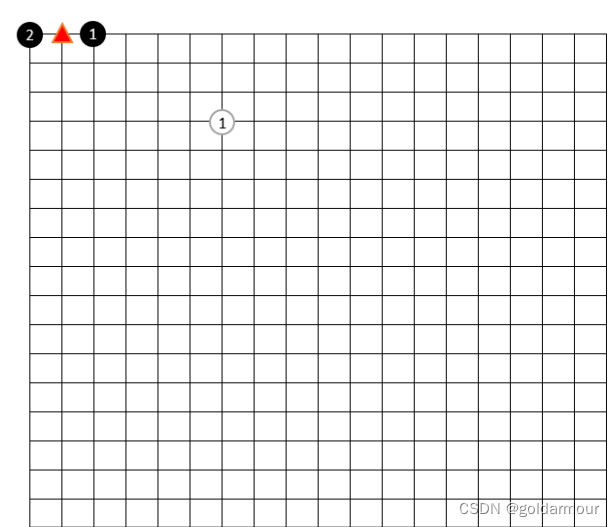
1.在棋盘的边缘上的棋子最多有 3 口气(黑1),在棋盘角点的棋子最多有2口气(黑2),
其他情况最多有4口气(白1)
2.所有同色棋子的气之和叫做该色棋子的气,需要注意的是,同色棋子重合的气点,对于该颜色棋子来说,只能计算一次气,比如下图中,黑棋一共4口气,而不是5口气,因为黑1和黑2中间红色三角标出来的气是两个黑棋共有的,对于黑棋整体来说只能算一个气。
3.本题目只计算气,对于眼也按气计算,如果您不清楚“眼”的概念,可忽略,按照前面描述的规则计算即可。
现在,请根据输入的黑棋和白棋得到坐标位置,计算黑棋和白棋一共各有多少气?
输入描述
输入包含两行数据,如:
0 5 8 9 9 10
5 0 9 9 9 8
【华为OD机试】围棋的气【C卷|100分】
news2026/2/15 23:31:37
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1597037.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
2024-04-15_[UPnP]:详细解析
UPnP
一、论文阅读
1.2 Theory
1.2.1 Geometry of the absolute pose problem α i f i v i R p i t , i 1.. n . \alpha_i \mathbf{f}_i \mathbf{v}_i \mathbf{R} \mathbf{p}_i \mathbf{t} ,i1..n. αifiviRpit,i1..n. 其中: P i ∈ R 3 P_i \i…
直播平台主播的美颜功能是如何实现的?美颜SDK技术深度解析
时下,直播平台的美颜SDK则扮演着至关重要的角色。接下来,我们将深入探讨直播平台主播美颜功能的实现原理,以及美颜SDK技术的应用。
一、美颜技术的发展
随着人工智能和计算机视觉技术的不断进步,美颜技术逐渐实现了更加智能化的…
如何在横向渗透攻击中寻到一线生机
横向渗透,作为计算机网络中的一种攻击技术,展现出了攻击者如何巧妙地利用同一级别系统间的漏洞和弱点,扩大其网络访问权限。与纵向渗透不同,横向渗透不关注权限的垂直提升,而是更侧重于在同一层级内扩展影响力。
横向…
Problem #8 [Easy]
This problem was asked by Google.
A unival tree (which stands for “universal value”) is a tree where all nodes under it have the same value.
Given the root to a binary tree, count the number of unival subtrees.
For example, the following tree has 5 un…
强烈推荐 ——电脑终端管理系统
强烈推荐!电脑终端管理系统
电脑终端管理系统使用的目的是为了管控电脑上硬件和软件资产,以及员工使用电脑的行为,最终目的是为了保护企业资产和信息,以下是一些推荐的电脑终端管理系统,这些系统为企业提供了强大的功…
OpenHarmony南向开发案例:【智能体重秤】
一、简介
本demo基于OpenHarmony3.1Beta版本开发,该样例能够接入数字管家应用,通过数字管家应用监测体重秤上报数据,获得当前测量到的体重,身高,并在应用端形成一段时间内记录的体重值,以折线图的形式表现…
破译验证码reCAPTCHA 之 打码平台
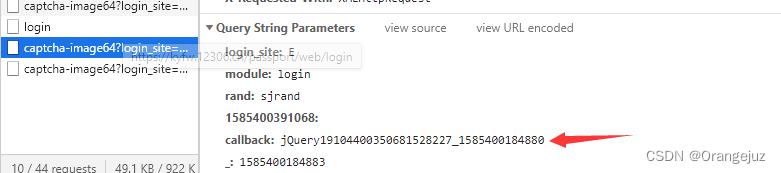
由于登录需要验证码,除了日常的字符串+数字,此时就需要用第三方插件进行破译。 reCaptcha是Google公司的验证码服务,方便快捷,改变了传统验证码需要输入n位失真字符的特点。 1. reCAPTCHA 初识
reCaptcha是Google公司…
Python数据可视化库—Bokeh与Altair指南【第161篇—数据可视化】
👽发现宝藏 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【点击进入巨牛的人工智能学习网站】。 在数据科学和数据分析领域,数据可视化是一种强大的工具,可以帮助我们…
实用VBA:19.Excel一键修复文件链接
1.需求场景 此前与大家分享过一键提取文件目录和文件名的方法,并且VBA中加一句语句就可以使提取出来的文件名带有链接,这样很方便在对大量文件进行检查时不必在资源管理器里到处翻目录,所见即所得,点击文件名即可打开文件。是个实…
Python爬虫与数据可视化论文课题免费领取咨询
引言
作为一名在软件技术领域深耕多年的专业人士,我不仅在软件开发和项目部署方面积累了丰富的实践经验,更以卓越的技术实力获得了🏅30项软件著作权证书的殊荣。这些成就不仅是对我的技术专长的肯定,也是对我的创新精神和专业承诺…
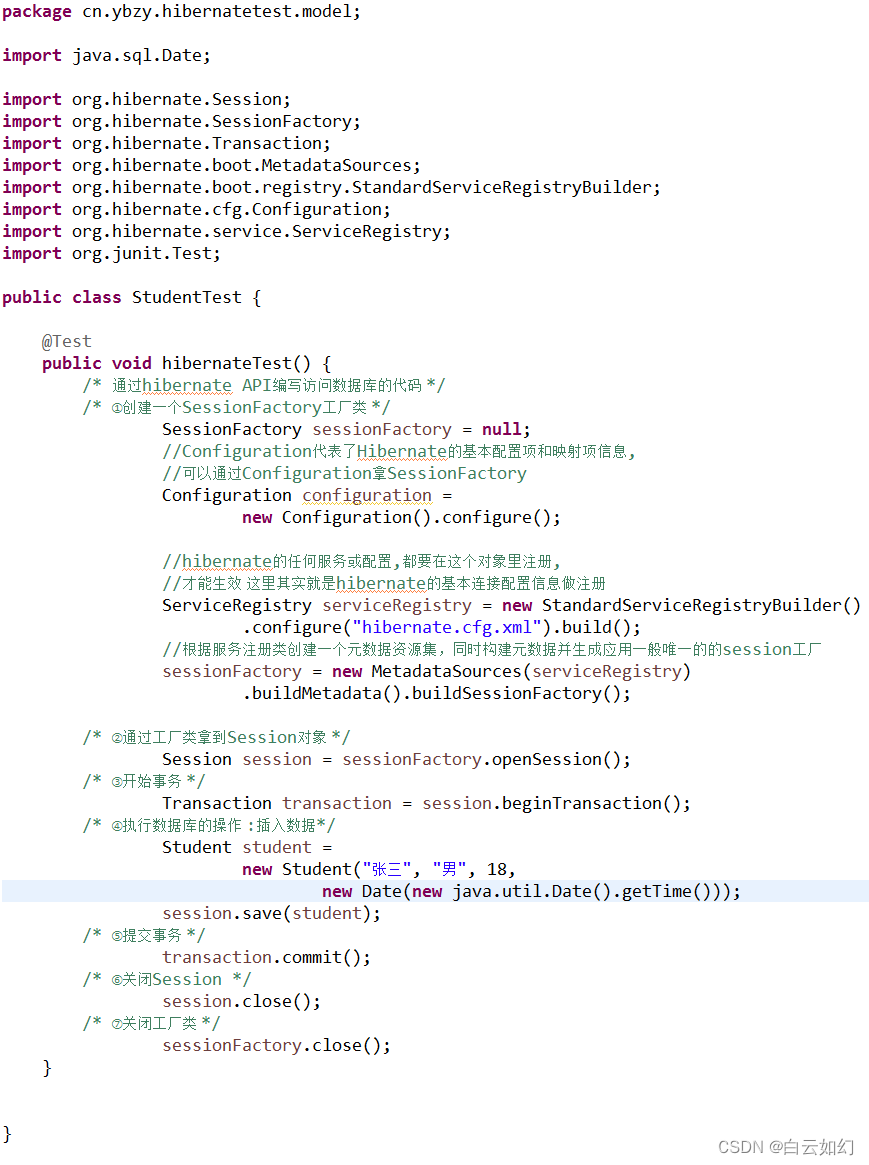
快速实现一个Hibernate的例子
写第一个简单的Hibernate程序:
具体的开始第一个Hibernate程序之前: 找到jar包, hibernate 的核心包, mysql数据库的连接驱动包, junit测试包
①创建Hibernate配置文件 ②创建持久化类
也是和数据库中数据表一一对应这个类 ③创建对象-关系映射文件 ④通过hibern…
面向对象——继承、多态、方法重写、构造方法重载简单例子
说明: 这学期开了面向对象的课程,老师上星期布置了作业,之前用JAVA写了一遍,今天心血来潮又用C写了一遍。博主只会敲代码,但面向对象是小白一个,欢迎交流学习。
题目: C代码:
#inc…
【Qt 学习笔记】Qt常用控件 | 按钮类控件Radio Button的使用及说明
博客主页:Duck Bro 博客主页系列专栏:Qt 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ Qt常用控件 | 按钮类控件Radio Button的使用及说明
文章编号ÿ…
[docker] 核心知识 - 容器/镜像的管理和操作
[docker] 核心知识 - 容器/镜像的管理和操作
想要查看完整的指令,可以通过 docker --help 列举所有的指令,这里会提到一些比较常用的核心指令
查看容器的状态
这个应该是最常用的指令,语法为 docker ps, ps 为 process status …
华为欧拉系统(openEuler-22.03)安装深信服EasyConnect软件(图文详解)
欧拉镜像下载安装
iso镜像官网下载地址
选择最小化安装,标准模式
换华为镜像源
更换华为镜像站,加速下载:
sed -i "s#http://repo.openeuler.org#https://mirrors.huaweicloud.com/openeuler#g" /etc/yum.repos.d/openEuler.r…
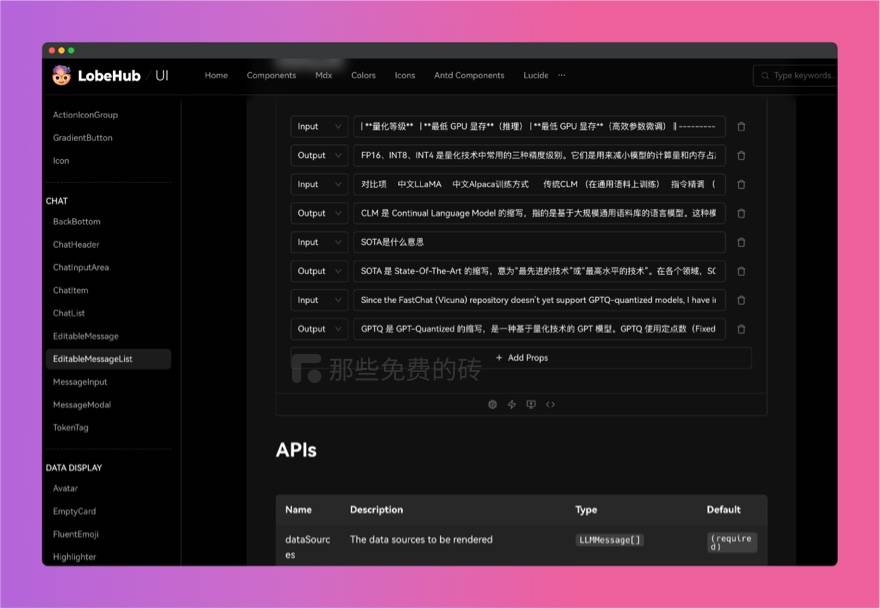
Lobe UI - 基于 AntDesign 开发的 AIGC Web 应用的开源 UI 组件库
今天推荐一个可以快速开发 ChatGPT UI 界面的组件库,质量很高,拿来就能用。
Lobe UI 是由 lobehub 团队开发的一套 web UI 组件库,和我之前推荐的很多通用型的 UI 组件库不同,Lobe UI 是专门为目前火热的 AIGC 应用开发而打造&am…



![Problem #8 [Easy]](https://img-blog.csdnimg.cn/direct/8e3470409369490b923d625980bc87d9.png)





![[docker] 核心知识 - 容器/镜像的管理和操作](https://img-blog.csdnimg.cn/direct/ead44bb2cd9047d7a10afe6786fb4732.gif#pic_center)