💓博主CSDN主页:麻辣韭菜💓
⏩专栏分类：C++知识分享⏪
🚚代码仓库:C++高阶🚚
🌹关注我🫵带你学习更多C++知识
🔝🔝
前言
前面我们实现了AVL树，发明AVL树的人是天才，那发明红黑树的人就是天才中天才。
AVL由于加入平衡因子，所以对树的平衡过于严格。这就导致了频繁的旋转。从而增加时间复杂度。这也是为什么map和set底层的封装没有用AVL树，而是用的红黑树！！！
一、红黑树的概念
红黑树
，是一种
二叉搜索树
，但
在每个结点上增加一个存储位表示结点的颜色，可以是
Red
或
Black
。 通过对
任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路
径会比其他路径长出俩倍
，因而是
接近平衡
的。
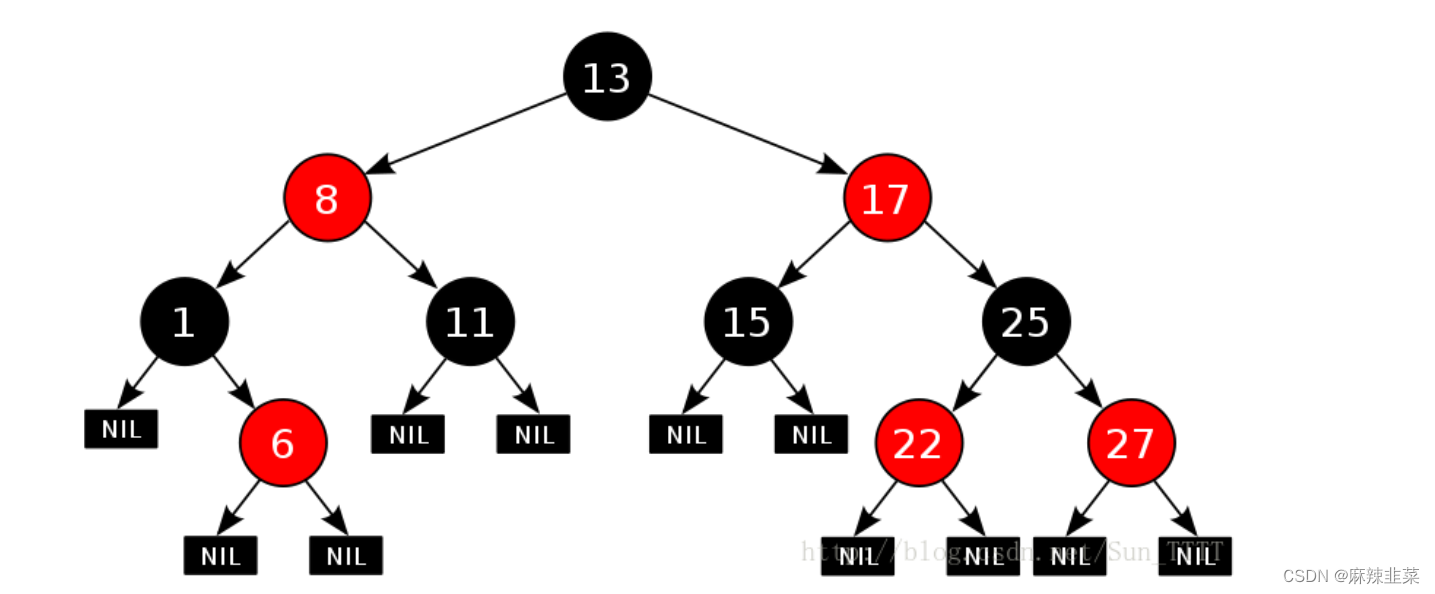
二、红黑树的性质
1. 每个结点不是红色就是黑色2. 根节点是黑色的3. 如果一个节点是红色的，则它的两个孩子结点是黑色的4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均 包含相同数目的黑色结点5. 每个叶子结点都是黑色的 ( 此处的叶子结点指的是空结点 )
三、红黑树节点的定义
enum Color //颜色
{
RED,
BLACK,
};
template<class T, class V>
struct RBTreeNode
{
RBTreeNode<T, V>* _left; //左孩子
RBTreeNode<T, V>* _right; //右孩子
RBTreeNode<T, V>* _parent; //父亲
pair<T, V> _kv;
Color _col;
RBTreeNode(const pair<T, V>& kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(kv)
, _col(RED) //为什么默认是红色？根节点必须是黑色，这就意味着默认给黑色那么调整次数就会变多。
{}
};利用节点这个类，我们再定义红黑树类 。
template <class T, class V>
class RBTree
{
typedef RBTreeNode<T, V> Node; //节点名字太长 重新命名
private:
Node* _root;
};四、红黑树插入
插入的代码这里细节，从搜索二叉树到AVL树，都是一样的。
bool Insert(const pair<T, V>& kv)
{
if (_root == nullptr) //判断是不是第一次
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
//判断k的值是大于还是小于父亲的k值
if (parent->_kv.first > kv.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
}
因为
新节点的默认颜色是红色
，因此：如果
其双亲节点的颜色是黑色，没有违反红黑树任何
性质
，则不需要调整；但
当新插入节点的双亲节点颜色为红色时，就违反了性质三不能有连
在一起的红色节点
，此时需要对红黑树分情况来讨论：
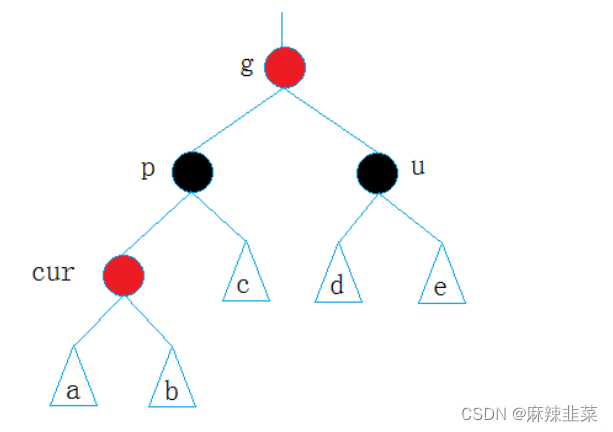
约定:cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点
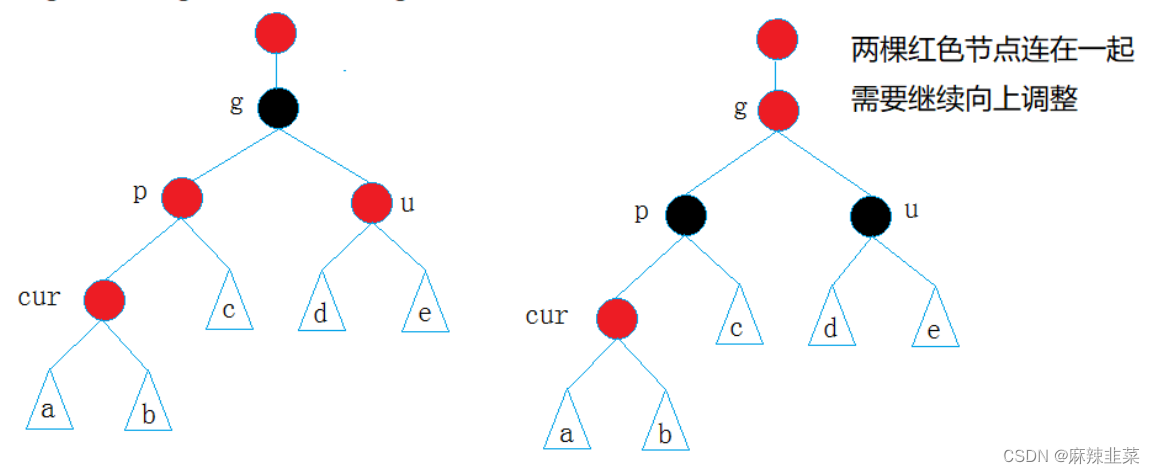
情况一: cur为红，p为红，g为黑，u存在且为红
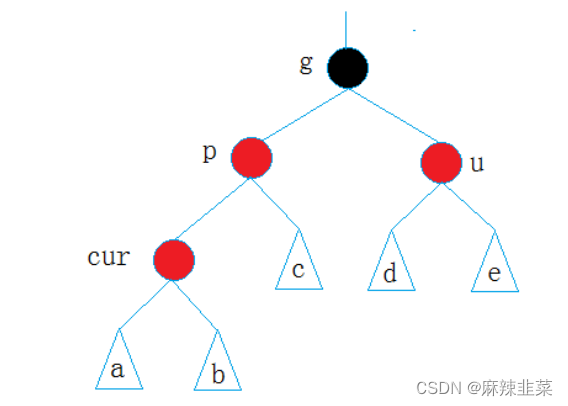
- 如果g是根节点，调整完成后，需要将g改为黑色
- 如果g是子树，g一定有双亲，且g的双亲如果是红色，需要继续向上调整
情况二: cur为红，p为红，g为黑，u不存在/u存在且为黑
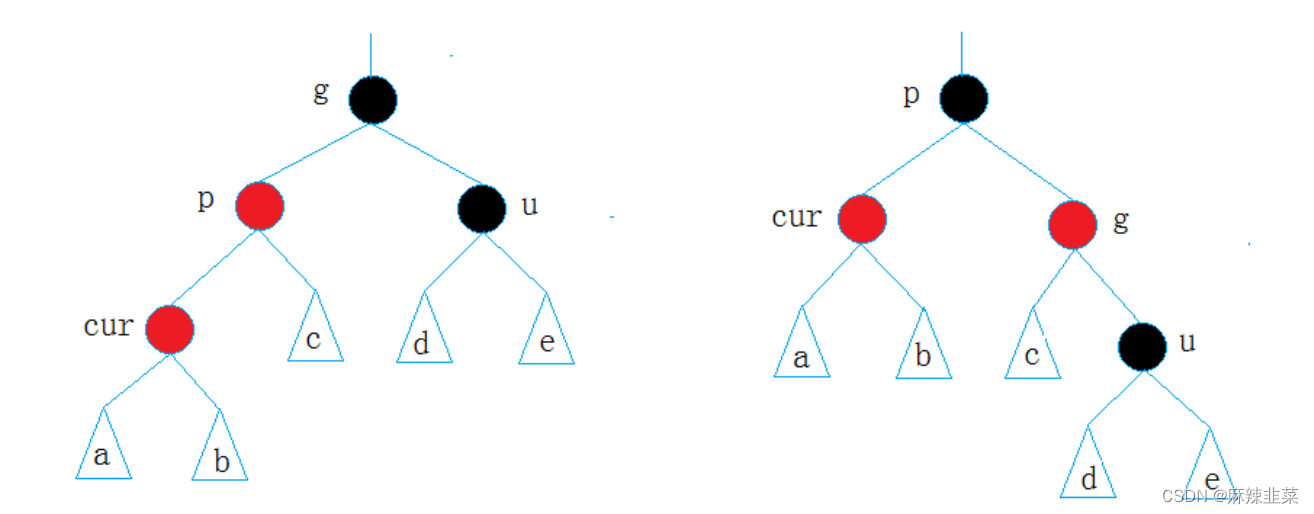
说明:u的情况有两种
1.如果u节点不存在，则cur一定是新插入节点，因为如果cur不是新插入节点则cur和p一定有一个节点的颜色是黑色，就不满足性质4:每条路径黑色节点个数相同。
2.如果u节点存在，则其一定是黑色的，那么cur节点原来的颜色一定是黑色的现在看到其是红色的原因是因为cur的子树在调整的过程中将cur节点的颜色由黑色改成红色。
p为g的左孩子，cur为p的左孩子，则进行右单旋转;相反p为g的右孩子，cur为p的右孩子，则进行左单旋转p、g变色--p变黑，g变红
情况三: cur为
p
为
g
的左孩子，
cur
为
p
的右孩子，则针对
p
做左单旋转；相反，
p
为
g
的右孩子，
cur
为
p
的左孩子，则针对
p
做右单旋转
则转换成了情况2
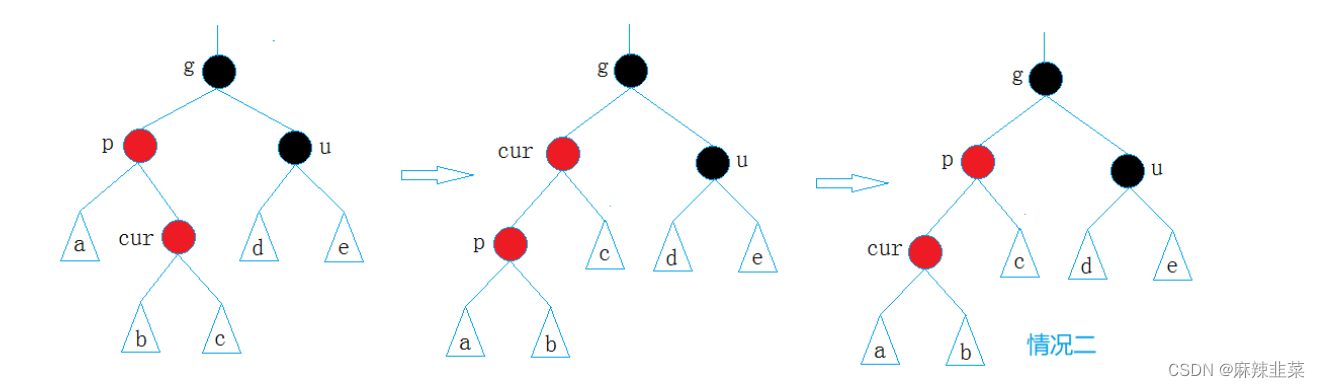
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (grandfather->_left == parent)
{
Node* uncle = grandfather->_right;
// 情况1：u存在且为红，变色处理，并继续往上处理
if (uncle && uncle->_col == RED)
{
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
// 继续往上调整
cur = grandfather;
parent = cur->_parent;
}
else // 情况2+3：u不存在/u存在且为黑，旋转+变色
{
// g
// p u
// c
if (cur == parent->_left)
{
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
// g
// p u
// c
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
//parent->_col = RED;
grandfather->_col = RED;
}
break;
}
}
else // (grandfather->_right == parent)
{
// g
// u p
// c
Node* uncle = grandfather->_left;
// 情况1：u存在且为红，变色处理，并继续往上处理
if (uncle && uncle->_col == RED)
{
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
// 继续往上调整
cur = grandfather;
parent = cur->_parent;
}
else // 情况2+3：u不存在/u存在且为黑，旋转+变色
{
// g
// u p
// c
if (cur == parent->_right)
{
RotateL(grandfather);
grandfather->_col = RED;
parent->_col = BLACK;
}
else
{
// g
// u p
// c
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return true;
}关于旋转不懂的，你可以去看之前的C++ AVL树底层实现原理。关于验证红黑树，大家感兴趣的可以去我码云看完整代码！！！
