---

前言

不管是幅度调制还是角度调制，都离不开正弦信号，其中相干解调都要求恢复发送端使用的正弦载波信号，这一节就来深入探究一下载波同步的相关知识。

---

一、正弦信号

在通信原理中，正弦信号一般写作$\cos 2\pi f_{c}t$。（正弦余弦只是相位不同，没有本质区别）这个信号是由振荡器产生的，由于振荡器的不稳定性，实际生成信号的相位会有微小的偏移$\theta (t)$，由于这个变化一般比较慢，就近似成一个常数相位偏移，从而有：

$\cos (2\pi f_{c}t+\theta )$

这里的相偏$\theta$是个随机变量，不同的震荡器在不同的时间可能会有不同的相偏。

二、载波同步

之前在介绍相干解调时提过，如果接收端不使用发送端相同的载波，即使解调用载波与调制用的载波频率相同，其随机相偏也不相同，最终解调出来的信号是$m(t)\cos (\theta -\varphi )$，导致无法恢复出原信号。

因此，相干解调必须使用频率相偏都与发送端一致的载波，所以需要进行载波同步，也叫载波恢复。对于发送端直接插入了载波一同发射的调制，只需要在接收端直接用窄带滤波器滤出使用即可。下面我们重点介绍一下发送端没有发送载波信号时的载波同步方法。

2.1、平方环法

对于没有发送载波的已调信号，则需要其他的方法恢复载波，其中一种方法是平方环法，其框图如下：

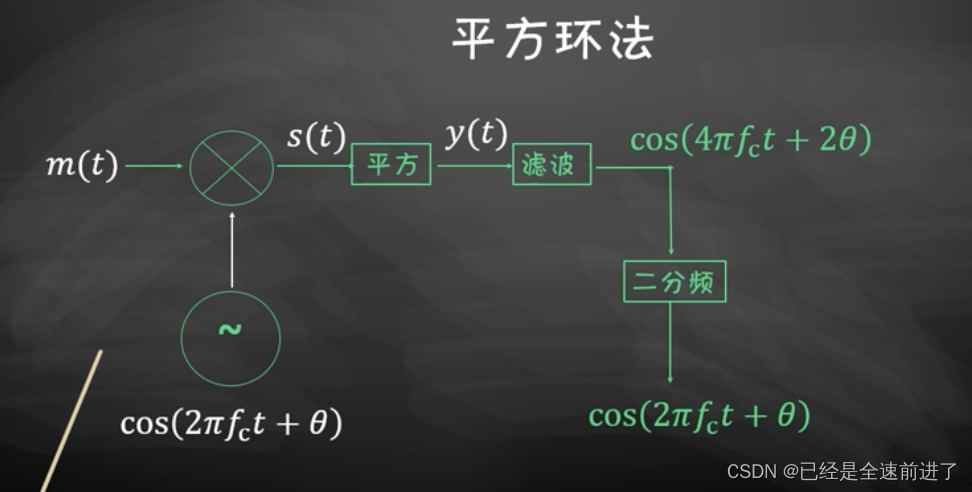
当我们说已调信号中不包含载波，是指$s(t)=m(t)\cos (2\pi f_{c}t+\theta )$中不包含载波频率处的冲激，也即$m(t)$的均值为0。平方环法则首先将输入信号求平方，从而得到：

$s^2(t)=m^2(t){\cos }^2(2\pi f_{c}t+\theta )$
$=\frac{1}{2}\left[m^2(t)+m^2(t)\cos (4\pi f_{c}t+2\theta )\right]$

观察上式，可以发现右边的部分就是用载波频率为$2f_c$的正弦载波对基带信号$m^2(t)$做双边带调制。问题的关键是，$m^2(t)$的均值是否为0，如果其均值不为零，则包含直流分量，对应的频谱则包含零频冲激，经过载波搬移后即变成载波处的冲激$\cos (4\pi f_{c}t+2\theta )$。

$m(t)$的均值为0，且我们假设$m(t)$为基带信号，带宽有限，则其在时域无限。那么$m(t)$就必然是一个有正有负的信号。因此，$m^2(t)$的均值必然会大于$m(t)$的均值，也就是大于0，因此$m^2(t)$含有直流分量，我们也就可以通过窄带滤波获得两倍频的载波分量$\cos (4\pi f_{c}t+2\theta )$，再通过一个二分频模块，讲频率变为原本的一半，即可恢复出原始载波。

2.2、科斯塔斯环法（castas）

科斯塔斯环法则是通过在接收端使用振荡器生成与发送端同频同相的载波信号进行解调。同频很容易，只要知道发送端用的是什么频率即可，然而同相却没有那么简单，因为相偏$\theta$是随机的。

如果有办法能知道接收端的载波相位与发送端的载波相位的大小关系，并且接收端可以调整其相位，从而达到与发送端同相端话，就可以实现载波恢复了。这就是科斯塔斯环法的设计思路。其具体框图如下：

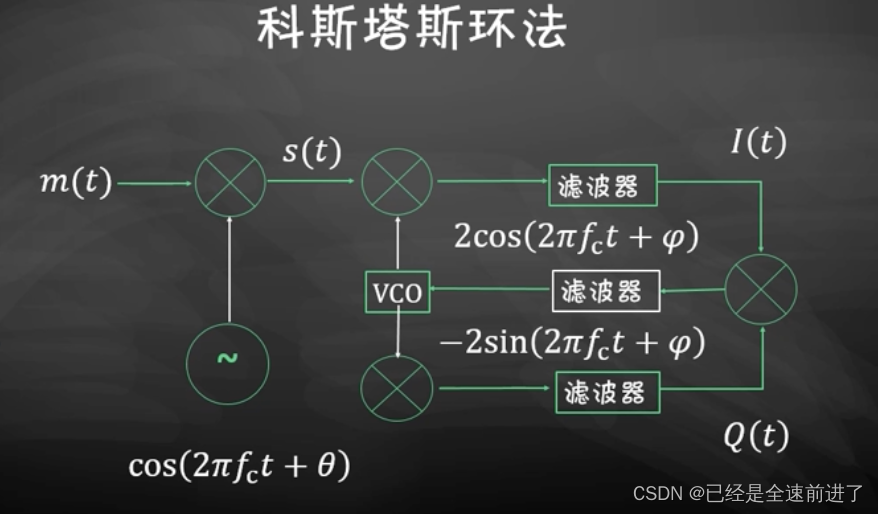
其中VCO为用来生成正弦信号的压控振荡器，其生成两个载波信号$\cos (2\pi f_{c}t+\varphi ),\sin (2\pi f_{c}t+\varphi )$。接着，使用两个载波信号分别对接收信号进行解调，即上图中的I,Q两路。分别得到解调后的信号$m(t)\cos (\theta -\varphi )$,$m(t)\sin (\theta -\varphi )$，再将其乘得到$\frac{1}{2}{m}^2(t)\sin 2(\theta -\varphi )$，最后通过滤波器平滑输入振荡器。

可以看到，上式的正负完全取决于$\theta -\varphi$的取值，当$\theta -\varphi \in (0,\pi /2)$时，取值为正，该输入会调整振荡器的相位使$\varphi$增大。相反当$\theta -\varphi \in (-\pi /2,0)$时，则会减小$\varphi$。而当$\theta$和$\varphi$相等时，两路信号乘积为0，则中间的调整相位的输入变成0，VCO就会稳定在当前相位，从而最终达到与发送端载波同频同相的状态。

2.3 相位模糊

上述两种载波同步方法，都有存在载波模糊的问题。在平方环法中，如果二倍频的载波相位中多了一个$2\pi$，其信号值没有影响，而二分频之后则会得到$\cos (2\pi f_{c}t+\theta +\pi )$。而在科斯塔斯环法中，如果发送载波与解调载波相位相差恰好为$k\pi /2$时，两路信号乘积结果仍然是0，VCO也会稳定输出$\cos (2\pi f_{c}t+\theta +k\pi /2)$。

这张相位模糊问题最终会导致解调出来的信号与原信号相比幅值取成了相反数。有人会说，那简单，取回来不就行了。然而从上述相位模糊的分析不难发现，有没有发生相位模糊问题本身便是不容易察觉的，因此解调得到的信号究竟是原信号还是取了相反数之后的结果是未知的，因此相位模糊不是一个可以忽略不计的问题。

---

总结

本节是第三章模拟信号调制的最后一节，介绍了载波同步相关的知识，这对于相干解调至关重要。两种载波同步的方法原理与框图也都清晰易懂，最好都能掌握。