什么是素数（也称质数）？和合数相对。
其特点是只能被 1 和它本身 整除，无法被其他整数整除。或者公因数只有它自己和1两个数的数

怎么求解素数呢？对于求解质数的方法很多，但是有一种专门求解素数的功能：埃拉托色尼筛选法-这个程序简直就是为求解素数而生。
埃拉托色尼筛选法：埃拉托色尼筛选法（Sieve of Eratosthenes）是一个用来找出一定范围内所有素数的经典算法。这个算法是由古希腊数学家埃拉托色尼发明的。对于C语言实现的描述是：如果自然数i为素数，则设a[i]为1，否则设为0。首先把数组中所有的元素设为1，以表明这些数全部是素数。然后把数组中所有对应的索引处已证明是非素数（一直是素数的倍数）的元素设为0。如果所有的更小的素数的倍数都已经设为0,a[i]仍然为1，则可知它是素数。

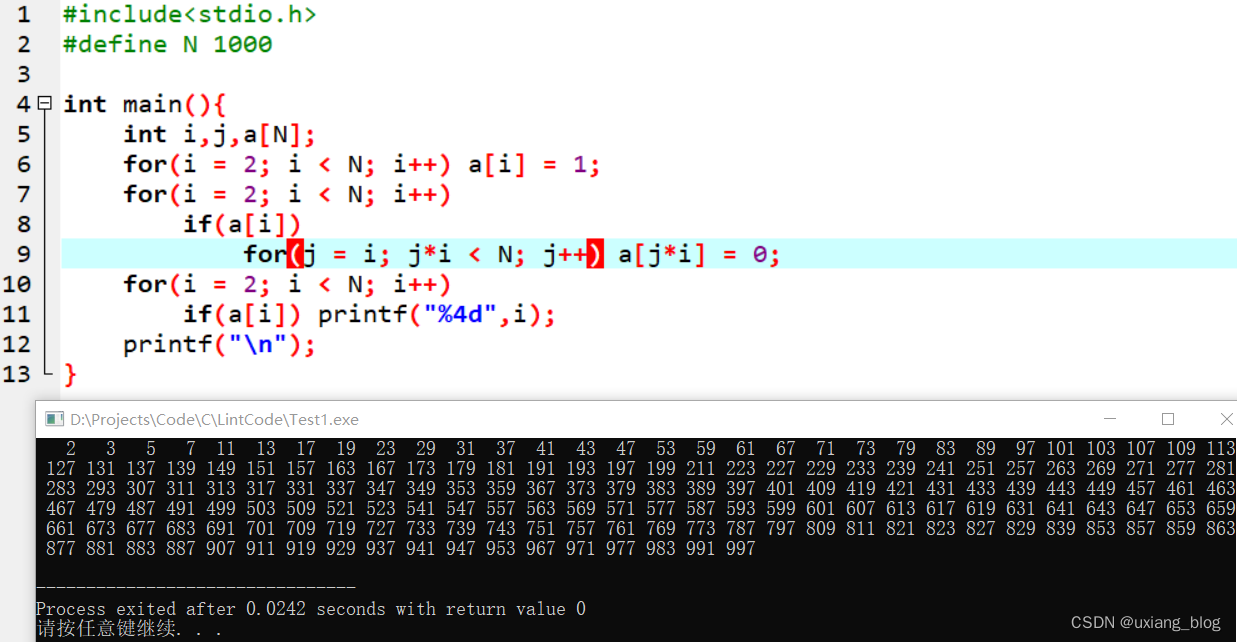
我们先从一定范围内N(N=1000)的素数开始，先写一个埃拉托色尼，然后将它打印出来：

#include<stdio.h>
#define N 1000

int main(){
	int i,j,a[N];
	for(i = 2; i < N; i++) a[i] = 1;
	for(i = 2; i < N; i++)
		if(a[i])
			for(j = i; j*i < N; j++) a[j*i] = 0;
	for(i = 2; i < N; i++)
		if(a[i]) printf("%4d",i);
	printf("\n");
}

注意到这个式子没有问题后，我们着手去实现题目3条：

• 现在通过 scanf() 函数接收一个正整数 n，判断它是否是质数：
• 若 n 是质数，通过输出语句输出 [n] is a prime number.
• 否则，输出 [n] is not a prime number.

前一条非常容易实现：

int num;
scanf("%d",&num);

后两条是两个选择，而且我们通过埃拉托色尼已经将数组中数标记为2类数字了，第一类是值为1的质数，第二类是值为0的合数。
这里我们有两种选择：

• 第一：使用if else;

	i = num;
	if(a[i]){
		printf("%d is a prime number.",i);
	}else{
		printf("%d is not a prime number.",i);
	}

• 第二：选择switch（我用的是这个）

    i = num;
    switch(a[i]){
    	case 1:printf("%d is a prime number.",i);break;
    	case 0:printf("%d is not a prime number.",i);break;
    }    

注意:我在这里犯了一个错误，那就是误以为是我们输入的数字和数组里面存储的元素比，但不是，这个里我们是和数组元素的索引比较。

完整代码如下：

#include <stdio.h>
#include <stdio.h>
#define N 1000

int main() {
    // 初始化变量
    // Write your code here
    int i,j,a[N],num;

    // 读取用户输入的数
    scanf("%d",&num);

    // 初始化数组，将所有位置都设为1
    for(i = 2; i < N; i++) a[i] = 1;

    // 遍历数组，标记非质数位置为0
    for(i = 2; i < N; i++)
        if (a[i]) 
            for(j = i; i*j < N; j++) a[i*j] = 0;

    // 判断输入数是否为质数，并输出结果
    i = num;
    switch(a[i]){
    	case 1:printf("%d is a prime number.",i);break;
    	case 0:printf("%d is not a prime number.",i);break;
    }    
}

我们测试一下：分别输入4、5（最大能测试999，因为数组下标是从0开始的,数组长度为1000，a[2]~a[999]）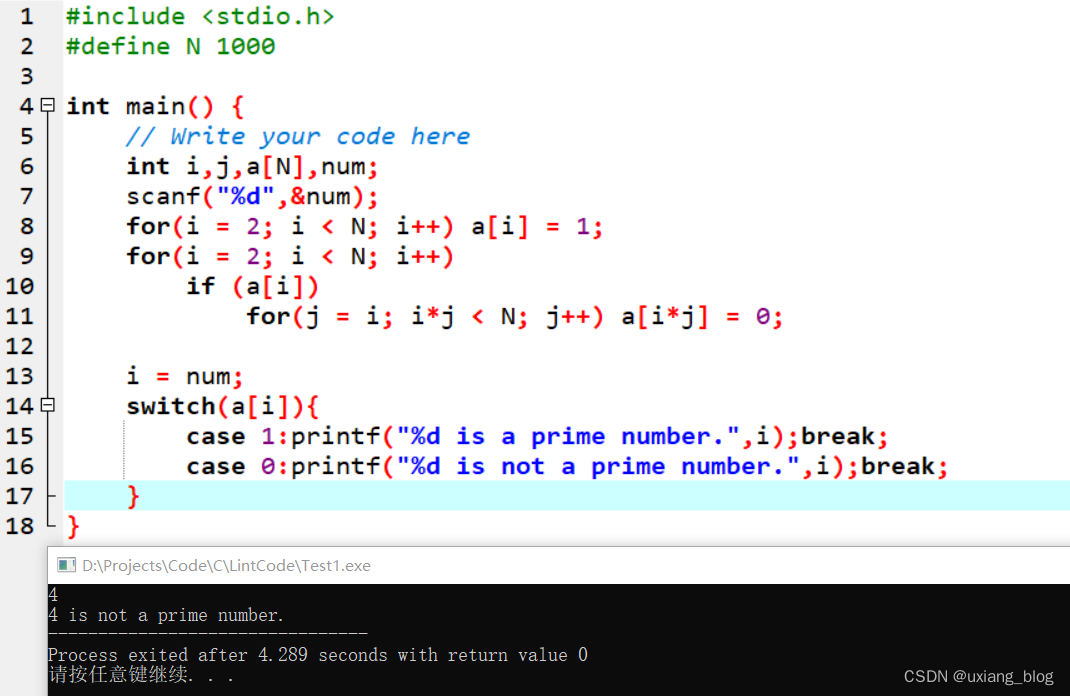


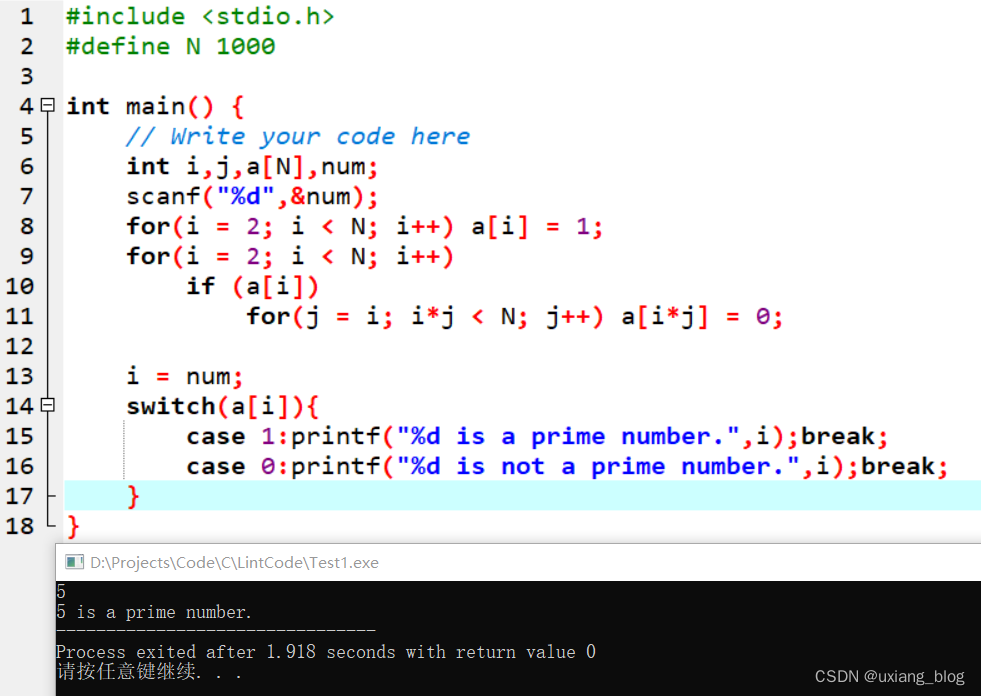
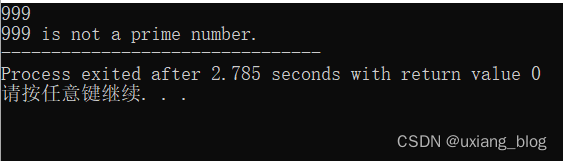
但是这个依然不符合题目要求：2<=num<=10^5，只要将N修改到100000就超时了。
数据类型的范围点击跳转

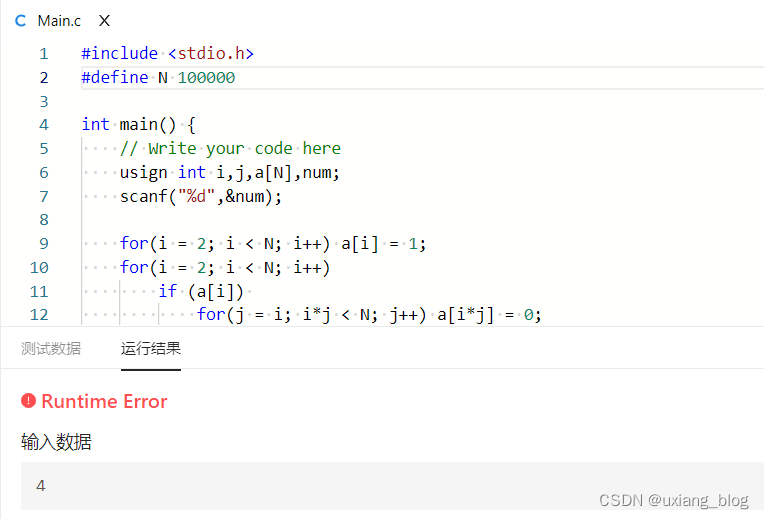
理论上随着要求数据的增大只要修改N的值兼顾i,j,a[i]的数据类型就可以了,但是那将需要太多的内存（例如，int a[100000]; 会占用近 4MB 的内存，这在大多数现代系统上是可以接受的，但不是一个好的做法，尤其是如果你打算同时处理多个这样的数组时）。我们需要一个通用的方法，我们需要更加智能的办法。

接下来我们将在埃拉托色尼上加点料，让它更加智能——数组的动态存储分配：通过stdlib.c的库函数malloc，在执行时利用该值为数组动态分配空间。

#include <stdlib.h>
int main(int argc,char *argv[]) {
    long int i,j,N = atol(argv[1]);
    int *a = malloc(N*sizeof(int));
    if (a == NULL)
    	{ printf("Insufficient memory.\n"); return;	}
    

加入之后的代码如下：

#include <stdio.h>
#include <stdlib.h>


int main(int argc,char *argv[]) {
    // 从命令行参数中获取N的值，并将其转换为长整型
    // Write your code here
    long int i,j,N = atol(argv[1]),num;
    // 动态分配一个大小为N的整型数组a
    int *a = malloc(N*sizeof(int));
    // 如果分配失败，则输出错误信息并退出程序
    if (a == NULL)
    	{ printf("Insufficient memory.\n"); return;	}

    // 从标准输入读取一个整数到变量num
    scanf("%d",&num);
    // 将数组a的第2到第N-1个元素都初始化为1
    for(i = 2; i < N; i++) a[i] = 1;
    // 遍历数组a的第2到第N-1个元素
    for(i = 2; i < N; i++)
        // 如果当前元素为1
        if (a[i]) 
            // 则将数组a中从i开始，以i为公倍数的元素都置为0
            for(j = i; i*j < N; j++) a[i*j] = 0;

    // 将变量num的值赋给i
    i = num;
    // 根据数组a中i位置的值判断num是否为质数，并输出相应的结果
    switch(a[i]){
    	case 1:printf("%d is a prime number.",i);break;
    	case 0:printf("%d is not a prime number.",i);break;
    } 
    // 程序结束，返回0
	return 0;   
}

测试之后结果超时了

哈哈哈，炫酷了一把，结果还是没有解决，但这种思考让我收获匪浅，留一个悬念，有时间了再研究研究，今天就到这里。
下面有个写得不错的，代码如下：

#include <stdio.h>

/**
 * @brief 判断一个整数是否为质数
 *
 * 读取用户输入的整数，判断该整数是否为质数，并输出相应的结果。
 *
 * @return 程序执行状态码，0 表示执行成功，其他值表示执行失败
 */
int main() {
    // 定义一个整数变量num
    // Write your code here
    int num;
    // 定义一个整数变量isPrime，用于表示是否为质数，初始值为1（是质数）
    int isPrime = 1;
    // 从标准输入读取一个整数赋值给变量num
    scanf("%d",&num);
    // 如果num等于1
    if(num==1){
        // 输出1是质数
        printf("%d is a prime number.\n",num);
    }
    // 从2开始循环到num-1
    for(int i=2;i<num;i++){
        // 如果num能够被i整除
        if(num%i==0){
            // 输出num不是质数
            printf("%d is not a prime number.\n",num);
            // 将isPrime设置为0，表示num不是质数
            isPrime = 0;
            // 跳出循环
            break;
        }
    }
    // 如果isPrime仍然为1，即num是质数
    if(isPrime){
        // 输出num是质数
        printf("%d is a prime number.\n",num);
    }
}