Lesson2: 算法的时间复杂度和空间复杂度

【本节目标】

1. 算法效率

2. 时间复杂度

3. 空间复杂度

4. 常见时间复杂度以及复杂度 oj 练习

1.算法效率

1.1 如何衡量一个算法的好坏

如何衡量一个算法的好坏呢？比如对于以下斐波那契数列：

long long Fib(int N)
{
 if(N < 3)
 return 1;
 
 return Fib(N-1) + Fib(N-2);
}

斐波那契数列的递归实现方式非常简洁，但简洁一定好吗？那该如何衡量其好与坏呢？

当计算斐波那契数列时，使用递归的方法会导致计算量呈指数级增长，效率较低。这是因为在递归计算中会重复计算相同的子问题，造成了资源的浪费。

举个例子，我们来计算斐波那契数列的第n项，假设n=5。斐波那契数列的递归定义为：

如果我们采用递归的方式计算F(5)，会涉及到很多重复计算，导致效率低下。示例代码如下：

#include <stdio.h>

int fibonacci_recursive(int n) {
    if (n == 0) {
        return 0;
    } else if (n == 1) {
        return 1;
    } else {
        return fibonacci_recursive(n-1) + fibonacci_recursive(n-2);
    }
}

int main() {
    int n = 5;
    int result = fibonacci_recursive(n);
    printf("The %dth Fibonacci number is: %d\n", n, result);
    return 0;
}

在这个例子中，计算F(5)时会重复计算F(3)、F(2)等子问题，导致效率低下。因此，为了提高效率，我们可以考虑使用其他方法，如动态规划或迭代方法来计算斐波那契数列。

如果是算阶乘

#include <stdio.h>

int factorial(int n) {
    if (n == 0) {
        return 1;
    } else {
        return n * factorial(n - 1);
    }
}

int main() {
    int n;
    printf("请输入一个整数 n：");
    scanf("%d", &n);
    
    if (n < 0) {
        printf("输入的数必须为非负整数。\n");
    } else {
        int result = factorial(n);
        printf("%d 的阶乘是 %d\n", n, result);
    }
    
    return 0;
}

我们把n的值加大到10的时候那么我们需要算10！=9* 8！然后8！=8*7，一直都会有这种子问题下去这样会非常的浪费空间稍微大一点就会崩掉，如果采用迭代的方式来算n！，直接循环n次累乘很快变可以出现答案

1.2 算法的复杂度

算法在编写成可执行程序后，运行时需要耗费时间资源和空间 ( 内存 ) 资源。因此 衡量一个算法的好坏，一般

是从时间和空间两个维度来衡量的 ，即时间复杂度和空间复杂度。

时间复杂度主要衡量一个算法的运行快慢，而空间复杂度主要衡量一个算法运行所需要的额外空间 。在计算

机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计

算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。

1.3 复杂度在校招中的考察

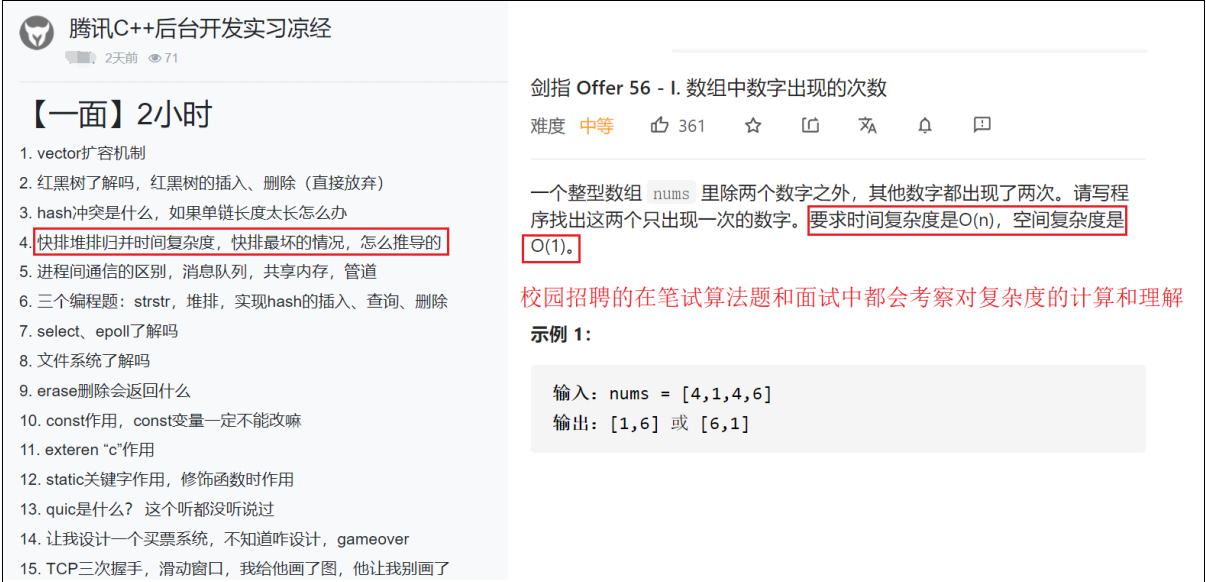
2.时间复杂度

2.1 时间复杂度的概念

时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个函数 ，它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法 的时间复杂度。

即：找到某条基本语句与问题规模 N 之间的数学表达式，就是算出了该算法的时间复杂度。

// 请计算一下Func1中++count语句总共执行了多少次？
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
     for (int j = 0; j < N ; ++ j)
     {
         ++count;
     }
}
for (int k = 0; k < 2 * N ; ++ k)
{
     ++count;
}
    int M = 10;
    while (M--)
{
     ++count;
}
    printf("%d\n", count);
}

Func1 执行的基本操作次数：

N = 10 F(N) = 130
N = 100 F(N) = 10210
N = 1000 F(N) = 1002010

实际中我们计算时间复杂度时，我们其实并不一定要计算精确的执行次数，而只需要 大概执行次数，那么这 里我们使用大 O 的渐进表示法。

在很多大学竞赛中很多算法都采用时间复杂度来区分一个选手的得分

例如下面是我们学校的一道竞赛题

一般会用很多数据去测你写的程序如果时间复杂度不达标就算写出了效果也拿不到满分

就那这题举例如果我们写了一个算斐波那契的函数然后再去双重循环累加，那么恭喜你喜提百分之20的巨额分数

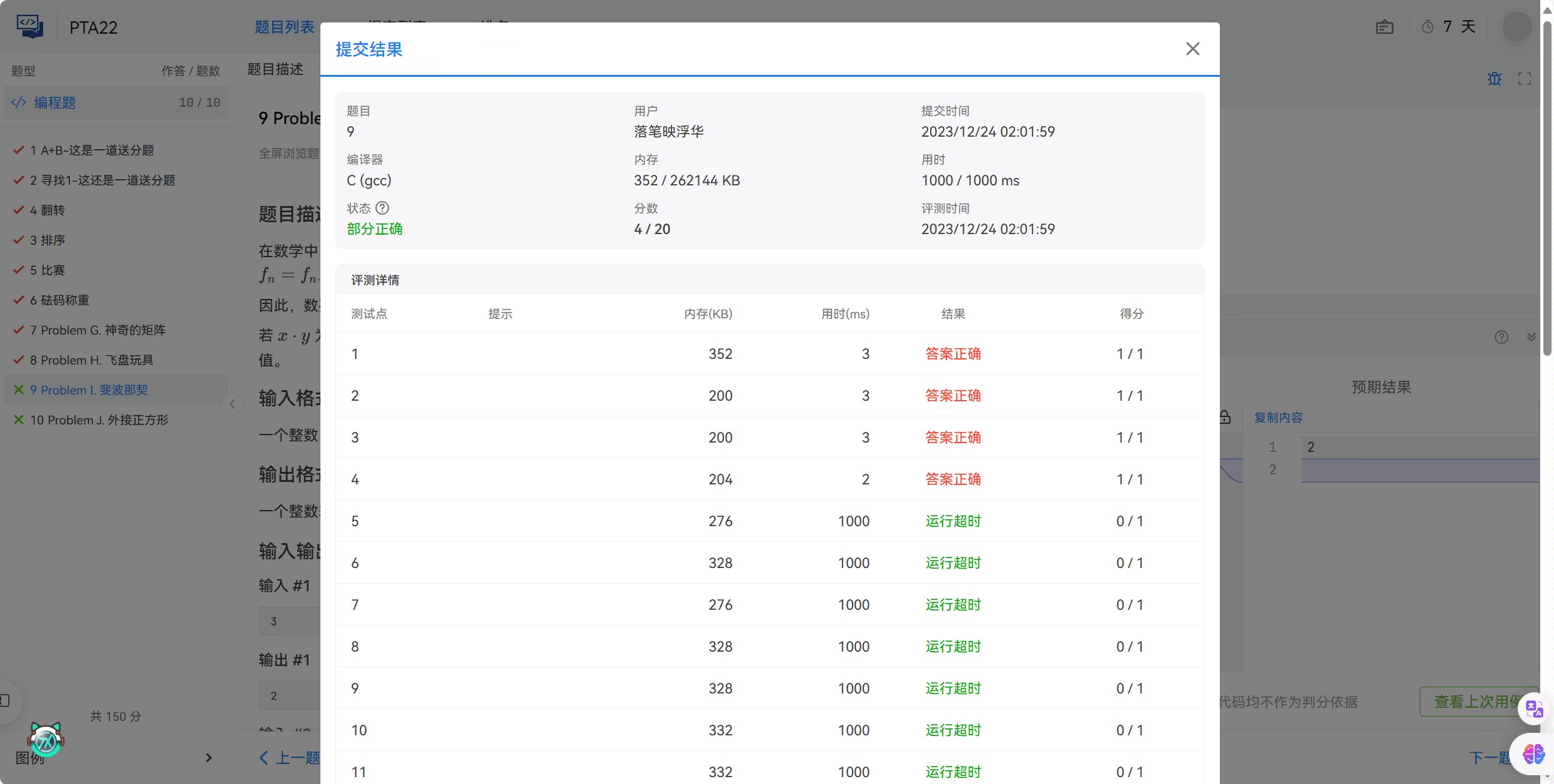
满分代码：

2.2 大O的渐进表示法

大 O 符号（ Big O notation ）：是用于描述函数渐进行为的数学符号。

推导大 O 阶方法：

1 、用常数 1 取代运行时间中的所有加法常数。

2 、在修改后的运行次数函数中，只保留最高阶项。

3 、如果最高阶项存在且不是 1 ，则去除与这个项目相乘的常数。得到的结果就是大 O 阶。

使用大 O 的渐进表示法以后， Func1 的时间复杂度为

N = 10 F(N) = 100

N = 100 F(N) = 10000

N = 1000 F(N) = 1000000

通过上面我们会发现大 O 的渐进表示法 去掉了那些对结果影响不大的项 ，简洁明了的表示出了执行次数。

另外有些算法的时间复杂度存在最好、平均和最坏情况：

最坏情况：任意输入规模的最大运行次数 ( 上界 )

平均情况：任意输入规模的期望运行次数

最好情况：任意输入规模的最小运行次数 ( 下界 )

例如：在一个长度为 N 数组中搜索一个数据 x

最好情况： 1 次找到

最坏情况： N 次找到

平均情况： N/2 次找到

在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为 O(N)

2.3常见时间复杂度计算举例

实例 1 ：

// 计算Func2的时间复杂度？
void Func2(int N)
{
 int count = 0;
 for (int k = 0; k < 2 * N ; ++ k)
 {
 ++count;
 }
 int M = 10;
 while (M--)
 {
 ++count;
 }
 printf("%d\n", count);
}

实例 2:

// 计算Func3的时间复杂度？
void Func3(int N, int M)
{
 int count = 0;
 for (int k = 0; k < M; ++ k)
 {
     ++count;
 }
for (int k = 0; k < N ; ++ k)
 {
     ++count;
 }
     printf("%d\n", count);
}

实例 3:

// 计算Func4的时间复杂度？
void Func4(int N)
{
 int count = 0;
 for (int k = 0; k < 100; ++ k)
 {
     ++count;
 }
     printf("%d\n", count);
}

实例 4:

// 计算strchr的时间复杂度？
const char * strchr ( const char * str, int character );

实例5:

// 计算BubbleSort的时间复杂度？
void BubbleSort(int* a, int n)
{
 assert(a);
 for (size_t end = n; end > 0; --end)
 {
 int exchange = 0;
 for (size_t i = 1; i < end; ++i)
 {
     if (a[i-1] > a[i])
     {
         Swap(&a[i-1], &a[i]);
         exchange = 1;
     }
     }
        if (exchange == 0)
         break;
     }
}

实例 6:

// 计算BinarySearch的时间复杂度？
int BinarySearch(int* a, int n, int x)
{
     assert(a);
     int begin = 0;
     int end = n-1;
 // [begin, end]：begin和end是左闭右闭区间，因此有=号
while (begin <= end)
 {
     int mid = begin + ((end-begin)>>1);
     if (a[mid] < x)
         begin = mid+1;
     else if (a[mid] > x)
         end = mid-1;
     else
         return mid;
     }
 return -1;
}

实例 7:

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
{
 if(0 == N)
 return 1;
 
 return Fac(N-1)*N;
}

实例 8:

// 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N)
{
 if(N < 3)
 return 1;
 
 return Fib(N-1) + Fib(N-2);
}

实例答案及分析：

1. 实例 1 基本操作执行了 2N+10 次，通过推导大 O 阶方法知道，时间复杂度为 O(N)

2. 实例 2 基本操作执行了 M+N 次，有两个未知数 M 和 N ，时间复杂度为 O(N+M)

3. 实例 3 基本操作执行了 10 次，通过推导大 O 阶方法，时间复杂度为 O(1)

4. 实例 4 基本操作执行最好 1 次，最坏 N 次，时间复杂度一般看最坏，时间复杂度为 O(N)

5. 实例 5 基本操作执行最好 N 次，最坏执行了 (N*(N+1)/2 次，通过推导大 O 阶方法 + 时间复杂度一般看最

坏，时间复杂度为 O(N^2)

6. 实例 6 基本操作执行最好 1 次，最坏 O(logN) 次，时间复杂度为 O(logN) ps ： logN 在算法分析中表示是底

数为 2 ，对数为 N 。有些地方会写成 lgN 。（建议通过折纸查找的方式讲解 logN 是怎么计算出来的）

7. 实例 7 通过计算分析发现基本操作递归了 N 次，时间复杂度为 O(N) 。

8. 实例 8 通过计算分析发现基本操作递归了 2^N 次，时间复杂度为 O(2^N) 。（建议画图递归栈帧的二叉树

讲解）

3.空间复杂度

空间复杂度也是一个数学表达式，是对一个算法在运行过程中 临时占用存储空间大小的量度 。

空间复杂度不是程序占用了多少 bytes 的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。

空间复杂度计算规则基本跟实践复杂度类似，也使用大 O 渐进表示法 。

注意： 函数运行时所需要的栈空间 ( 存储参数、局部变量、一些寄存器信息等 ) 在编译期间已经确定好了，因 此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。

实例 1 ：

// 计算BubbleSort的空间复杂度？
void BubbleSort(int* a, int n)
{assert(a);
 for (size_t end = n; end > 0; --end)
 {
     int exchange = 0;
     for (size_t i = 1; i < end; ++i)
     {
         if (a[i-1] > a[i])
     {
         Swap(&a[i-1], &a[i]);
         exchange = 1;
     }
 }
     if (exchange == 0)
         break;
     }
}

实例 2 ：

// 计算Fibonacci的空间复杂度？
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
 if(n==0)
 return NULL;
 
 long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
 fibArray[0] = 0;
 fibArray[1] = 1;
 for (int i = 2; i <= n ; ++i)
 {
 fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
 }
 return fibArray;
}

实例 3 ：

// 计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N)
{
 if(N == 0)
 return 1;
 
 return Fac(N-1)*N;
}

实例答案及分析：

1. 实例 1 使用了常数个额外空间，所以空间复杂度为 O(1)

2. 实例 2 动态开辟了 N 个空间，空间复杂度为 O(N)

3. 实例 3 递归调用了 N 次，开辟了 N 个栈帧，每个栈帧使用了常数个空间。空间复杂度为 O(N)

4. 常见复杂度对比

一般算法常见的复杂度如下：

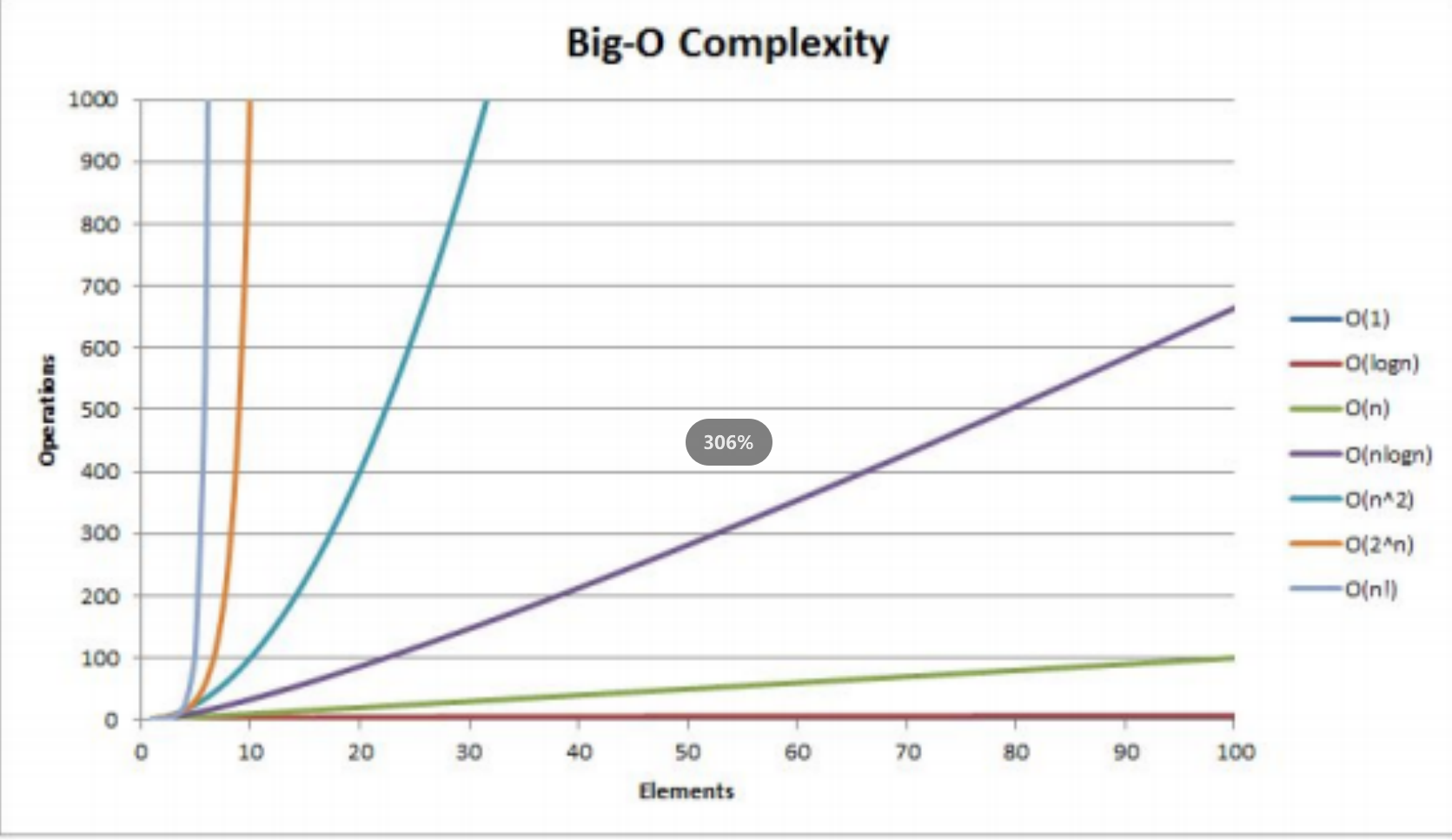
5. 复杂度的oj练习

3.1 消失的数字 OJ 链接： https://leetcode-cn.com/problems/missing-number-lcci /

面试题 17.04. 消失的数字 - 力扣（LeetCode）

思路1：把1-n的数累加到sum里面然后再遍历这个数组，用sum减去数组的每一个数最后就会剩下那个缺少的数

int missingNumber(int* nums, int numsSize){
    int sum=0;
    for(int i=0;i<=numsSize;i++)
    {
        sum=sum+i;
    }
       for(int i=0;i<numsSize;i++)
    {
        sum=sum-nums[i];
    }
    return sum;


}

但是这种方式需要考虑一种极端的情况就是sum值溢出的问题

思路2：这里需要理解一个概念 x^0=x x^x=0，这里先让x去和0-n的数^一变，因为相同异或的数已经是0了那么剩下的x的值就是缺少的那个值，因为成对出现的都会是0，这里把x定义为0，0^x=0

所以这里好观察那个单独的数是什么

int missingNumber(int* nums, int numsSize){
    int n=numsSize;
    int x=0;
    for(int i=0;i<=n;i++)
    {
        x=x^i;
    }
    for(int i=0;i<numsSize;i++)
    {
        x=x^nums[i];
    }
    return x;

}

3.2 旋转数组 OJ链接： 189. 轮转数组 - 力扣（LeetCode）

第一种时间复杂度是o(n^2)所以这道题就不考虑了，这道题时间过不去

思路2代码实现：

三段逆置法

void Reverse(int* array,int left, int right)
{
    while(left<right)
    {
        int temp=array[left];
        array[left]=array[right];
        array[right]=temp;
        left++;
        right--;
    }
}
void rotate(int* nums, int numsSize, int k) {
    k=k%numsSize;
    Reverse(nums,0,numsSize-k-1);
    Reverse(nums,numsSize-k,numsSize-1);
    Reverse(nums,0,numsSize-1);

}

这个时间复杂度是o（n）就可以过

思路3：

思路2如果提前没有做过，第一次做，基本不可能能直接现场推出来，一般人只能学习大佬留下来的方法

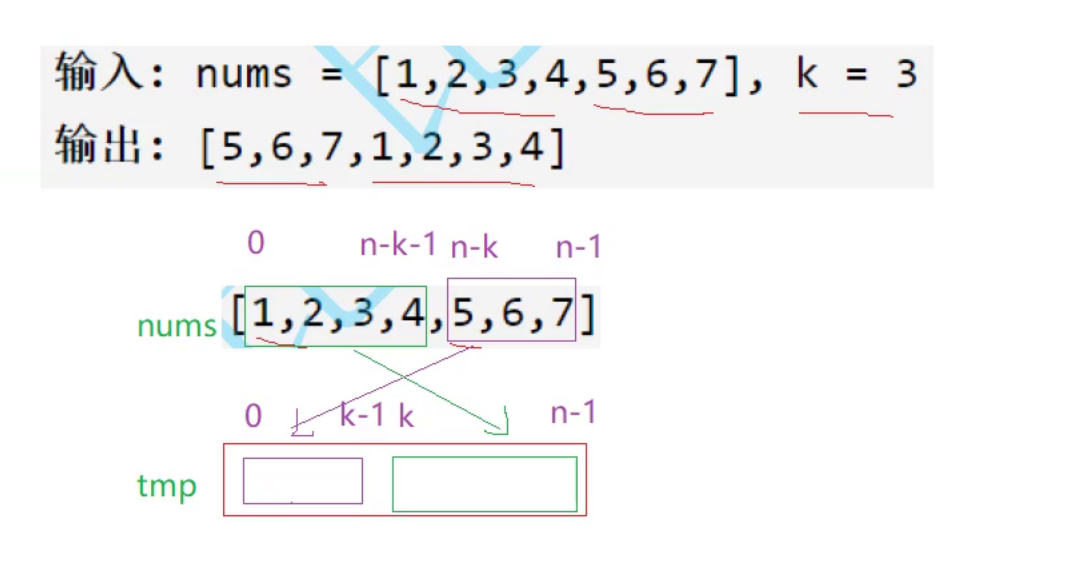
void rotate(int* nums, int numsSize, int k) {
    k=k%numsSize;
    int temp[numsSize];
    int n=numsSize;
    memcpy(temp,nums+n-k,sizeof(int)*k);
    memcpy(temp+k,nums,sizeof(int)*(n-k));
    memcpy(nums,temp,sizeof(int)*n);

}