1.1 二分查找模板
bool check(int x)
{
// 进行某些操作
}
// 二分查找函数
int binarySearch()
{
int l = 1, r = n; // 初始化左右边界
while (r - l > 1) // 当右边界与左边界相差大于1时
{
int mid = (l + r) >> 1; // 取中间位置
if (check(mid)) // 如果满足条件
r = mid; // 更新右边界为mid
else
l = mid; // 否则更新左边界为mid
}
if (check(l)) // 如果满足条件
return l; // 返回左边界值
else if (check(r)) // 如果满足条件
return r; // 返回右边界值
else
return -1; // 否则返回-1
}
-
例题
题目描述
小华被大林叫去砍树,他需要砍倒 m 米长的木材。现在,小华弄到了一个奇怪的伐木机。 伐木机工作过程如下:小华设置一个高度参数 h(米),伐木机升起一个巨大的锯片到高度 h, 并锯掉所有的树比 h 高的部分(当然,树木不高于 h 米的部分保持不变)。小华就得到树木被锯下的部分。 例如,如果一行树的高度分别为 20、15、10、15、10 和 17 米,小华把锯片升到 15米的高度,切割后树木剩下的高度将是 15、15、10和 15 米,而小华将从第 1 棵树得到 5 米, 从第 4 棵树得到 2 米,共得到 7 米木材。 小华非常关注生态保护,所以他不会砍掉过多的木材。这正是他为什么要尽可能高地设定伐木机锯片的原因。 现在请你帮助小华找到伐木机锯片的最大的整数高度 h,使得他能得到的木材至少为 m米。换句话说,如果再升高 1 米,则他将得不到 m 米木材。
输入格式
第 1 行 2 个整数 n和 m*, n* 表示树木的数量, m 表示需要的木材总长度。
第 2 行 n个整数,表示每棵树的高度,值均不超过 10的9次方。保证所有木材长度之和大于 m, 因此必然有解。输出格式
一行一个整数,表示砍树的最高高度。
样例
输入数据 1
5 20 4 42 40 26 46输出数据 1
36说明/提示
- 对于 30%30% 的数据:1≤n≤10,1≤m≤30。
- 对于 70%70% 的数据:1≤n≤1e3,1≤m≤1e4。
- 对于 100%100% 的数据:1≤n≤1e6,1≤m≤2×1e9。
-
代码
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N=1e6+10; ll a[N]; ll n,m; ll maxn=0; int check(ll x){ ll res=0; for(int i=1;i<=n;i++) if(a[i]>=x) res+=a[i]-x; return res>=m; } int main(){ cin>>n>>m; for(int i=1;i<=n;i++){ cin>>a[i]; maxn=max(maxn,a[i]); } ll l=1,r=maxn; while(r-l>1){ ll mid=(l+r)/2; if(check(mid)){ l=mid; } else{ r=mid; } } if(check(r)) cout<<r; else cout<<l; return 0; }
1.2 一维前缀和

- 代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10; // 定义常量N,表示数组长度的上限
int sum[N]; // 定义数组sum,用于存储前缀和
int main() {
int n, k, x;
cin >> n; // 输入数组长度
// 计算前缀和
for(int i = 1; i <= n; i++) {
cin >> x; // 输入数组元素
sum[i] = sum[i - 1] + x; // 计算前缀和并存储到数组sum中
}
cin >> k; // 输入查询次数k
while(k--) {
int l, r;
cin >> l >> r; // 输入查询区间[l,r]
// 输出区间和,利用前缀和数组sum进行快速计算
cout << sum[r] - sum[l - 1] << endl;
}
return 0;
}
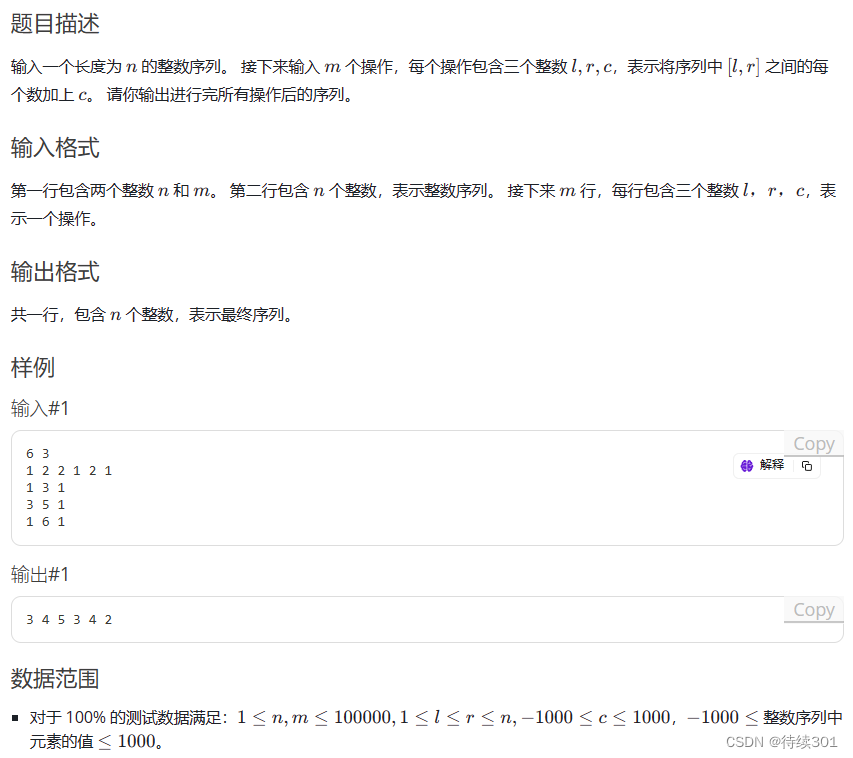
1.3 一维差分
#include<bits/stdc++.h>
using namespace std;
int n,m,a[100005],d[100005],sumd[100005];
int main()
{
cin>>n>>m;
int l,r,c;
for(int i=1;i<=n;i++)//存数据
{
cin>>a[i];
d[i]=a[i]-a[i-1];//记录差分数组
}
for(int i=1;i<=m;i++)//m次区间操作
{
cin>>l>>r>>c;
d[l]+=c;
d[r+1]-=c;
}
for(int i=1;i<=n;i++)//求最终的前缀和,即修改收后的a
{
sumd[i]=sumd[i-1]+d[i];
cout<<sumd[i]<<" ";
}
return 0;
}
-
例题
- 代码
#include<bits/stdc++.h> using namespace std; const int N = 1e5 + 10; int a[N]; //原数组 int d[N]; //差分数组 int s[N]; //原数组(修改后的) int main() { int n, m; cin >> n >> m; for(int i = 1; i <= n; i++) cin >> a[i]; //求差分数组 for(int i = 1; i <= n; i++) d[i] = a[i] - a[i-1]; //m次修改差分数组 for(int i = 1; i <= m; i++) { int l, r, x; cin >> l >> r >> x; d[l] += x, d[r + 1] -= x; } //对差分数组求前缀和,得到修改后的原数组 for(int i = 1; i <= n; i++) { s[i] = s[i - 1] + d[i]; cout << s[i] << " "; } return 0; }
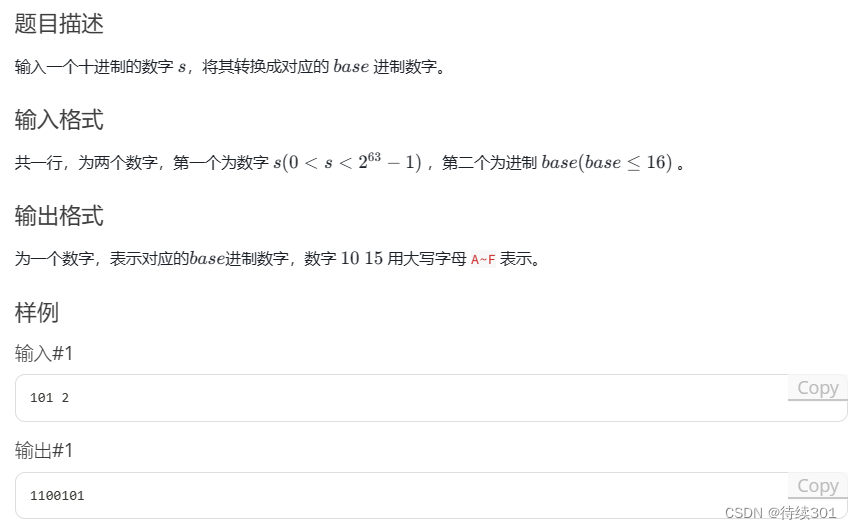
1.4 十进制转K进制 模板
-
例题
-
代码
#include <bits/stdc++.h> // 包含标准头文件 using namespace std; long long s, base; // 定义两个长整型变量,s 为要转换的数,base 为进制 string p = "0123456789ABCDEF"; // 定义字符串 p,存储 16 进制数的所有可能字符 string ans; // 定义字符串 ans,用于存储转换后的结果 int main() { cin >> s >> base; // 输入要转换的数 s 和进制 base while (s) { // 当 s 不为 0 时循环 ans.push_back(p[s % base]); // 将 s 对 base 取模的结果作为索引,将对应的字符添加到 ans 末尾 s /= base; // 将 s 除以 base,更新 s 的值 } reverse(ans.begin(), ans.end()); // 将 ans 反转,因为从末尾开始计算的结果需要反转才能得到正确的结果 cout << ans; // 输出转换后的结果 return 0; // 返回0,表示程序正常结束 }
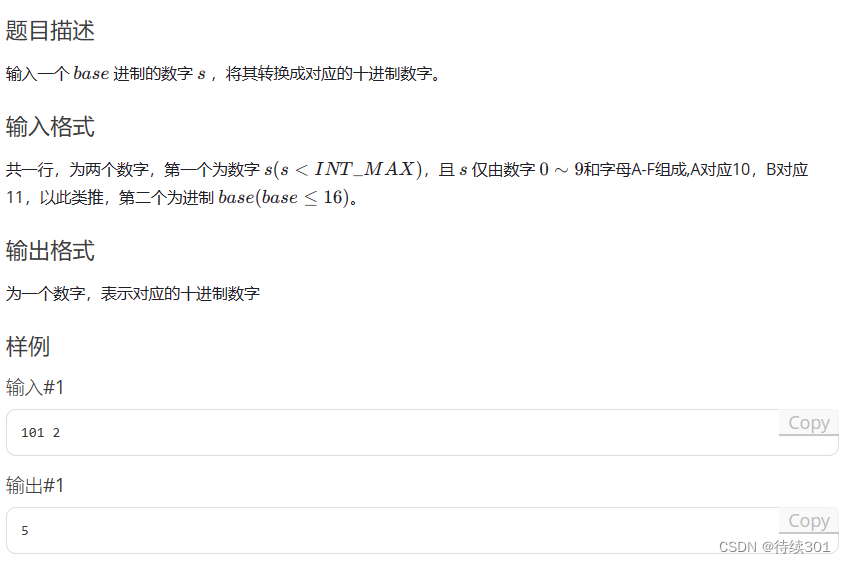
1.5 K进制转十进制 模板
- 例题
-
代码
#include<bits/stdc++.h> using namespace std; int main() { string s; long long base = 0, ans = 0, k = 0; // 初始化所有变量 // 输入字符串s和进制base cin >> s >> base; // 从字符串末尾开始遍历 for(int i = s.size() - 1; i >= 0; i--) { // 如果字符为大写字母 if(s[i] >= 'A') { ans += (s[i] - 'A' + 10) * pow(base, k++); // 更新结果 } else { ans += (s[i] - '0') * pow(base, k++); // 更新结果 } } // 输出结果 cout << ans; return 0; }
1.6 质数判断
#include<cstdio>
bool isprime(int num){
if(num==2)
return true;
if(num%2==0 || num<2)
return false;
else{
for(int i=3;i*i<=num;i+=2){
if(num%i==0){
return false;
}
}
return true;
}
}
int main(){
int x;
scanf("%d",&x);
if(isprime(x)){
printf("Yes");
}
else{
printf("No");
}
return 0;
}
1.7 最大公因数
-
C++有自带的 __gcd(a,b) 注意这里 gcd 前面 是两个 _ ,而且变量 和 数据类型必须相同,不能 是 int 型, 是 long long 型。
-
辗转相除法递归求解
int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }
1.8 最小公倍数

#include <bits/stdc++.h>
using namespace std;
// 求最大公约数
long long gcd(long long a, long long b) {
if (b == 0) {
return a;
}
return gcd(b, a % b);
}
int main() {
long long a, b;
// 输入两个数
cin >> a >> b;
// 计算最小公倍数,并输出结果
cout << a / gcd(a, b) * b; // 注意这里先乘再除可能会溢出,要先除再乘。
return 0;
}
![[目标检测] OCR: 文字检测、文字识别、text spotter](https://img-blog.csdnimg.cn/direct/91748be96c9d4ad9940de92ffa9ee9bf.png)