一. HMM
隐马尔可夫模型(Hidden Markov Model, HMM)是一种用于处理含有隐藏状态的序列数据的统计学习模型。通过建模隐藏状态之间的转移关系以及隐藏状态与观测数据的生成关系,HMM能够在仅观察到部分信息的情况下进行状态推理、概率计算、序列标注以及模型参数学习,从而服务于各种实际应用中的序列数据分析和预测任务。
所以,HMM特别适用于那些只能观察到部分信息(即观测序列),而系统的实际状态(即隐藏状态)无法直接观察的情况。
1.1 HMM中的基本概念
- 隐藏状态(Hidden States):系统的真实状态序列,通常表示为 S = S 1 , S 2 , . . . , S T S={S_1, S_2, ..., S_T} S=S1,S2,...,ST,其中每个状态 S t S_t St在某一时刻 t t t 独立地取值于一个离散状态集。这些状态是不可直接观察的,即我们不能直接看到系统处于哪个状态。
- 观测状态(Observation States):对应于隐藏状态序列的可观测数据序列,记为 O = O 1 , O 2 , . . . , O T O={O_1, O_2, ..., O_T} O=O1,O2,...,OT。每个观测 O t O_t Ot是隐藏状态 S t S_t St生成的,且与该时刻的隐藏状态相关联。
- 初始状态分布(Initial State Distribution):用 π π π表示,描述系统在起始时刻处于各个隐藏状态的概率分布,即 P ( S 1 = s ) P(S_1 = s) P(S1=s)。
- 状态转移概率(Transition Probabilities):用状态转移矩阵 A A A 表示,描述系统从一个隐藏状态转移到另一个隐藏状态的概率。 A i j A_{ij} Aij表示在任一时刻,系统从状态 i i i 转移到状态 j j j 的概率。
- 观测概率(Emission Probabilities):用观测概率矩阵 B B B 表示,给出在给定隐藏状态下生成某个观测值的概率。 B j ( k ) B_{j(k)} Bj(k) 表示在隐藏状态 j j j 下观测到符号 k k k 的概率。
1.2 HMM的运作机制
HMM的核心是通过已知的观测序列来推断隐藏状态序列以及模型参数。主要涉及以下三个基本问题:
- 概率计算问题(Evaluation Problem):给定一个HMM模型(M)和一个观测序列 O O O,计算该观测序列出现的概率 P ( O ∣ M ) P(O|M) P(O∣M)。
- 解码问题(Decoding Problem):给定一个HMM模型和一个观测序列 O O O,找出最有可能产生这个观测序列的隐藏状态序列,即求最大后验概率路径 a r g m a x S P ( S ∣ O , M ) argmax_S P(S|O, M) argmaxSP(S∣O,M)。
- 学习问题(Learning Problem):根据观测序列数据估计或学习HMM的参数(初始状态分布 π π π、状态转移矩阵 A A A 和观测概率矩阵 B B B),使得模型能够最好地解释给定的数据。
为了解决这些问题,HMM采用动态规划算法,如前向算法、后向算法、维特比算法(Viterbi algorithm)和Baum-Welch算法(也称EM算法)等,求解模型中给定观测序列下最可能的隐藏状态序列。
具体来说,维特比算法避免了对所有可能的隐藏状态序列进行枚举,而是通过动态规划实现了对最可能路径的高效搜索,时间复杂度为
O
(
T
×
N
2
)
O(T×N^2)
O(T×N2),其中
T
T
T 是观测序列长度,
N
N
N 是隐藏状态数量。
1.3 HMM中的先验概率和后验概率
先验概率在HMM中用于设定模型学习的起点或约束,而后验概率则是模型学习的结果,反映了在已知观测数据条件下对隐藏状态和模型参数的最可靠估计。在实际应用中,后验概率常用于状态解码(找到最可能的隐藏状态序列)、模型评估、参数调整以及后续的决策过程。
- 先验概率
- 模型参数的先验:在训练HMM时,如果采用贝叶斯方法,可以为模型的转移概率矩阵(状态间的转移概率)和发射概率矩阵(状态生成观测的概率)指定先验分布。这些先验分布反映了在观察数据之前对模型参数的主观信念或基于领域知识的猜测,有助于引导参数估计过程,尤其是在数据稀疏时避免过度拟合。
- 隐藏状态的先验:对于某个具体的HMM实例,在开始观测序列之前,每个隐藏状态被观察到的概率称为状态的先验概率。在模型初始化或无观测数据可用时,这些概率可以是均匀分布,即假设所有隐藏状态在开始时具有相同的可能性,也可以基于其他信息设定不同的初始分布。
- 后验概率
- 模型参数的后验:通过应用贝叶斯定理,结合先验分布和观测数据(似然函数),可以计算出模型参数的后验分布。这些后验概率反映了在观察到实际数据后,对模型参数的更新认知,是参数估计和模型推理的基础。
- 隐藏状态的后验:对于给定的观测序列,计算每个隐藏状态在生成该序列条件下的概率,这就是状态的后验概率。这是HMM中最核心的计算之一,通常通过前向-后向算法或维特比算法实现。
1.4 HMM的应用
在自然语言处理中,HMM常用于词性标注任务。隐藏状态代表词性类别(如名词、动词、形容词等),观测状态则是实际的单词。模型通过学习文本数据中的上下文信息来预测每个单词的最可能词性。
二. CRF
条件随机场(Conditional Random Field, CRF)是一种统计建模工具,主要用于处理序列数据的标注问题,如自然语言处理中的词性标注、命名实体识别、语块划分、语音识别的音素标注等任务。CRF是一种鉴别式(discriminative)概率模型,与生成式模型(如隐马尔可夫模型HMM)不同,它直接对观察数据进行建模以预测其对应的标签序列,而不是同时建模数据的生成过程。
2.1 CRF的概率计算
CRF是一种特殊的随机场,它是在给定一组观测序列(例如文本中的单词序列)的条件下,对另一组相关随机变量(例如每个单词的词性标签序列)建模。
对于给定的观测序列
X
X
X,CRF的目标是找到最可能的标签序列
Y
Y
Y,即求解
a
r
g
m
a
x
Y
P
(
Y
∣
X
)
argmax_Y P(Y|X)
argmaxYP(Y∣X)。这涉及到对所有可能的标签序列求和来计算归一化常数(分母),即所有路径的概率总和,实际应用中常采用动态规划算法(如维特比算法)有效地求解最优标签序列(分子)。
2.2 特征函数与线性链CRF:
CRF的概率模型通常通过定义一组特征函数
f
k
(
Y
,
X
)
f_k(Y,X)
fk(Y,X)来描述观测
X
X
X 和标签
Y
Y
Y 之间的关系。这些特征函数可以编码各种上下文信息,如词性标注中某个单词的上下文词性组合、生物序列中特定基序的出现等。
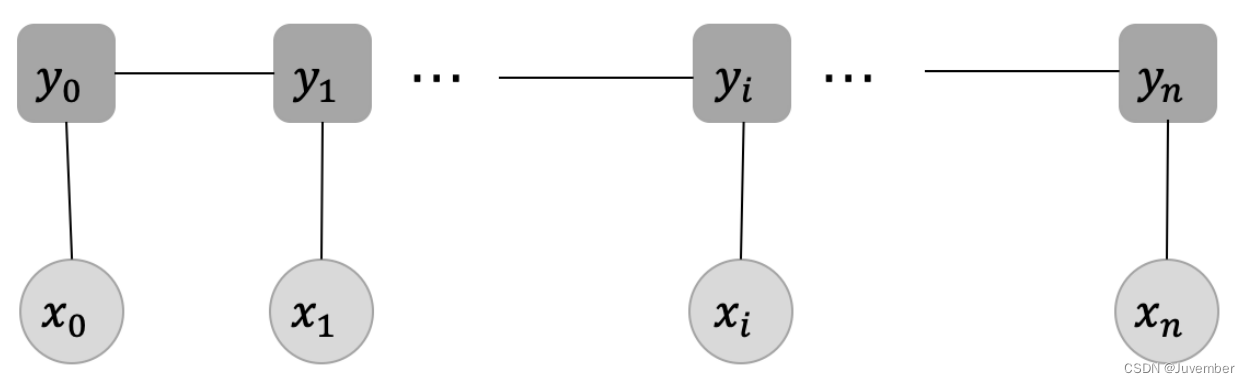
在最常用的线性链CRF中(如上图所示),特征函数通常依赖于当前位置 i i i 的标签 y i y_i yi、前一个位置 i − 1 i-1 i−1 的标签 y i − 1 y_{i-1} yi−1 以及与位置 i i i 相关的观测 x i x_i xi。其中,每个观测 x i x_i xi均对应着一个标签 y i y_i yi ,这一步对应的就是发射分数,它指示了当前的输入应该对应什么样的标签;而在每两个标签之间的连线则表示当前位置的标签向下一个位置的标签的一种转移,这就是状态转移分数。
三. CRF与HMM的区别
- 模型类型:HMM是生成式模型,它同时建模观测序列和隐藏状态序列(相当于标签序列)的联合分布 P ( X , Y ) P(X,Y) P(X,Y),然后通过贝叶斯规则推导条件概率 P ( Y ∣ X ) P(Y|X) P(Y∣X)。而CRF直接建模条件概率 P ( Y ∣ X ) P(Y|X) P(Y∣X),更专注于学习决策边界,通常能更好地利用观测数据的特性。
- 特征表达能力:HMM依赖于固定的转移概率和发射概率,而CRF通过特征函数可以灵活地捕获更复杂的观测与标签之间的关系,允许模型学习到更多的上下文信息。
- 参数学习:HMM通常使用期望最大化(EM)算法进行参数估计,而CRF通常采用极大似然估计或正则化的极大似然估计,配合梯度上升、拟牛顿法等优化算法求解参数。