等额本息贷款和等额本金贷款的月供应该怎么算?
从一个例子开始,假设我要从银行贷款36万(即,本金),银行给出的贷款年利率是12%(月利率为年利率除以12),贷款半年(6个月),按月还款,分6期还完。 问分别按照等额本息和等额本金的贷款方式去贷款,每个月应该还多少钱?
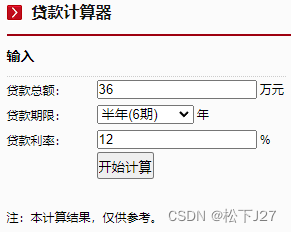
等额本息的计算结果:

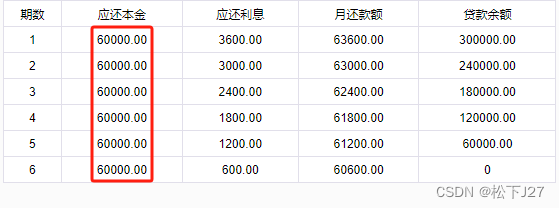
等额本金的计算结果:
计算器给出的结果共分5列,其中:
第一列表示期数,本例中存款半年,共分6期。
第二列表示每月所还贷款中本金所占的部分,本金就是贷款的原始资金。
第三列表示每月所还贷款中利息所占的部分,利息就是你找银行借钱要付给银行的酬劳,毕竟银行不可能白白借给你钱。你除了要还给银行最开始借的那部分钱,即,本金,还要再多给银行一部分额外的钱,即,利息。
第四列为每月所还的贷款,他等于第二列(本金)和第三列(利息)的和。
第五列是你每月还欠银行的钱。可见,不管是采用那种贷款的方式去还贷,还到第六个月的时候欠银行的钱都是0了。
什么是等额本息,为什么叫等额本息?

注意看图中我用红色方框框出来的部分,这一列中每个月的还款金额是相同的。这是等额本息贷款的特点,也就是每个月连本带利息还给银行的钱一样多。
为什么叫等额本金?
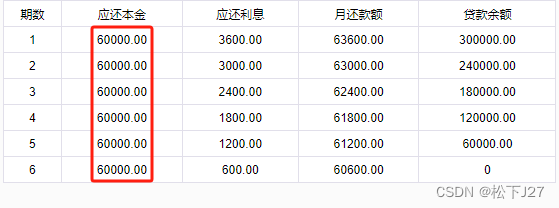
与等额本息不同的是,等额本金每月还款的金额是变动了,第一个月最高,最后一个月最少。但每个月的还款中,所还本金的数目相同(图中红色方框所框出来的部分),故而,这种还款的计息方式被称为等额本金。
等额本金每个月的月供是如何计算的?
等额本金还贷的本金和利息是分开单独计算的。
1,就本金而言,因为等额本金每个月的所还得金额相同。因此,我们先计算每个月所要还得本金:
36万/6=6万
得出,每月还款中所还本金得数额为6万。这和计算器得到得结果相同。

2,利息
第一个月,我总共欠银行36万,月利率为12%/12=1%。因此,第一个月我要付给银行的利息是:
36万*1%=3600元
第二月,因为我第一个月还了6万的本金,因此,我总共欠银行的钱变成了30万。第二个月我要付给银行的利息是基于当前的欠款总额计算的,即:
30万*1%=3000元
第三月,我第二个月又还了6万的本金,因此,我总共欠银行的钱变成了24万。我要付给银行的利息也是基于当前的欠款总额计算的,即:
24万*1%=2400元
......
依此类推,到了第六个月,我前面已经还了30万本金,这时我只欠银行6万了。这时我需要还的利息是:
6万*1%=600元
总共的利息是:
3600+3000+2400+1800+1200+600=(3600+600)/2*6= 12600元
连本带利整个还款的总额为总本金加总利息:
360000+ 12600=372600元
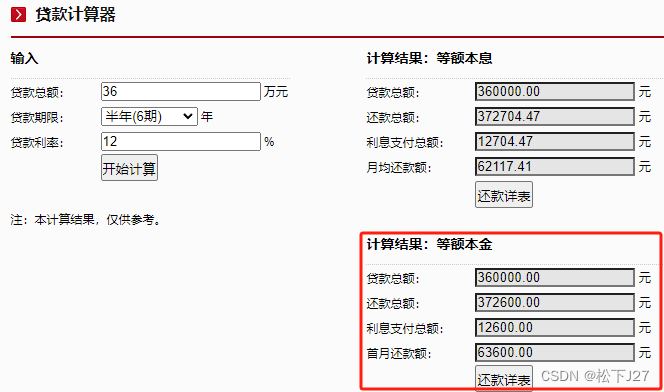
这和贷款计算器给出的结果是吻合的:
等额本息每个月的月供是如何计算的?
等额本息的计算要基于等额本息的还款特性,也就是每个月所还欠款是等额的。但一开始我们是不知道具体数额的,这和等额本金不同。
设:
每月还款的金额(本金+利息)为A。截止到每个月欠款的总额为。
则:
第一个月欠款总额为,贷款总本金。因为,到目前为止,既没有开始还款,也没有产生任何借贷利息。
从第二个月开始还款并开始按月计算贷款利息。欠款总额为,第一个月的欠款总额加第一个月的利息,再减去第一个月的还款。
第三个月欠款总额为,第二个月的欠款总额加第二个月的利息,再减去第二个月的还款。
......
依此类推,第六个月的欠款总额为
且,第六个月正好把欠款还完,因此, 。
逐一回代方程中变量得到:
把上式重新排列一下,得到:
括号中是一个几何级数(geometric series),也被称之为等比数列。根据等比数列的求和公式,首项,公比,项数分别为:
代入求和公式:
把这个结果回代到方程中的后半部分:
又因为,得到:
最后代入本金,得到:
连本带利的还款的总额为,月供乘以总的还款月数:
62117.41*6=372704.46元
所还总利息为,还款总额减去本金:
372704.46-360000=12704.46
这和贷款计算器给出的结果是吻合的,需要注意的是等额本息所支付的利息要略高于等额本金的利息。

最后,为了便于计算,我们给出等额本息贷款方式计算月供的通式 :
其中:
1,P表示本金,principal。
2,,表示月利率,等于年利率除以12。例如,在本例中为0.12/12=0.01。
3,n表示贷款周期,如果按照月利率算就等于贷款的总年数乘以12。例如,在本例中就是0.5(半年)*12。
为什么会有房奴的说法?
在上面的例子中,贷款金额不算高,且贷款时间很短(虽然例子中的利息确实挺高的)。但如果你要是选择在北上广买一套房,且按照贷款30年来算,还款时贷款人所支付的总利息会是多少呢?
比如说,我们付完首付后,需要向银行借的钱分别是100万,500万或1000万,统一按照贷款30年,贷款年利率为4.5%算。
贷款100万:

贷款100万,不论是用那种方式还款,平均下来要付70多万的利息,且等额本息要比等额本金多还大概15万。
贷款500万:

贷款500万,平均下来要付350多万的利息,且等额本息要比等额本金多还大概74万。
贷款1000万:

贷款1000万,平均下来要付700多万的利息,且等额本息要比等额本金多还大概150万。
这样看来,你如果你贷款的金额越大,切贷款30年(即,360个月)的话,你要还的利息基本上都已经接近是大半套房子的钱了! 这就是为什么说有些买房的人会说自己是房奴,毕竟买个房子要多付那么多的利息钱,还款的周期还特别长。
(全文完)
作者 --- 松下J27
格言摘抄:
真实是一切的开始!
参考文献(鸣谢):
1,https://www.youtube.com/watch?v=T6FBfNpiBYw
2,贷款计算器 - 首页 - 广发银行

(配图与本文无关)
版权声明:文中的部分图片,文字或者其他素材,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27